MN07: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
||
| (Nie pokazano 11 wersji utworzonych przez 2 użytkowników) | |||
| Linia 66: | Linia 66: | ||
wartością przybliżoną uzyskaną np. algorytmem eliminacji Gaussa, będziemy | wartością przybliżoną uzyskaną np. algorytmem eliminacji Gaussa, będziemy | ||
posługiwać się normami wektorów | posługiwać się normami wektorów | ||
<math> | <math>x = (x_j)_{j=1}^n\in R^n</math> | ||
i macierzy <math> | i macierzy <math>A = (a_{i,j})_{i,j=1}^n \in R^{n\times n}</math>. | ||
Najczęściej używanymi normami wektorowymi będą | Najczęściej używanymi normami wektorowymi będą | ||
<strong>normy <math> | <strong>normy <math>p</math>-te</strong>, | ||
<center><math> | <center><math>\| x\|\,=\,\| x\|_p\,=\, | ||
\left(\sum_{j=1}^n |x_j|^p\right)^{1/p}, | \left(\sum_{j=1}^n |x_j|^p\right)^{1/p}, | ||
\qquad 1\le p< +\infty | \qquad 1\le p< +\infty</math>,</center> | ||
</math></center> | |||
oraz | oraz | ||
<center><math> | <center><math>\| x\|_\infty\,=\,\lim_{p\to +\infty}\| x\|_p\,=\, | ||
\max_{1\le j\le n}|x_j|. | \max_{1\le j\le n}|x_j|. | ||
</math></center> | </math></center> | ||
W szczególności, norma <math> | W szczególności, norma <math>||\cdot||_2</math> jest dobrze nam znaną normą euklidesową wektora. | ||
[[Image:MNball1.png|thumb|300px|center|Kula jednostkowa w normie <math> | [[Image:MNball1.png|thumb|300px|center|Kula jednostkowa w normie <math>||\cdot||_1</math> w <math>R^2</math>]] | ||
[[Image:MNball2.png|thumb|300px|center|Kula jednostkowa w normie <math> | [[Image:MNball2.png|thumb|300px|center|Kula jednostkowa w normie <math>||\cdot||_2</math> w <math>R^2</math>]] | ||
[[Image:MNballinf.png|thumb|300px|center|Kula jednostkowa w normie <math> | [[Image:MNballinf.png|thumb|300px|center|Kula jednostkowa w normie <math>||\cdot||_\infty</math> w <math>R^2</math>]] | ||
Normą macierzową jest norma Frobeniusa | Normą macierzową jest norma Frobeniusa | ||
<center><math> | <center><math>\|A\|_F\,=\,\sqrt{\sum_{i,j=1}^n |a_{i,j}|^2}</math>,</center> | ||
</math></center> | |||
a także <strong>normy indukowane</strong> przez normy wektorowe (np. przez | a także <strong>normy indukowane</strong> przez normy wektorowe (np. przez | ||
normy <math> | normy <math>p</math>-te) | ||
<center><math> | <center><math>\|A\|\,=\,\sup_{x\ne 0}\frac{\|A x\|}{\| x\|}\,=\, | ||
\sup_{\|x\|=1}\|A x\| | \sup_{\|x\|=1}\|A x\|</math></center> | ||
</math></center> | |||
Jeśli norma macierzowa jest indukowana przez normę wektorową, | Jeśli norma macierzowa jest indukowana przez normę wektorową, | ||
to dla dowolnego wektora mamy | to dla dowolnego wektora mamy | ||
<center><math> | <center><math>\|A x\|\,\le\,\|A\|\| x\|. | ||
</math></center> | </math></center> | ||
Przypomnijmy, że w przestrzeniach liniowych skończenie wymiarowych | Przypomnijmy, że w przestrzeniach liniowych skończenie wymiarowych | ||
(a więc także w <math> | (a więc także w <math>R^n</math> i w przestrzeni macierzy wymiaru <math>n\times n</math>) | ||
każde dwie normy są równoważne. To znaczy, że jeśli mamy dwie | każde dwie normy są równoważne. To znaczy, że jeśli mamy dwie | ||
normy <math> | normy <math>\|\cdot\|</math> i <math>\|\cdot\|'</math> w przestrzeni skończenie wymiarowej | ||
<math> | <math>X</math>, to istnieją stałe <math>0<K_1\le K_2<\infty</math> takie, że | ||
<center><math> | <center><math>K_1\,\|x\|\,\le\,\|x\|'\,\le\,K_2\,\|x\|,\qquad\forall x\in X</math></center> | ||
</math></center> | |||
W szczególności dla <math> | W szczególności dla <math>x\in R^n</math> mamy | ||
<center><math>\ | <center><math>\begin{align} \| x\|_\infty &\le & \| x\|_1\,\le\, | ||
n\,\| x\|_\infty, \\ | n\,\| x\|_\infty, \\ | ||
\| x\|_\infty &\le & \| x\|_2\,\le\, | \| x\|_\infty &\le & \| x\|_2\,\le\, | ||
| Linia 123: | Linia 119: | ||
\frac 1{\sqrt n}\,\| x\|_1 &\le & \| x\|_2\,\le\, | \frac 1{\sqrt n}\,\| x\|_1 &\le & \| x\|_2\,\le\, | ||
\| x\|_1, | \| x\|_1, | ||
\ | \end{align}</math></center> | ||
a dla <math> | a dla <math>A=(a_{i,j})_{i,j=1}^n</math> mamy | ||
<center><math> | <center><math> | ||
\|A\|_2\, \le\, \|\,|A|\,\|_2 \,\le\, \|A\|_E | \|A\|_2\, \le\, \|\,|A|\,\|_2 \,\le\, \|A\|_E | ||
\,\le\, \sqrt n\, \|A\|_2 | \,\le\, \sqrt n\, \|A\|_2</math>,</center> | ||
</math></center> | |||
gdzie <math> | gdzie <math>|A|=(|a_{i,j}|)_{i,j=1}^n</math>. | ||
Dla macierzy | Dla macierzy | ||
<math> | <math>A=(a_{i,j})_{i.j=1}^n\in R^{n\times n}</math> mamy | ||
<center><math> | <center><math>\|A\|_\infty \,=\, \max_{1\le i\le n}\sum_{j=1}^n |a_{i,j}| | ||
</math></center> | </math></center> | ||
oraz | oraz | ||
<center><math> | <center><math>\|A\|_1 \,=\, \|A^T\|_\infty \,=\, | ||
\max_{1\le j\le n}\sum_{i=1}^n |a_{i,j}| | \max_{1\le j\le n}\sum_{i=1}^n |a_{i,j}|</math></center> | ||
</math></center> | |||
Dowód tego faktu zostawiamy jako [[MN07LAB|ćwiczenie]]. | Dowód tego faktu zostawiamy jako [[MN07LAB|ćwiczenie]]. | ||
| Linia 151: | Linia 145: | ||
Wyprowadzimy teraz wynik świadczący o tym, jak zaburzenie względne danych | Wyprowadzimy teraz wynik świadczący o tym, jak zaburzenie względne danych | ||
przenosi się na błąd względny wyniku rozwiązania <math> | przenosi się na błąd względny wyniku rozwiązania <math>x^*</math> układu równań liniowych <math>Ax=b</math>. | ||
{{twierdzenie|O uwarunkowaniu układu równań|O uwarunkowaniu układu równań| | {{twierdzenie|O uwarunkowaniu układu równań|O uwarunkowaniu układu równań| | ||
Niech <math> | Niech <math>E</math> i <math>e</math> będą zaburzeniami | ||
odpowiednio macierzy <math> | odpowiednio macierzy <math>A</math> i wektora <math>b</math> na poziomie względnym <math>\epsilon</math>, tzn. | ||
<center><math> | <center><math>\frac{\|E\|}{\|A\|} \,\le\,\epsilon \qquad \mbox{i} \qquad \frac{\|e\|}{\|b\|} \,\le\,\epsilon</math></center> | ||
</math></center> | |||
Jeśli | Jeśli | ||
<center><math> | <center><math>\epsilon\cdot \mbox{cond} (A)\,<\,1</math>,</center> | ||
</math></center> | |||
to układ zaburzony <math> | to układ zaburzony <math>(A+E) x=( b+ e)</math> ma jednoznaczne | ||
rozwiązanie <math> | rozwiązanie <math>z^*</math> spełniające | ||
<center><math> | <center><math>\frac{\| z^*- x^*\|}{\| x^*\|} \; \le \; \frac{2\, \mbox{cond} (A)}{1-\epsilon \mbox{cond} (A)} \epsilon</math>,</center> | ||
</math></center> | |||
gdzie definiujemy <strong>współczynnik uwarunkowania układu</strong> | gdzie definiujemy <strong>współczynnik uwarunkowania układu</strong> | ||
<center><math> | <center><math>\mbox{cond} (A) = ||A||\cdot ||A^{-1}||</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 181: | Linia 171: | ||
Zauważmy najpierw, że zachodzi | Zauważmy najpierw, że zachodzi | ||
{{lemat|Neumanna o otwartości zbioru macierzy odwracalnych|Neumanna o otwartości zbioru macierzy odwracalnych| | |||
{{lemat| | |||
Jeśli <math> | Jeśli <math>F</math> jest macierzą | ||
taką, że <math> | taką, że <math>\|F\|<1</math>, to macierz <math>(I-F)</math> jest nieosobliwa oraz | ||
<center><math> | <center><math>\| (I-F)^{-1} \|\,\le\,\frac{1}{1-\|F\|}</math></center> | ||
</math></center> | |||
}} | }} | ||
{{dowod||| | {{dowod||| | ||
Rzeczywiście, gdyby <math> | Rzeczywiście, gdyby <math>(I-F)</math> była osobliwa, to istniałby niezerowy | ||
wektor <math> | wektor <math>x</math> taki, że <math>(I-F) x=0</math>, co implikuje | ||
<math> | <math>\|F x\|/\| x\|=1</math> i w konsekwencji <math>\|F\|\ge 1</math>. Aby | ||
pokazać oszacowanie normy macierzy <math> | pokazać oszacowanie normy macierzy <math>(I-F)^{-1}</math> zauważmy, że | ||
<center><math>\ | <center><math>\begin{align} 1 &= \|I\|\,=\,\|(I-F)(I-F)^{-1}\| \\ &\ge & | ||
\|(I-F)^{-1}\|\,-\,\|F\|\,\|(I-F)^{-1}\| \\ | \|(I-F)^{-1}\|\,-\,\|F\|\,\|(I-F)^{-1}\| \\ | ||
&= (1-\|F\|)\,\|(I-F)^{-1}\|, | &= (1-\|F\|)\,\|(I-F)^{-1}\|, | ||
\ | \end{align}</math></center> | ||
skąd już wynika dowodzona nierówność. | skąd już wynika dowodzona nierówność. | ||
| Linia 209: | Linia 196: | ||
{{dowod|twierdzenia o uwarunkowaniu|twierdzenia o uwarunkowaniu| | {{dowod|twierdzenia o uwarunkowaniu|twierdzenia o uwarunkowaniu| | ||
Po podstawieniu <math> | Po podstawieniu <math>F=-A^{-1}E</math> mamy teraz | ||
<center><math> | <center><math>\|F\|\,\le\,\|A^{-1}\|\,\|E\|\,\le\,\epsilon\|A\|\,\|A^{-1}\|\,<\,1</math>,</center> | ||
</math></center> | |||
co wobec równości <math> | co wobec równości <math>A+E=A(I+A^{-1}E)</math> daje, że macierz <math>(A+E)</math> | ||
jest nieosobliwa i układ zaburzony ma jednoznaczne rozwiązanie | jest nieosobliwa i układ zaburzony ma jednoznaczne rozwiązanie | ||
<math> | <math>z^*</math>. Przedstawmy to rozwiązanie w postaci | ||
<math> | <math>z^*= x^*+( z^*- x^*)</math>. Rozpisując układ | ||
zaburzony i wykorzystując równość <math> | zaburzony i wykorzystując równość <math>A x^*= b</math> otrzymujemy, | ||
że <math> | że <math>(A+E)( z^*- x^*)= e\,-\,E x^*</math>, czyli | ||
<center><math> | <center><math>z^*- x^* \,=\, (I+A^{-1}E)^{-1}A^{-1}( e-E x^*)</math>,</center> | ||
</math></center> | |||
a stąd | a stąd | ||
<center><math>\ | <center><math>\begin{align} \| z^*- x^*\| &\le & \|(I+A^{-1}E)^{-1}\|\,\|A^{-1}\| \, | ||
(\| e\|+\|E\|\,\| x^*\| \\ | (\| e\|+\|E\|\,\| x^*\| \\ | ||
&\le & \frac{\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} | &\le & \frac{\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} | ||
| Linia 232: | Linia 217: | ||
&\le & \frac{\|A\|\,\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} | &\le & \frac{\|A\|\,\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} | ||
2\epsilon\cdot\| x^*\|, | 2\epsilon\cdot\| x^*\|, | ||
\ | \end{align}</math></center> | ||
co kończy dowód. | co kończy dowód. | ||
}} | }} | ||
Gdy więc np. <math> | Gdy więc np. <math>\epsilon \mbox{cond} (A) \leq \frac{1}{2}</math>, [[#O uwarunkowaniu układu równań|oszacowanie błędu rozwiązania układu zaburzonego]] możemy | ||
zastąpić czytelniejszym (choć mniej precyzyjnym) | zastąpić czytelniejszym (choć mniej precyzyjnym) | ||
<center><math> | <center><math>\frac{\| z^*- x^*\|}{\| x^*\|} \leq 4 \, \mbox{cond} (A) \, \epsilon</math></center> | ||
</math></center> | |||
Octave i MATLAB mają wbudowane funkcje wyznaczające normy wektorów i macierzy | Octave i MATLAB mają wbudowane funkcje wyznaczające normy wektorów i macierzy | ||
| Linia 253: | Linia 237: | ||
a także funkcje wyznaczające uwarunkowanie macierzy, przy czym Octave liczy | a także funkcje wyznaczające uwarunkowanie macierzy, przy czym Octave liczy | ||
tylko uwarunkowanie w normie <math> | tylko uwarunkowanie w normie <math>||\cdot||_2</math>: | ||
<div style="margin: 1em; padding:1em; color: #006; background-color:#fcfcfc;"><pre>cond(A) | <div style="margin: 1em; padding:1em; color: #006; background-color:#fcfcfc;"><pre>cond(A) | ||
| Linia 263: | Linia 247: | ||
macierze, których uwarunkowanie może być patologicznie duże (np. takie macierze | macierze, których uwarunkowanie może być patologicznie duże (np. takie macierze | ||
są chlebem powszednim osób rozwiązujących równania różniczkowe). | są chlebem powszednim osób rozwiązujących równania różniczkowe). | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
| Linia 270: | Linia 252: | ||
<div class="solution" style="margin-left,margin-right:3em;"> | <div class="solution" style="margin-left,margin-right:3em;"> | ||
Przykładem macierzy o uwarunkowaniu wyjątkowo szybko rosnącym z wymiarem jest m.in. <strong>macierz Hilberta</strong> <math>H_N = (h_{ij})_{i,j=1}^N</math>, gdzie | |||
<center><math> | <center><math> | ||
h_{ij} = \frac{1}{i+j-1} | h_{ij} = \frac{1}{i+j-1}</math></center> | ||
</math></center> | |||
[[Image:MNhilbertmatrix.png|thumb|550px|center|Macierz Hilberta wymiaru 25. Kolor odpowiada rzędowi wielkości elementu macierzy, dokładniej, <math> | [[Image:MNhilbertmatrix.png|thumb|550px|center|Macierz Hilberta wymiaru 25. Kolor odpowiada rzędowi wielkości elementu macierzy, dokładniej, <math>\log(h_{ij})</math>. Jak widzisz, większość elementów tej macierzy jest równa prawie zero, a więc w konsekwencji kolumny macierzy są prawie liniowo zależne. ]] | ||
Taką macierz możemy wygenerować w Octave komendą <code style="color: #006">hilb(N)</code>. Jest to bardzo specyficzna macierz, co m.in. przejawia się tym, że uwarunkowanie macierzy Hilberta rośnie eksponencjalnie z <math> | Taką macierz możemy wygenerować w Octave komendą <code style="color: #006">hilb(N)</code>. Jest to bardzo specyficzna macierz, co m.in. przejawia się tym, że uwarunkowanie macierzy Hilberta rośnie eksponencjalnie z <math>N</math>, <math>\mbox{cond} (H_N) \approx O(e^{3.5N})</math>: | ||
<div style="font-family: monospace; white-space: pre; border-style: dashed; border-width: thin; border-color: black; margin: 1em; padding:1em; color: #444; background-color:#fdfdfd;"><nowiki>octave:2> cond(hilb(5)) | <div style="font-family: monospace; white-space: pre; border-style: dashed; border-width: thin; border-color: black; margin: 1em; padding:1em; color: #444; background-color:#fdfdfd;"><realnowiki><realnowiki><nowiki>octave:2> cond(hilb(5)) | ||
ans = 4.7661e+05 | ans = 4.7661e+05 | ||
octave:3> cond(hilb(10)) | octave:3> cond(hilb(10)) | ||
| Linia 287: | Linia 268: | ||
octave:5> cond(hilb(20)) | octave:5> cond(hilb(20)) | ||
ans = 7.1209e+19 | ans = 7.1209e+19 | ||
</nowiki></div> | </nowiki></realnowiki></realnowiki></div> | ||
</div></div> | </div></div> | ||
| Linia 299: | Linia 280: | ||
Algorytm eliminacji Gaussa z wyborem elementu głównego w kolumnie, zrealizowany | Algorytm eliminacji Gaussa z wyborem elementu głównego w kolumnie, zrealizowany | ||
w arytmetyce <math> | w arytmetyce <math>fl_\nu</math>, | ||
<center><math> | wyznacza <math>\widetilde{x}</math> taki, że <math>\widetilde{x}</math> jest <strong>dokładnym</strong> rozwiązaniem zadania zaburzonego | ||
</math></center> | |||
<center><math>\widetilde{A}\widetilde{x} = b</math>,</center> | |||
przy czym | przy czym | ||
<center><math> | <center><math>\frac{||A-\widetilde{A}||_\infty}{||A||_\infty} \leq K \, N^3 \, \rho_N \, \nu</math>,</center> | ||
</math></center> | |||
dla pewnej niedużej stałej <math>K = O(1)</math>. <strong>Wskaźnik wzrostu</strong> <math>\rho_N</math> definiujemy tutaj jako | |||
<center><math>\rho_N = \frac{\max_{i,j}|\widetilde{u}_{ij}|}{\max_{i,j} |a_{ij}|}</math>,</center> | |||
gdzie <math> | gdzie <math>\widetilde{L}</math> i <math>\widetilde{U}</math> są numerycznie wyznaczonymi czynnikami rozkładu PA<math>=</math>LU. | ||
}} | }} | ||
Jak widzimy, kluczowe dla numerycznej poprawności jest oszacowanie ''wskaźnika wzrostu'' <math> | Jak widzimy, kluczowe dla numerycznej poprawności jest oszacowanie ''wskaźnika wzrostu'' <math>\rho_N</math>. Okazuje się, co wiedział już Wilkinson, że | ||
* w ogólnym przypadku, zachodzi oszacowanie <math> | * w ogólnym przypadku, zachodzi oszacowanie <math>\rho_N \leq 2^{N-1}</math>, które jest osiągane dla macierzy | ||
<center><math> | <center><math>W = \begin{pmatrix} | ||
1 & & & 1 \\ | 1 & & & 1 \\ | ||
-1 & \ddots & & \vdots\\ | -1 & \ddots & & \vdots\\ | ||
| Linia 327: | Linia 307: | ||
\end{pmatrix} ; | \end{pmatrix} ; | ||
</math></center> | </math></center> | ||
* dla macierzy trójdiagonalnych lub diagonalnie dominujących, lub dla macierzy symetrycznych dodatnio określonych, <math> | * dla macierzy trójdiagonalnych lub diagonalnie dominujących, lub dla macierzy symetrycznych dodatnio określonych, <math>\rho_N \leq 2</math>; | ||
* w średnim przypadku, obserwuje się <math> | * w średnim przypadku, obserwuje się <math>\rho_N \leq N^{2/3}</math>, to znaczy macierze spotykane w praktyce obliczeniowej mają mały wskaźnik wzrostu. | ||
Konkluzja jest więc taka, że <strong>algorytm eliminacji Gaussa z wyborem w kolumnie | Konkluzja jest więc taka, że <strong>algorytm eliminacji Gaussa z wyborem w kolumnie | ||
jest ''praktycznie'' numerycznie poprawny</strong>. Z drugiej strony, dla bardzo dużych | jest ''praktycznie'' numerycznie poprawny</strong>. Z drugiej strony, dla bardzo dużych | ||
<math> | <math>N</math> i niezbyt dobrze uwarunkowanych macierzy, może okazać się, że arytmetyka | ||
pojedynczej precyzji może okazać się niewystarczająca dla uzyskania godnego | pojedynczej precyzji może okazać się niewystarczająca dla uzyskania godnego | ||
wyniku. | wyniku. | ||
Algorytm eliminacji Gaussa z pełnym wyborem elementu głównego jest | Algorytm eliminacji Gaussa z pełnym wyborem elementu głównego jest | ||
numerycznie poprawny, ze wskaźnikiem wzrostu <math> | numerycznie poprawny, ze wskaźnikiem wzrostu <math>\rho_N \leq \sqrt{n\cdot 2 \cdot | ||
3^{1/2}\cdot 4^{1/3}\cdots N^{1/(N-1)}}</math>, a w praktyce grubo poniżej <math> | 3^{1/2}\cdot 4^{1/3}\cdots N^{1/(N-1)}}</math>, a w praktyce grubo poniżej <math>\sqrt{N}</math>. | ||
==Literatura== | ==Literatura== | ||
Aktualna wersja na dzień 21:45, 11 wrz 2023
Uwarunkowanie układu równań liniowych
<<< Powrót do strony głównej przedmiotu Metody numeryczne
Zajmiemy się wrażliwością układu równań na zaburzenia danych: prawej strony i współczynników macierzy układu. Jak zobaczymy na poniższym przykładzie, bywają równania, które są mało podatne na zaburzenia danych (a więc: dobrze uwarunkowane) oraz równania, które są szalenie wrażliwe na zaburzenia, a więc źle uwarunkowane. Jak wkrótce się przekonamy, czułość danego układu równań na zaburzenia da się precyzyjnie scharakteryzować, a cecha ta nie tylko będzie miała wpływ na jakość rozwiązań możliwych do uzyskania w arytmetyce skończonej precyzji, ale także na efektywność metod iteracyjnych rozwiązywania układów równań liniowych, w których są tysięce (lub więcej) niewiadomych.
Przykład: Uwarunkowanie układu dwóch równań liniowych
Rozwiązanie układu dwóch równań liniowych można przedstawić w formie graficznej: jest to punkt przecięcia się dwóch prostych wyznaczonych przez dane współczynniki i wyrazy prawej strony.






A więc równania liniowe mogą, choć nie muszą, być bardzo podatne na zaburzenia danych. Gdy zamiast prawej strony, zaburzymy wyrazy macierzy układu, może nawet okazać się, że dostaniemy układ równań sprzecznych (czy możesz podać przykład?)
Aby przedstawić ogólną teorię zaburzeń dla układów równań liniowych, musimy mieć narzędzia do pomiaru błędu rozwiązań, a także zaburzeń danych zadania: czyli macierzy i wektora prawej strony. Temu będą służyć normy.
Normy wektorowe i macierzowe
Aby badać odległość między rozwiązaniem dokładnym układu równań a jego wartością przybliżoną uzyskaną np. algorytmem eliminacji Gaussa, będziemy posługiwać się normami wektorów i macierzy . Najczęściej używanymi normami wektorowymi będą normy -te,
oraz
W szczególności, norma jest dobrze nam znaną normą euklidesową wektora.
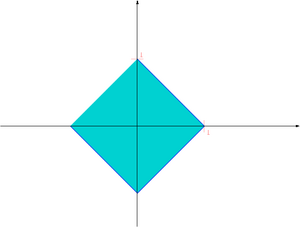
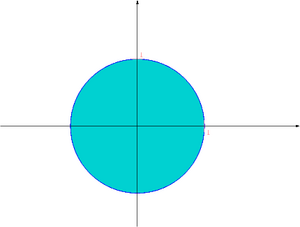
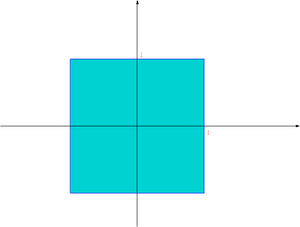
Normą macierzową jest norma Frobeniusa
a także normy indukowane przez normy wektorowe (np. przez normy -te)
Jeśli norma macierzowa jest indukowana przez normę wektorową, to dla dowolnego wektora mamy
Przypomnijmy, że w przestrzeniach liniowych skończenie wymiarowych (a więc także w i w przestrzeni macierzy wymiaru ) każde dwie normy są równoważne. To znaczy, że jeśli mamy dwie normy i w przestrzeni skończenie wymiarowej , to istnieją stałe takie, że
W szczególności dla mamy
a dla mamy
gdzie .
Dla macierzy mamy
oraz
Dowód tego faktu zostawiamy jako ćwiczenie.
Uwarunkowanie układu równań liniowych
Wyprowadzimy teraz wynik świadczący o tym, jak zaburzenie względne danych przenosi się na błąd względny wyniku rozwiązania układu równań liniowych .
Twierdzenie O uwarunkowaniu układu równań
Niech i będą zaburzeniami odpowiednio macierzy i wektora na poziomie względnym , tzn.
Jeśli
to układ zaburzony ma jednoznaczne rozwiązanie spełniające
gdzie definiujemy współczynnik uwarunkowania układu
Zauważmy najpierw, że zachodzi
Lemat Neumanna o otwartości zbioru macierzy odwracalnych
Jeśli jest macierzą taką, że , to macierz jest nieosobliwa oraz
Dowód
Rzeczywiście, gdyby była osobliwa, to istniałby niezerowy wektor taki, że , co implikuje i w konsekwencji . Aby pokazać oszacowanie normy macierzy zauważmy, że
skąd już wynika dowodzona nierówność.
Dowód twierdzenia o uwarunkowaniu
Po podstawieniu mamy teraz
co wobec równości daje, że macierz jest nieosobliwa i układ zaburzony ma jednoznaczne rozwiązanie . Przedstawmy to rozwiązanie w postaci . Rozpisując układ zaburzony i wykorzystując równość otrzymujemy, że , czyli
a stąd
co kończy dowód.
Gdy więc np. , oszacowanie błędu rozwiązania układu zaburzonego możemy zastąpić czytelniejszym (choć mniej precyzyjnym)
Octave i MATLAB mają wbudowane funkcje wyznaczające normy wektorów i macierzy
N = 3; x = [1:N]' A = pascal(N) norm(A,1) norm(x,2) norm(A,Inf)
a także funkcje wyznaczające uwarunkowanie macierzy, przy czym Octave liczy tylko uwarunkowanie w normie :
cond(A)
W LAPACKu służy do tego funkcja DGECON. Zadanie wyznaczania uwarunkowania macierzy jest zadaniem bardzo intensywnym numerycznie. Problem, czy da się je wyznaczyć z dobrą dokładnością kosztem niższym niż wyznaczenie macierzy odwrotnej i jej normy, jest wciąż otwarty.
W praktyce obliczeniowej trafiają się zarówno układy dobrze uwarunkowane, jak i macierze, których uwarunkowanie może być patologicznie duże (np. takie macierze są chlebem powszednim osób rozwiązujących równania różniczkowe).
Przykład: Macierz Hilberta
Przykładem macierzy o uwarunkowaniu wyjątkowo szybko rosnącym z wymiarem jest m.in. macierz Hilberta , gdzie

Taką macierz możemy wygenerować w Octave komendą hilb(N). Jest to bardzo specyficzna macierz, co m.in. przejawia się tym, że uwarunkowanie macierzy Hilberta rośnie eksponencjalnie z , :
Numeryczna poprawność eliminacji Gaussa
Przedstawimy bez dowodu klasyczne twierdzenie o "praktycznej numerycznej poprawności" eliminacji Gaussa z wyborem w kolumnie.
Twierdzenie Wilkinsona
Algorytm eliminacji Gaussa z wyborem elementu głównego w kolumnie, zrealizowany w arytmetyce ,
wyznacza taki, że jest dokładnym rozwiązaniem zadania zaburzonego
przy czym
dla pewnej niedużej stałej . Wskaźnik wzrostu definiujemy tutaj jako
gdzie i są numerycznie wyznaczonymi czynnikami rozkładu PALU.
Jak widzimy, kluczowe dla numerycznej poprawności jest oszacowanie wskaźnika wzrostu . Okazuje się, co wiedział już Wilkinson, że
- w ogólnym przypadku, zachodzi oszacowanie , które jest osiągane dla macierzy
- dla macierzy trójdiagonalnych lub diagonalnie dominujących, lub dla macierzy symetrycznych dodatnio określonych, ;
- w średnim przypadku, obserwuje się , to znaczy macierze spotykane w praktyce obliczeniowej mają mały wskaźnik wzrostu.
Konkluzja jest więc taka, że algorytm eliminacji Gaussa z wyborem w kolumnie jest praktycznie numerycznie poprawny. Z drugiej strony, dla bardzo dużych i niezbyt dobrze uwarunkowanych macierzy, może okazać się, że arytmetyka pojedynczej precyzji może okazać się niewystarczająca dla uzyskania godnego wyniku.
Algorytm eliminacji Gaussa z pełnym wyborem elementu głównego jest numerycznie poprawny, ze wskaźnikiem wzrostu , a w praktyce grubo poniżej .
Literatura
W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj rozdział 4.4 i, nieobowiązkowo, 4.5 w
- D. Kincaid, W. Cheney Analiza numeryczna, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X.
Bardzo dużo informacji na temat omawianych zagadnień znajduje się w monografiach
- A.Kiełbasiński, H. Schwetlick, Numeryczna algebra liniowa, Wydawnictwa Naukowo-Techniczne, Warszawa, 1992,
- N. Higham, Accuracy and Stability of Numerical Algorithms, SIAM, 2002.