MO Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| (Nie pokazano 13 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
| Linia 29: | Linia 29: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Niewątpliwie najwięcej traktatów napisano o Bogu, następnie o miłości, ale jaki temat jest na trzecim miejscu? Patrioci optymalizacji twierdzą, że o optymalizacji (sam w domu mam ponad trzydzieści książek poświeconych tej tematyce). Dlatego (optymalny?) wybór tego co najistotniejsze z tej przywalającej człowieka góry informacji nie jest łatwy. Zatem prezentowane dalej rozważania odzwierciedlają mój punkt widzenia na to co ważne, a co można pominąć z nagromadzonej wiedzy związanej z '''metodami optymalizacji''' i zdaję sobie sprawę z tego, że mój wybór może być krytykowany. | ||
|} | |} | ||
---- | ----- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Optymalizują | ||
*<u>ludzie</u> w życiu codziennym – z reguły staramy się minimalizować nakłady potrzebne do osiągnięcia wybranego celu; | |||
*<u>ludzie</u> w organizacjach – zarząd korporacji podejmuje decyzje, które mają przynieść maksymalny zysk; | |||
*<u>przyroda</u> – łańcuch układa się tak, że jego energia potencjalna jest najmniejsza, promienie światła biegną tak aby minimalizować czas podróży. | |||
|} | |} | ||
---- | ----- | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 83: | Linia 88: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd15.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|We wzorze określającym zysk:<br><math>p^u_j</math> – cena jednostki <math>j</math>-tej benzyny w kontrakcie,<br> | ||
<math>p^v_j</math> – cena jednostki <math>j</math>-tej benzyny w wolnej sprzedaży,<br><math>p^z_i</math> – cena jednostki <math>i</math>-tego komponentu w wolnej sprzedaży,<br><math>c^s_i</math> – koszt wytworzenia jednostki komponentu <math>i</math>,<br><math>c^b_i</math> – koszty komponowania przeliczone na jednostkę komponentu <math>i</math>. | |||
|} | |} | ||
---- | ----- | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 107: | Linia 114: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd19.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd19.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Współczynniki <math>\eta_i</math> i <math>\mu_j</math> można traktować dla benzyn np. jako liczbę oktanową. | ||
|} | |} | ||
---- | ---- | ||
| Linia 143: | Linia 150: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd25.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Automatycy przy projektowaniu układów sterowania zamiast „opisem różniczkowym” obiektu liniowego wolą posługiwać się równoważnym opisem transmitancyjnym przyjmując, że funkcja <math>\varphi(\cdot)</math> będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący <math>\delta(\cdot)</math> mają transformaty Laplace’a. | ||
|} | |} | ||
---- | ---- | ||
| Linia 185: | Linia 192: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd32.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd32.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Zatem do oceny "odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu (32.A), albo całką z kwadratu uchybu (32.B). | ||
|} | |} | ||
---- | ---- | ||
| Linia 281: | Linia 288: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd48.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd48.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przypadku <center><math>x_i^- = -\infty</math> albo <math>x_i^+ = \infty</math>,</center> | ||
nie wykluczamy. | |||
|} | |} | ||
---- | ---- | ||
| Linia 341: | Linia 349: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd58.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd58.png|thumb|500px]] | ||
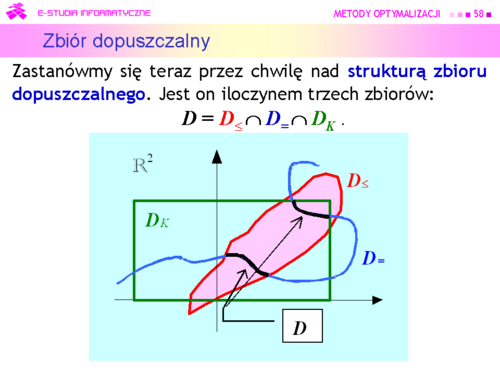
|valign="top"| | |valign="top"|Widać, że najbardziej restrykcyjne są '''ograniczenia równościowe'''. Bez nich przykładowy zbiór dopuszczalny byłby '''spójny''' (składałby się z jednej części) i “miał punkty w środku” (tak jak zbiór z rysunku poprzedniego), matematyk powie: '''miał niepuste wnętrze'''. | ||
|} | |} | ||
---- | ---- | ||
| Linia 461: | Linia 469: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd78.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd78.png|thumb|500px]] | ||
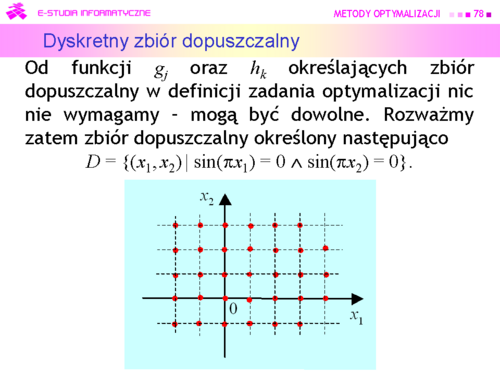
|valign="top"| | |valign="top"|Jest to nieskończony przeliczalny zbiór izolowanych punktów płaszczyzny, a warianty są opisywane wektorami całkowitoliczbowymi. Zbiory tego typu nazywamy '''zbiorami dyskretnymi'''. | ||
Zauważmy, że przedstawiony przykład ograniczeń definiujących zbiór całkowitoliczbowy jest przykładem teoretycznym i ma głównie na celu pokazanie bogactwa "różności” jakie kryje w sobie przyjęta definicja zbioru dopuszczalnego | |||
|} | |} | ||
---- | ---- | ||
| Linia 473: | Linia 483: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd80.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd80.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Niepodzielny produkt to np. lodówka, lub lokówka, ale także paleta z kubeczkami jogurtu. | ||
|} | |} | ||
---- | ---- | ||
| Linia 497: | Linia 507: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd84.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd84.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Jest to funkcja <math>n\cdot m + n +n\cdot m = n(2m + 1)</math> zmiennych. Przy czterech miejscach lokalizacji, <math>n = 4</math>,, i dwudziestu pięciu odbiorcach, <math>m = 25</math>, daje to 204 zmienne. W porównaniu do zadań optymalizacji, które naprawdę są rozwiązywane przy wspomaganiu decyzji podejmowanych przez menedżerów różnych korporacji, gdzie zmiennych potrafi być kilkanaście tysięcy (np. dlatego bo trzeba uwzględnić różne produkty a także różne ich rodzaje), jest to niewiele. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd85.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd85.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Ograniczenia (85.C) mogliśmy zapisać w takiej postaci, bo jeżeli w miejscu <math>i</math> nie zostanie wybudowana nowa fabryka to, <math>y_i = 0</math>, zatem na mocy (85.A) i (85.B), dla każdego <math>j</math> wielkość przewozu <math>x_i_j = 0</math>. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd86.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd86.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Są to związki logiczne a nie nierówności. Nie pasują zatem do przyjętego sposobu określania zbioru dopuszczalnego! | ||
|} | |} | ||
---- | ---- | ||
| Linia 527: | Linia 537: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd89.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd89.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przez <math>\mathbb{Z}</math> oznaczono zbiór liczb całkowitych tj. zbiór<br><math>\{...,-1,0,1,2,...\}</math>. | ||
|} | |} | ||
---- | ---- | ||
| Linia 539: | Linia 549: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd91.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd91.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Mamy zadania optymalizacji (wektory rzeczywiste, jak mówimy zmienne są ciągłe) i zadania dyskretne (wektory całkowitoliczbowe – zmienne dyskretne) mogą więc być '''zadania mieszane''', w których część zmiennych jest ciągła, a pozostała – dyskretna. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M1_Slajd92.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd92.png|thumb|500px]] | ||
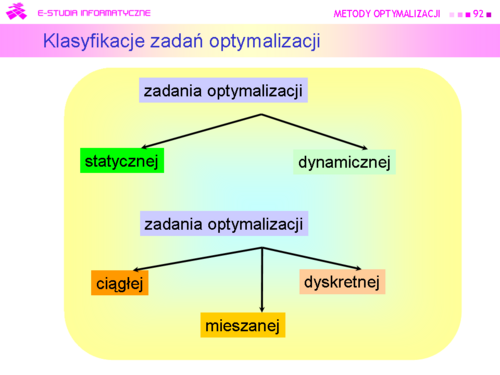
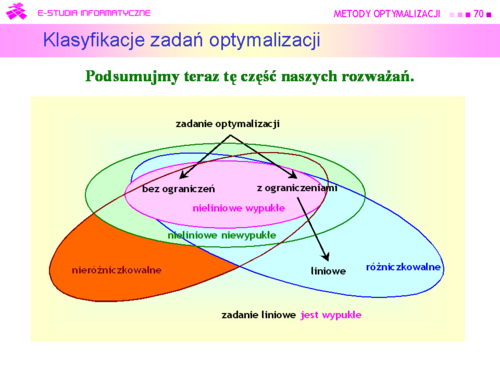
|valign="top"| | |valign="top"|Przedstawione dotąd rozważania pokazały, że analizując zadania optymalizacji, obok zwrócenia uwagi na stopień trudności znajdowania ich rozwiązania („łatwiejsze – trudniejsze”, czyli: bez ograniczeń – z ograniczeniami, liniowe – nieliniowe itp.) trzeba także zwrócić uwagę na ich strukturę, co prowadzi do klasyfikacji takiej jak na rysunku. | ||
|} | |} | ||
---- | ---- | ||
Aktualna wersja na dzień 10:28, 5 wrz 2023
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
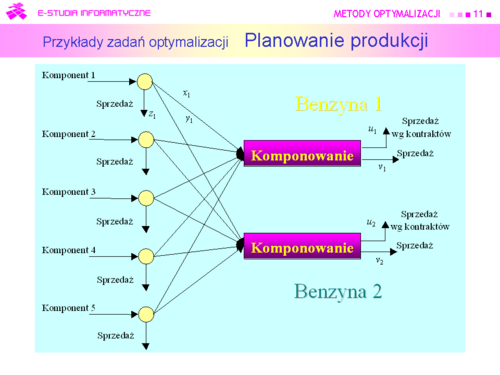
Współczynniki i można traktować dla benzyn np. jako liczbę oktanową. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
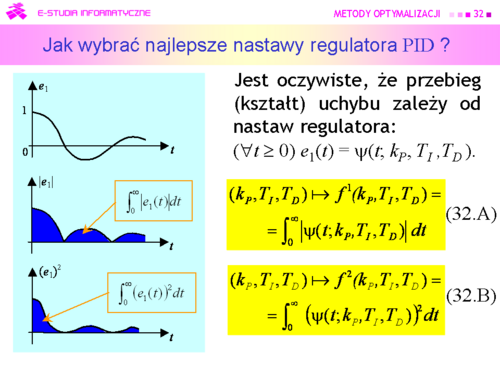 |
Zatem do oceny "odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu (32.A), albo całką z kwadratu uchybu (32.B). |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Przypadku nie wykluczamy. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Niepodzielny produkt to np. lodówka, lub lokówka, ale także paleta z kubeczkami jogurtu. |
 |
 |
 |
 |
Ograniczenia (85.C) mogliśmy zapisać w takiej postaci, bo jeżeli w miejscu nie zostanie wybudowana nowa fabryka to, , zatem na mocy (85.A) i (85.B), dla każdego wielkość przewozu . |
 |
Są to związki logiczne a nie nierówności. Nie pasują zatem do przyjętego sposobu określania zbioru dopuszczalnego! |
 |
 |
 |
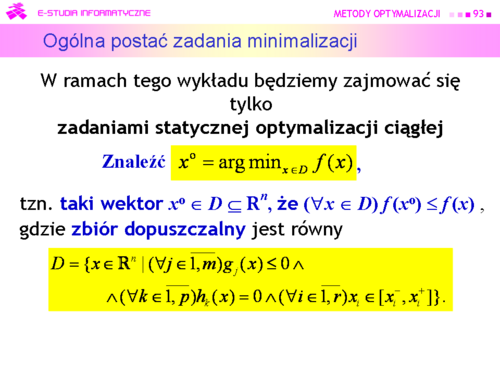
Przez oznaczono zbiór liczb całkowitych tj. zbiór . |
 |
 |