SO-1st-2.3-w11.tresc-1.0-Slajd28: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 6: | Linia 6: | ||
Rozwiązanie to jest wynikiem połączenia podejścia 1 i 2. Za pośrednictwem tablicy ''znacznik'' procesy informują się nawzajem o swoim stanie, a za pośrednictwem zmiennej ''numer'' rozstrzygają ewentualny konflikt. Jeśli zatem wartość w tablicy ''znacznik'' na pozycji odpowiadającej procesowi rywalizującemu jest ustawiona na false, to nie ubiega się on o sekcję krytyczną. Następuje wówczas opuszczenie pętli '''while''' , tym samym sekcji wejściowej i wejście do sekcji krytycznej. W przypadku, gdy dwa rywalizujące procesu ustawią wartość true na swoich pozycjach w tablicy ''znacznik'' , rozstrzygnięcie sporu zależy od wartości zmiennej ''numer'' . Ten z procesów, który później ustawi w niej numer rywala, ten musi poczekać, aż rywal wyjdzie z sekcji krytycznej. | Rozwiązanie to jest wynikiem połączenia podejścia 1 i 2. Za pośrednictwem tablicy ''znacznik'' procesy informują się nawzajem o swoim stanie, a za pośrednictwem zmiennej ''numer'' rozstrzygają ewentualny konflikt. Jeśli zatem wartość w tablicy ''znacznik'' na pozycji odpowiadającej procesowi rywalizującemu jest ustawiona na false, to nie ubiega się on o sekcję krytyczną. Następuje wówczas opuszczenie pętli '''while''' , tym samym sekcji wejściowej i wejście do sekcji krytycznej. W przypadku, gdy dwa rywalizujące procesu ustawią wartość true na swoich pozycjach w tablicy ''znacznik'' , rozstrzygnięcie sporu zależy od wartości zmiennej ''numer'' . Ten z procesów, który później ustawi w niej numer rywala, ten musi poczekać, aż rywal wyjdzie z sekcji krytycznej. | ||
Przedstawione rozwiązanie znane jest pod nazwą ''algorytmu'' ''Petersona'' . Algorytm ten można uogólnić na ''n'' procesów, stosując podejście „wieloetapowe”. Na każdym etapie eliminowany jest jeden proces. Zmienna ''numer'' musi być wówczas tablicą '' | Przedstawione rozwiązanie znane jest pod nazwą ''algorytmu'' ''Petersona'' . Algorytm ten można uogólnić na ''n'' procesów, stosując podejście „wieloetapowe”. Na każdym etapie eliminowany jest jeden proces. Zmienna ''numer'' musi być wówczas tablicą ''n''-1 - elementową, a tablica ''znacznik'' przechowuje numer etapu, na którym jest dany proces. | ||
[[SO-1st-2.3-w11.tresc-1.0-Slajd27 | << Poprzedni slajd]] | [[SO-1st-2.3-w11.tresc-1.0-toc|Spis treści ]] | [[SO-1st-2.3-w11.tresc-1.0-Slajd29 | Następny slajd >>]] | [[SO-1st-2.3-w11.tresc-1.0-Slajd27 | << Poprzedni slajd]] | [[SO-1st-2.3-w11.tresc-1.0-toc|Spis treści ]] | [[SO-1st-2.3-w11.tresc-1.0-Slajd29 | Następny slajd >>]] | ||
Aktualna wersja na dzień 13:43, 22 wrz 2006
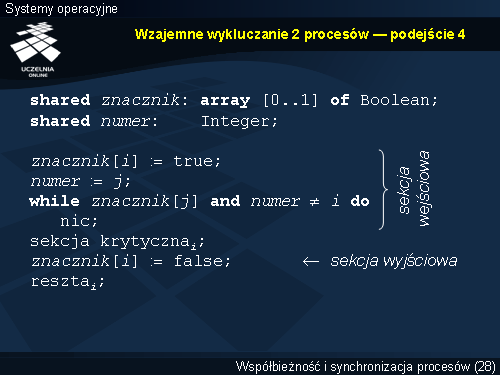
Wzajemne wykluczanie 2 procesów — podejście 4
Rozwiązanie to jest wynikiem połączenia podejścia 1 i 2. Za pośrednictwem tablicy znacznik procesy informują się nawzajem o swoim stanie, a za pośrednictwem zmiennej numer rozstrzygają ewentualny konflikt. Jeśli zatem wartość w tablicy znacznik na pozycji odpowiadającej procesowi rywalizującemu jest ustawiona na false, to nie ubiega się on o sekcję krytyczną. Następuje wówczas opuszczenie pętli while , tym samym sekcji wejściowej i wejście do sekcji krytycznej. W przypadku, gdy dwa rywalizujące procesu ustawią wartość true na swoich pozycjach w tablicy znacznik , rozstrzygnięcie sporu zależy od wartości zmiennej numer . Ten z procesów, który później ustawi w niej numer rywala, ten musi poczekać, aż rywal wyjdzie z sekcji krytycznej.
Przedstawione rozwiązanie znane jest pod nazwą algorytmu Petersona . Algorytm ten można uogólnić na n procesów, stosując podejście „wieloetapowe”. Na każdym etapie eliminowany jest jeden proces. Zmienna numer musi być wówczas tablicą n-1 - elementową, a tablica znacznik przechowuje numer etapu, na którym jest dany proces.