Programowanie funkcyjne/Podstawy: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „ </math>” na „</math>” |
|||
| (Nie pokazano 22 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
== Wstęp == | == Wstęp == | ||
<p align="justify"> W '''każdym''' języku programowania mamy trzy rodzaje konstrukcji | <p align="justify"> | ||
językowych: | W '''każdym''' języku programowania mamy trzy rodzaje konstrukcji językowych: | ||
* | |||
* | * Podstawowe symbole -- Są to te byty występujące w języku (typy, wartości, operacje, relacje, procedury itp.), które są wbudowane w język i nie trzeba ich definiować. | ||
* | |||
< | * Sposoby konstrukcji -- Są to wszystkie te konstrukcje językowe, które pozwalają budować z prostszych elementów języka bardziej skomplikowane całości. | ||
* typy | * Sposoby abstrakcji -- Są to te konstrukcje językowe, które pozwalają złożonym konstrukcjom nadawać nazwy. Nazwane konstrukcje mogą być dalej wykorzystywane tak, jak podstawowe symbole języka. | ||
* | </p> | ||
* | |||
<p align="justify"> | |||
W językach imperatywnych, takich jak Pascal, C czy C++ przykładami symboli podstawowych są: | |||
* typy proste, takie jak <tt>integer</tt> i <tt>float</tt>, | |||
* stałe takie jak <tt>0</tt>, <tt>1</tt>, <tt>2.3</tt>, | |||
* operacje arytmetyczne, procedury implementowane przez biblioteki standardowe lub wbudowane (udostępniane przez bibliotekę ''run-time library''). | |||
Przykładami sposobów konstrukcji są: | |||
* wyrażenia, | |||
* typy złożone, takie jak tablice, struktury (rekordy) czy wskaźniki, | |||
* instrukcje złożone, takie jak instrukcja warunkowa, pętle czy bloki instrukcji. | |||
Do sposobów abstrakcji zaliczamy wszelkiego rodzaju definicje: definicje stałych, typów czy procedur. | |||
Niektóre konstrukcje językowe mogą łączyć ze sobą sposoby konstrukcji i abstrakcji. | |||
Najczęściej sposoby definicji zawierają w sobie sposoby konstrukcji. | |||
Na przykład, definicja procedury zwykle zawiera (jako ciało definiowanej procedury) blok instrukcji. | |||
Podobnie, niektóre sposoby konstrukcji wymagają, aby konstruowane całości były nazwane. | |||
Na przykład, w Pascalu typy argumentów procedur muszą być nazwane. | |||
</p> | |||
<p align="justify"> | |||
Czytelnikowi może w tej chwili wydawać się, że rozróżnianie sposobów konstrukcji i abstrakcji to dzielenie włosa na czworo. | |||
Jak zobaczymy w trakcie tego kursu, odróżnienie jednego od drugiego prowadzi do pewnych specyficznych konstrukcji językowych. | |||
</p> | </p> | ||
== BNF == | == BNF == | ||
<p align="justify"> | <p align="justify"> | ||
W kolejnych wykładach będziemy przedstawiać rozmaite konstrukcje językowe Ocamla. | |||
Do opisu składni tych konstrukcji, oprócz języka nieformalnego i przykładów, | |||
będziemy używać notacji [http://en.wikipedia.org/wiki/Backus%E2%80%93Naur_form BNF] | |||
(rozszerzenie gramatyk bezkontekstowych | (ang. ''Backus–Naur form''). | ||
Jest to rozszerzenie gramatyk bezkontekstowych, poręczne przy opisywaniu składni języków programowania. | |||
Notacja ta ma następującą postać: | |||
*< | * W BNF-ie definiujemy możliwe postaci rozmaitych ''konstrukcji składniowych''. Konstrukcje te mają nazwy postaci: <tt><konstrukcja></tt>. Odpowiadają one nieterminalom w gramatykach bezkontekstowych. | ||
*< | * Opis składni składa się z szeregu reguł postaci <tt><konstrukcja> ::= możliwa postać</tt>. Reguły te opisują możliwe postaci poszczególnych konstrukcji składniowych. Jeżeli dla danej konstrukcji mamy wiele reguł, to traktujemy je jak alternatywy. Reguły te odpowiadają produkcjom w gramatykach bezkontekstowych. | ||
*< | * Po prawej stronie reguł możemy używać następujących konstrukcji: | ||
*< | ** podając tekst, który ma się pojawić dosłownie, będziemy go podkreślać, na przykład: <tt><u>słowo_kluczowe</u></tt>, | ||
*< | ** nazw konstrukcji składniowych możemy używać również po prawej stronie reguł, na oznaczenie miejsc, w których się one pojawiają, | ||
*< | ** chcąc opisać alternatywne postaci danej konstrukcji używamy pionowej kreski, <tt>...|...</tt>, | ||
*< | ** tekst umieszczony w kwadratowych nawiasach jest opcjonalny <tt>[...]</tt>, | ||
** dodatkowo, możemy używać nawiasów (wąsatych): <tt> {...}</tt>, | |||
< | ** tekst umieszczony w nawiasach postaci <tt>{...}<sup>*</sup></tt> może się powtarzać zero, jeden lub więcej razy, | ||
** tekst umieszczony w nawiasach postaci <tt>{...}<sup>+</sup></tt> może się powtarzać jeden lub więcej razy. | |||
</p> | |||
{{przyklad|[Adresy pocztowe]||}} | |||
BNF może byc użyty do opisywania składni najrozmaitszych rzeczy. | |||
Oto opis składni adresów pocztowych: | |||
<tt> | |||
<adres> ::= <adresat> <adres lokalu> <adres miasta> <adres kraju> | |||
<adresat> ::= [<u>W.P.</u> | <u>Sz.Pan.</u>] <napis> <u>,</u> | |||
<adres lokalu> ::= <ulica> <numer> [ <u>/</u> <numer> ] [<u>m</u> <numer> |<u>/</u> <numer> ] <u>,</u> | |||
<adres miasta> ::= [<kod>] <napis> | |||
<adres kraju> ::= [<u>,</u> <napis>] | |||
<kod> ::= <cyfra> <cyfra> <u>-</u> <cyfra> <cyfra> <cyfra> | |||
<cyfra> ::= <u>0</u> | <u>1</u> | <u>2</u> | <u>3</u> | <u>4</u> | <u>5</u> | <u>6</u> | <u>7</u> | <u>8</u> | <u>9</u> | |||
<numer> ::= <cyfra> [<numer>] | |||
</tt> | |||
Specyfikacja ta oczywiście nie jest kompletna, gdyż nie definiuje czym jest napis. | |||
<p align="justify"> | |||
Pamiętajmy, że czym innym jest symbol, a czym innym jego znaczenie (semantyka). | |||
BNF służy jedynie do opisu składni. | |||
</p> | </p> | ||
| Linia 37: | Linia 77: | ||
<p align="justify"> | <p align="justify"> | ||
Kompilator Ocamla działa w sposób inkrementacyjny, tzn. | Kompilator Ocamla działa w sposób przyrostowy (inkrementacyjny), tzn. | ||
działa w cyklu powtarzając następujące czynności: | działa w cyklu powtarzając następujące czynności: | ||
*wczytuje fragment programu, | * wczytuje fragment programu, | ||
*kompiluje go, dołączając do już skompilowanych fragmentów, | * kompiluje go, dołączając do już skompilowanych fragmentów, | ||
*wykonuje wprowadzony fragment. | * wykonuje wprowadzony fragment. | ||
Nazwa "tryb przyrostowy" bierze się stąd, że kompilator nie musi generować całego kodu od razu, lecz kod ten przyrasta z każdym cyklem. | |||
<br/> | <br/> | ||
Taki fragment programu będziemy nazywać ''jednostką kompilacji''. Wykonanie jednostki kompilacji może zarówno powodować | Taki fragment programu, wprowadzany i kompilowany w jednym cyklu, będziemy nazywać ''jednostką kompilacji''. | ||
Wykonanie jednostki kompilacji może zarówno powodować obliczenie wartości, jak i definiowanie nowych pojęć. | |||
Każda jednostka kompilacji musi być w Ocamlu | Każda jednostka kompilacji musi być w Ocamlu zakończona przez <tt>;;</tt>. | ||
zakończona przez <tt>;;</tt> | |||
</p> | </p> | ||
<program> ::= { <jednostka kompilacji> <u>;;</u> }* | <program> ::= { <jednostka kompilacji> <u>;;</u> }<sup>*</sup> | ||
== Podstawowe symbole Ocamla == | |||
<p align="justify"> | |||
Podstawowe symbole Ocamla obejmują m.inn: | |||
* typy: | |||
** <tt>bool</tt> -- wartości logiczne, | |||
** <tt>int</tt> -- liczby całkowite, | |||
** <tt>float</tt> -- liczby zmiennopozycyjne, | |||
** <tt>char</tt> -- znaki, | |||
** <tt>string</tt> -- napisy, | |||
* stałe: | |||
** logiczne (<tt>true</tt> i <tt>false</tt>), | |||
** całkowite (np.: <tt>0</tt>, <tt>1</tt>, <tt>-2</tt>), | |||
** zmiennopozycyjne (np.: <tt>2.3</tt>, <tt>-3.4</tt>, <tt>4.5e-7</tt>), | |||
** znakowe (np.: <tt>'a'</tt>), | |||
** napisy (np. <tt>"ala ma kota"</tt>). | |||
* procedury: | |||
** operacje arytmetyczne na liczbach całkowitych: <tt>+</tt>, <tt>-</tt>, <tt>*</tt>, <tt>/</tt>, <tt>mod</tt>, | |||
** operacje arytmetyczne na liczbach zmiennopozycyjnych (zapisujemy je tak samo jak analogiczne operacje na liczbach całkowitych, ale dodając kropkę): <tt>+.</tt>, <tt>-.</tt>, <tt>*.</tt>, <tt>/.</tt>, | |||
** operacje logiczne: | |||
*** <tt>||</tt> (alternatywa), | |||
*** <tt>&&</tt> (koniunkcja), | |||
*** <tt>not</tt> (negacja), | |||
** sklejanie (konkatenacja) napisów <tt>^</tt>, | |||
** relacje (określone dla wszystkich typów): <tt> =</tt>, <tt><=</tt>, <tt>>=</tt>, <tt><</tt>, <tt>></tt>, <tt><></tt>. | |||
</p> | |||
== Wyrażenia == | == Wyrażenia == | ||
<p align="justify"> | <p align="justify"> | ||
Najprostsza jednostka kompilacji i podstawowa konstrukcja | Najprostsza jednostka kompilacji i podstawowa konstrukcja programistyczna to wyrażenia. | ||
programistyczna | Wyrażenia budujemy w standardowy sposób za pomocą stałych, procedur i nawiasów. | ||
Wyrażenia budujemy w standardowy sposób za pomocą stałych, | (Operacje arytmetyczne traktujemy tak jak inne procedury, z dokładnością do tego, że zapisujemy je infiksowo). | ||
procedur i nawiasów. | Jedynym odstępstwem jest to, że argumenty procedur nie muszą być objęte nawiasami i pooddzielane przecinkami. | ||
Jedynym odstępstwem jest to, że argumenty procedur nie muszą | Operacje, które standardowo zapisujemy infiksowo (np. operacje arytmetyczne) mają również postać infiksową. | ||
być objęte nawiasami i pooddzielane przecinkami. | Rozróżniamy operacje arytmetyczne na liczbach całkowitych i rzeczywistych -- te ostatnie mają dodaną kropkę. | ||
Operacje, które standardowo zapisujemy infiksowo (np. operacje | |||
arytmetyczne) mają również postać infiksową. | |||
Rozróżniamy operacje arytmetyczne na liczbach całkowitych i | |||
rzeczywistych - te ostatnie mają dodaną kropkę. | |||
</p> | </p> | ||
{{przyklad|[Wyrażenia]||}} | |||
''- : int = | 42;; | ||
''- : int = 42'' | |||
''- : int = | |||
36 + 6;; | |||
''- : int = | ''- : int = 42'' | ||
''- : int = | 3 * 14;; | ||
1*2*3*4*5 | ''- : int = 42'' | ||
''- : int = | |||
100 - 58;; | |||
''- : float = | ''- : int = 42'' | ||
1 * 2 * 3 * 4 * 5 - ((6 + 7) * 8 * 9 / 12);; | |||
''- : int = 42'' | |||
silnia 7 / silnia 5;; | |||
''- : int = 42'' | |||
596.4 /. 14.2;; | |||
''- : float = 42.'' | |||
"ala" ^ " ma " ^ "kota";; | "ala" ^ " ma " ^ "kota";; | ||
''- : string = "ala ma kota"'' | ''- : string = "ala ma kota"'' | ||
| Linia 84: | Linia 154: | ||
<p align="justify"> | <p align="justify"> | ||
Wszystko, czego potrzeba do budowy wyrażeń, to: | Wszystko, czego potrzeba do budowy wyrażeń, to: | ||
*stałe (liczbowe, napisy, lub nazwy stałych), | * stałe (liczbowe, napisy, lub nazwy stałych), | ||
*zastosowanie | * zastosowanie procedur do argumentów, | ||
* | * nawiasy. | ||
<br/> | <br/> | ||
Zauważmy, że procedury i ich argumenty są tu traktowane na równi - | Zauważmy, że procedury i ich argumenty są tu traktowane na równi - | ||
| Linia 97: | Linia 167: | ||
<jednostka kompilacji> ::= <wyrażenie> | ... | <jednostka kompilacji> ::= <wyrażenie> | ... | ||
<wyrażenie> ::= <u>(</u> <wyrażenie> <u>)</u> | { <wyrażenie> }+ | | <wyrażenie> ::= <u>(</u> <wyrażenie> <u>)</u> | { <wyrażenie> }<sup>+</sup> | <operator unarny> <wyrażenie> | | ||
<wyrażenie> <operator binarny> <wyrażenie> | <identyfikator> | | |||
<wyrażenie> <operator binarny> <wyrażenie> | | <stała całkowita> | <stała zmiennopozycyjna> | <stała napisowa> | ... | ||
<operator unarny > ::= <u>-</u> | <u>not</u> | ... | <operator unarny > ::= <u>-</u> | <u>not</u> | ... | ||
<operator binarny> ::= <u>+</u> | <u>+.</u> | <u>-</u> | <u>-.</u> | <u>*</u> | <u>*.</u> | <u>/</u> | <u>/.</u> | | <operator binarny> ::= <u>+</u> | <u>+.</u> | <u>-</u> | <u>-.</u> | <u>*</u> | <u>*.</u> | <u>/</u> | <u>/.</u> | | ||
<u>mod</u> | <u>||</u> | <u>&&</u> | <u>=</u> | <u><</u> | <u><=</u> | <u>></u> | <u>>=</u> | <u>^</u> | ... | <u>mod</u> | <u>||</u> | <u>&&</u> | <u>=</u> | <u><</u> | <u><=</u> | <u>></u> | <u>>=</u> | <u>^</u> | ... | ||
{{uwaga||uwaga_3| | |||
Powyższy opis składni nie jest jednoznaczny, tzn. ten sam program może zostać rozłożony składniowo na więcej niż jeden sposób (ale dzięki temu jest bardziej czytelny). | |||
Nie będziemy aż tak formalni. | |||
Zamiast tego ewentualne niejednoznaczności będziemy wyjaśniać w sposób opisowy. | |||
}} | |||
<p align="justify"> | <p align="justify"> | ||
Zastosowania procedur wiążą najsilniej, operatory unarne słabiej, | Zastosowania procedur wiążą najsilniej, operatory unarne słabiej, | ||
a operatory binarne najsłabiej, przy czym zachowana jest tradycyjna | a operatory binarne najsłabiej, przy czym zachowana jest tradycyjna | ||
kolejność wiązania operacji arytmetycznych. | kolejność wiązania operacji arytmetycznych. | ||
</p> | </p> | ||
===Obliczanie wartości wyrażeń=== | ===Obliczanie wartości wyrażeń=== | ||
<p align="justify"> | <p align="justify"> | ||
Efektem "działania" wyrażenia jest jego wartość. | Efektem "działania" wyrażenia jest jego wartość. | ||
Rozkład składniowy danego wyrażenia możemy sobie przedstawić w postaci drzewa (tzw. drzewo wyprowadzenia). | |||
W liściach drzewa mamy stałe, a węzły wewnętrzne to procedury. | |||
Nawiasy wraz z priorytetami operatorów wyznaczają kształt takiego drzewa. | |||
</p> | </p> | ||
{{przyklad|[Drzewo wyprowadzenia]||}} | |||
Oto drzewo wyprowadzenia dla wyrażenia <tt>silnia 3 * 7</tt>: | |||
[[Image:Pf-rys-2-1.png|Drzewo wyprowadzenia]] | |||
<p align="justify"> | |||
Wszystkie nazwane stałe są przechowywane w tzw. ''środowisku''. | |||
Przyporządkowuje ono nazwom ich wartości. | |||
Jeśli w wyrażeniu występują nazwy stałych, to ich wartości są pobierane ze środowiska. | |||
Wyliczenie wartości wyrażenia możemy sobie wyobrazić jako udekorowanie drzewa wyprowadzenia wartościami, w kolejności od liści do korzenia. | |||
Wartość w korzeniu to wynik. | |||
</p> | |||
{{przyklad|[Obliczanie wyrażenia]||}} | |||
Oto powyższe drzewo wyprowadzenia udekorowane wartościami: | |||
[[Image:Pf-rys-2-2.png|Udekorowane drzewo wyprowadzenia]] | |||
==Definicje stałych== | ==Definicje stałych== | ||
| Linia 130: | Linia 218: | ||
<definicja> ::= <u>let</u> <identyfikator> <u>=</u> <wyrażenie> | ... | <definicja> ::= <u>let</u> <identyfikator> <u>=</u> <wyrażenie> | ... | ||
<p align="justify"> | |||
Definicji stałej nie da się wyrazić jako procedury ani wyrażenia, ponieważ zmienia ona środowisko. | |||
Dlatego też <tt>let</tt> jest nazywane ''formą specjalną''. | Dlatego też <tt>let</tt> jest nazywane ''formą specjalną''. | ||
"Obliczenie" definicji wykonywane jest następująco: | "Obliczenie" definicji wykonywane jest następująco: | ||
* | * obliczana jest wartość wyrażenia tworzącego definicję, | ||
* | * do środowiska wstawiany jest identyfikator, któremu przyporządkowywana jest wartość obliczonego wyrażenia. | ||
<br/> | <br/> | ||
Jeżeli symbol jest już w środowisku, to można ''przysłonić'' | Jeżeli symbol jest już w środowisku, to można ''przysłonić'' | ||
go i nadać symbolowi nowe znaczenie. | go i nadać symbolowi nowe znaczenie. | ||
</p> | |||
{{ | {{uwaga||uwaga_4|To jest uproszczony model. | ||
uwaga||uwaga_4|To jest uproszczony model, | W miarę jak będziemy poznawać kolejne konstrukcje językowe, będziemy go w miarę potrzeb rozszerzać. | ||
}} | }} | ||
{{przyklad|[ | {{przyklad|[Definicje]||}} | ||
'''let''' a = 4;; | '''let''' a = 4;; | ||
''val a : int = 4'' | |||
'''let''' b = 5 * a;; | '''let''' b = 5 * a;; | ||
''val b : int = 20'' | |||
'''let''' pi = 3.14;; | '''let''' pi = 3.14;; | ||
''val pi : float = 3.14'' | |||
pi *. 4.0 *. 4.0;; | pi *. 4.0 *. 4.0;; | ||
''val - : float = 50.24'' | |||
'''let''' a = "ala";; | '''let''' a = "ala";; | ||
''val a : string = "ala"'' | |||
<p align="justify"> | |||
Możliwe jest też równoczesne definiowanie wielu stałych. | Możliwe jest też równoczesne definiowanie wielu stałych. | ||
W takim przypadku najpierw obliczane są wszystkie wyrażenia, a następnie ich wartości są przypisywane w środowisku odpowiednim identyfikatorom. | |||
</p> | |||
<definicja> ::= <u>let</u> <identyfikator> <u>=</u> <wyrażenie> | <definicja> ::= <u>let</u> <identyfikator> <u>=</u> <wyrażenie> | ||
{ <u>and</u> <identyfikator> <u>=</u> <wyrażenie> }^* | { <u>and</u> <identyfikator> <u>=</u> <wyrażenie> }^* | ||
{{przyklad|[ | {{przyklad|[Definicje równoczesne]||}} | ||
'''let''' a = 4 '''and''' b = 5;; | '''let''' a = 4 '''and''' b = 5;; | ||
''val a : int = 4'' | |||
''val b : int = 5'' | |||
'''let''' a = a + b '''and''' b = a * b;; | '''let''' a = a + b '''and''' b = a * b;; | ||
''val a : int = 9'' | |||
''val b : int = 20'' | |||
==Definicje procedur== | ==Definicje procedur== | ||
<p align="justify"> | |||
Mamy tylko trzy podstawowe konstrukcje językowe: | Mamy tylko trzy podstawowe konstrukcje językowe: | ||
* użycie wartości zdefiniowanej w środowisku (nie ważne liczby | * użycie wartości zdefiniowanej w środowisku (nie ważne liczby czy procedury), | ||
* zastosowanie funkcji do argumentów (np. obliczenie mnożenia), | * zastosowanie funkcji do argumentów (np. obliczenie mnożenia), | ||
* definiowanie nowych wartości. | * definiowanie nowych wartości. | ||
<br/> | <br/> | ||
Jak wcześniej wspomnieliśmy, procedury są równie dobrymi wartościami, | Jak wcześniej wspomnieliśmy, procedury są obywatelami pierwszej kategorii, | ||
jak wszystkie inne. Wynika stąd, że: | czyli równie dobrymi wartościami, jak wszystkie inne. | ||
* można definiować nazwane procedury, | Wynika stąd, że: | ||
* można definiować nazwane procedury (stałe proceduralne), | |||
* procedura może być wartością wyrażenia, | * procedura może być wartością wyrażenia, | ||
* procedury mogą być argumentami i wynikami procedur ( | * procedury mogą być argumentami i wynikami procedur (sic!). | ||
<br/> | <br/> | ||
Definicje nazwanych procedur mają następującą postać: | Definicje nazwanych procedur mają następującą postać: | ||
</p> | |||
<definicja> ::= <u>let</u> <identyfikator> <identyfikator> + <u>=</u> <wyrażenie> | <definicja> ::= <u>let</u> <identyfikator> {<identyfikator>}<sup>+</sup> <u>=</u> <wyrażenie> | ||
Pierwszy z identyfikatorów to nazwa definiowanej procedury, a reszta | <p align="justify"> | ||
< | Pierwszy z identyfikatorów to nazwa definiowanej procedury, a reszta to jej ''parametry formalne''. | ||
Wyrażenie zaś to ''treść'' procedury. | |||
Określa ono wartość procedury, w zależności od wartości argumentów. | |||
Zwróćmy uwagę, że argumenty nie są otoczone nawiasami ani oddzielone przecinkami. | |||
</p> | |||
{{przyklad|[Definicje nazwanych procedur]||}} | {{przyklad|[Definicje nazwanych procedur]||}} | ||
'''let''' square x = x *. x;; | '''let''' square x = x *. x;; | ||
''val square : float -> float = <fun>'' | |||
'''let''' pow r = pi *. (square r);; | '''let''' pow r = pi *. (square r);; | ||
''val pow : float -> float = <fun>'' | |||
pow 4.0;; | pow 4.0;; | ||
''- : float = 50.24'' | ''- : float = 50.24'' | ||
'''let''' twice x = 2 * x;; | '''let''' twice x = 2 * x;; | ||
''val twice : int -> int = <fun>'' | |||
twice (twice 3);; | twice (twice 3);; | ||
''- : int = 12'' | ''- : int = 12'' | ||
'''let''' mocium s = "mocium panie, " ^ s;; | '''let''' mocium s = "mocium panie, " ^ s;; | ||
''val mocium : string -> string = <fun>'' | |||
mocium (mocium "me wezwanie");; | mocium (mocium "me wezwanie");; | ||
- : string = "mocium panie, mocium panie, me wezwanie" | ''- : string = "mocium panie, mocium panie, me wezwanie"'' | ||
<p align="justify"> | |||
Tak jak w przypadku innych wartości, gdy definiujemy procedurę kompilator odpowiada podając nam "typ" tej procedury. | |||
Typ ten zawiera typ argumentu i wyniku połączone strzałką. | |||
Na przykład, <tt>int -> int</tt> oznacza, że argument i wynik procedury są liczbami całkowitymi. | |||
W przypadku większej liczby argumentów zobaczymy większą liczbę strzałek. | |||
Typami procedur zajmiemy się dokładniej, gdy będziemy mówić o procedurach wyższych rzędów. | |||
</p> | |||
'''let''' plus x y = x + y;; | |||
''val plus : int -> int -> int = <fun>'' | |||
<p align="justify"> | |||
W momencie, gdy zastosujemy procedurę do jej argumentów, jej wartość jest obliczana w następujący sposób: | |||
* obliczana jest procedura, którą należy zastosować i jej argumenty, | |||
* na podstawie środowiska (w którym była definiowana procedura) tworzone jest tymczasowe środowisko, w którym dodatkowo parametrom formalnym są przyporządkowane wartości argumentów, | |||
* w tym tymczasowym środowisku obliczane jest wyrażenie stanowiące treść procedury, | |||
* wartość tak obliczonego wyrażenia jest wartością zastosowania procedury do argumentów. | |||
</p> | |||
{{uwaga||uwaga_5|Procedury nie są funkcjami matematycznymi -- | |||
mogą być nieokreślone, np. na skutek dzielenia przez 0, lub ich obliczanie może się zapętlać.}} | |||
Możemy też tworzyć procedury bez nazwy - <math>\lambda</math>-abstrakcja. | === <math>\lambda</math>-abstrakcja === | ||
<p align="justify"> | |||
Możemy też tworzyć procedury bez nazwy, tzn. takie procedury, | |||
które są wartością pewnego rodzaju wyrażeń, | |||
natomiast nie muszą pojawiać się w środowisku. | |||
Procedury takie możemy tworzyć za pomocą tzw. <math>\lambda</math>-abstrakcji. | |||
</p> | |||
<p align="justify"> | |||
Zauważmy, że funkcja, jako pojęcie matematyczne, nie musi mieć nazwy. | |||
Zwykle nadajemy funkcjom nazwy, gdyż tak jest poręcznie. | |||
Na przykład <math>x \mapsto x+1</math> jest również dobrym opisem funkcji | |||
(której wartość jest o 1 większa od argumentu). | |||
<math>\lambda</math>-abstrakcja ma podobną postać. | |||
Składa się ona ze słowa kluczowego <tt>function</tt>, parametru formalnego funkcji, | |||
oraz wyrażenia określającego jej wartość. | |||
</p> | |||
<wyrażenie> ::= <u>function</u> <identyfikator> <u>-></u> <wyrażenie> | <wyrażenie> ::= <u>function</u> <identyfikator> <u>-></u> <wyrażenie> | ||
Wartością takiego wyrażenia jest jednoargumentowa procedura bez nazwy. | <p align="justify"> | ||
< | Wartością takiego wyrażenia jest jednoargumentowa procedura bez nazwy. | ||
Narazie możemy przyjąć, że forma specjalna <tt>let</tt> definiująca procedurę z parametrami | |||
jest lukrem syntaktycznym pokrywającym wyrażenie <tt>function</tt> i definicję stałej. | |||
</p> | |||
<p align="justify"> | |||
Dostępna jest też skrócona forma zapisu nienazwanych procedur wieloargumentowych. | |||
</p> | |||
<wyrażenie> ::= <u>fun</u> {<identyfikator>}<sup>+</sup> <u>-></u> <wyrażenie> | |||
Wyrażenie postaci: | |||
fun x y z -> ... | |||
jest równoważne: | |||
function x -> function y -> function z -> ... | |||
<p align="justify"> | |||
Oto alternatywna definicja procedur z poprzedniego przykładu. | |||
</p> | |||
{{przyklad|[Alternatywne definicje procedur]||}} | {{przyklad|[Alternatywne definicje procedur]||}} | ||
('''function''' x -> x * (x + 1)) (2 * 3);; | |||
''- : int = 42'' | |||
'''let''' square = '''function''' x -> x *. x;; | '''let''' square = '''function''' x -> x *. x;; | ||
''val square : float -> float = <fun>'' | |||
'''let''' pow = '''function''' r -> pi *. (square r);; | '''let''' pow = '''function''' r -> pi *. (square r);; | ||
''val pow : float -> float = <fun>'' | |||
'''let''' twice = '''function''' x -> 2 * x;; | '''let''' twice = '''function''' x -> 2 * x;; | ||
''val twice : int -> int = <fun>'' | |||
'''let''' foo = '''function''' x -> '''function''' y -> x * (y +2);; | |||
''val foo : int -> int -> int = <fun>'' | |||
'''let''' foo = '''fun''' x y -> x * (y +2);; | |||
''val foo : int -> int -> int = <fun>'' | |||
=== Procedury rekurencyjne === | |||
<p align="justify"> | |||
Procedury mogą być rekurencyjne. | |||
Musimy to jednak jawnie określić dodając słowo kluczowe <tt>rec</tt>: | |||
</p> | |||
<definicja> ::= <u>let</u> <u>rec</u> <identyfikator> {<identyfikator>}<sup>*</sup> <u>=</u> <wyrażenie> | |||
{{przyklad|[Procedury rekurencyjne]||}} | |||
'''let''' '''rec''' silnia n = | |||
'''if''' n < 2 '''then''' 1 '''else''' n * silnia (n - 1);; | |||
| |||
silnia 6;; | |||
''- : int = 720'' | |||
| |||
'''let rec''' fib n = | |||
'''if''' n < 2 '''then''' n '''else''' fib (n - 1) + fib (n - 2);; | |||
| |||
fib 10 - fib 7;; | |||
''- : int = 42'' | |||
{{uwaga||uwaga_A|Sens wyrażeń postaci <tt>'''if ... then ... else'''</tt> wyjaśniamy poniżej.}} | |||
<p align="justify"> | |||
Dodanie słówka <tt>rec</tt> powoduje, że definiowana procedura jest obecna w środowisku, w którym później będzie obliczana jej treść. | |||
Podobnie jak w przypadku definicji innych wartości, możemy równocześnie definiować kilka procedur, używając słowa kluczowego <tt>and</tt>. | |||
Jest to przydatne, gdy piszemy procedury wzajemnie rekurencyjne. | |||
</p> | |||
{{przyklad|[Procedury wzajemnie rekurencyjne]||}} | |||
'''let rec''' f n = | |||
'''if''' n < 2 '''then''' n '''else''' f (n-1) + g n | |||
'''and''' g n = | |||
'''if''' n <= 1 '''then''' 1 '''else''' n * f (n-1);; | |||
| |||
f 4 + f 2 - (f 3 + g 3);; | |||
''- : int = 42'' | |||
==Definicje lokalne== | ==Definicje lokalne== | ||
| Linia 239: | Linia 453: | ||
<wyrażenie> ::= <definicja> <u>in</u> <wyrażenie> | <wyrażenie> ::= <definicja> <u>in</u> <wyrażenie> | ||
Zakres definicji jest ograniczony do wyrażenia po <tt>in</tt>. | Zakres definicji jest ograniczony do wyrażenia po <tt>'''in'''</tt>. | ||
Na podstawie aktualnego środowiska tworzone jest tymczasowe środowisko, do którego wstawiane są wszystkie stałe zdefiniowane przed <tt>'''in'''</tt>. | |||
Tak utworzone środowisko jest używane tylko na potrzeby obliczenia wyrażenia po <tt>'''in'''</tt>. | |||
{{przyklad|[Definicje lokalne]||}} | {{przyklad|[Definicje lokalne]||}} | ||
| Linia 247: | Linia 463: | ||
'''and''' s = x *. x | '''and''' s = x *. x | ||
'''in''' pi *. s;; | '''in''' pi *. s;; | ||
''val pow : float -> float = <fun>'' | |||
pow 4.0;; | pow 4.0;; | ||
''- : float = 50.24'' | ''- : float = 50.24'' | ||
'''let''' pitagoras x y = | '''let''' pitagoras x y = | ||
'''let''' square x = x * x | '''let''' square x = x * x | ||
'''in''' | '''in''' | ||
square x + square y;; | square x + square y;; | ||
''val pitagoras : int -> int -> int = <fun>'' | |||
pitagoras 3 4;; | pitagoras 3 4;; | ||
''- : int = 25'' | ''- : int = 25'' | ||
| Linia 258: | Linia 479: | ||
==Wartości logiczne i wyrażenia warunkowe== | ==Wartości logiczne i wyrażenia warunkowe== | ||
Wartości typu <tt>bool</tt> to wartości logiczne: <tt>true</tt> i <tt>false</tt>. | <p align="justify"> | ||
Wartości typu <tt>bool</tt> to wartości logiczne. | |||
Składają się na nie dwie stałe: <tt>true</tt> i <tt>false</tt>. | |||
Z wartościami logicznymi związane są wyrażenia warunkowe postaci: | |||
</p> | |||
<wyrażenie> ::= <u>if</u> <wyrażenie> <u>then</u> <wyrażenie> <u>else</u> <wyrażenie> | <wyrażenie> ::= <u>if</u> <wyrażenie> <u>then</u> <wyrażenie> <u>else</u> <wyrażenie> | ||
Wartością pierwszego wyrażenia | <p align="justify"> | ||
Wartością pierwszego wyrażenia musi być wartość logiczna, a pozostałe dwa wyrażenia muszą | |||
być tego samego (lub uzgadnialnego) typu. | |||
Najpierw obliczane jest pierwsze wyrażenie. | |||
Jeżeli jest ono równe <tt>'''true'''</tt>, to obliczane jest drugie wyrażenie | |||
i jego wartość jest wartością całego wyrażenia. | |||
Jeżeli jest ono równe <tt>'''false'''</tt>, to obliczane jest trzecie wyrażenie | |||
i jego wartość jest wartością całego wyrażenia. | |||
</p> | |||
<p align="justify"> | |||
Obliczanie wyrażenia <tt>'''if''' ... '''then''' ... '''else'''</tt> jest w pewnym sensie leniwe | |||
-- obliczane jest tylko to, co niezbędne. | |||
Jeżeli warunek jest prawdziwy, to nie jest obliczany ostatni człon, a jeśli jest fałszywy, | |||
to nie jest obliczany drugi człon. | |||
Wyrażenie <tt>'''if''' ... '''then''' ... '''else'''</tt> jest formą specjalną, | |||
nie można go zdefiniować jako procedury, gdyż zawsze jeden z arumentów w ogóle nie jest obliczany. | |||
</p> | |||
{{uwaga||uwaga_B| Pojęciem ''typu'' będziemy dokładniej zajmować się dalej.}} | |||
{{przyklad|[Wartości logiczne i wyrażenia warunkowe]||}} | {{przyklad|[Wartości logiczne i wyrażenia warunkowe]||}} | ||
'''let''' abs x = | '''let''' abs x = | ||
'''if''' x < 0 '''then''' -x '''else''' x;; | '''if''' x < 0 '''then''' -x '''else''' x;; | ||
''val abs : int -> int = <fun>'' | |||
'''if''' x = 0.0 '''then''' "błąd: x = 0.0" '''else''' 1 /. x;; | |||
''error ...'' | '''if''' x = 0.0 '''then''' "błąd: x = 0.0" '''else''' 1.0 /. x;; | ||
''error ...'' | |||
'''if''' 42 '''then''' "ala" '''else''' "kot";; | |||
''error ...'' | |||
'''let''' '''rec''' silnia n = | '''let''' '''rec''' silnia n = | ||
'''if''' n < 2 '''then''' 1 '''else''' n * silnia (n - 1);; | '''if''' n < 2 '''then''' 1 '''else''' n * silnia (n - 1);; | ||
''val silnia : int -> int = <fun>'' | |||
silnia 7 / silnia 5;; | silnia 7 / silnia 5;; | ||
''- : int = 42'' | ''- : int = 42'' | ||
'''let''' '''rec''' fib n = | '''let''' '''rec''' fib n = | ||
'''if''' n < 2 '''then''' n '''else''' fib (n - 1) + fib (n - 2);; | '''if''' n < 2 '''then''' n '''else''' fib (n - 1) + fib (n - 2);; | ||
''val fib : int -> int = <fun>'' | |||
fib 10 - fib 7;; | fib 10 - fib 7;; | ||
''- : int = 42'' | ''- : int = 42'' | ||
<p align="justify"> | |||
Operatory logiczne <tt>&&</tt> i <tt>||</tt>, to odpowiedniokoniunkcja i alternatywa. Są to również formy specjalne | Operatory logiczne <tt>&&</tt> i <tt>||</tt>, to odpowiedniokoniunkcja i alternatywa. | ||
Są to również formy specjalne. | |||
Są one równoważne odpowiednim wyrażeniom warunkowym: | Są one równoważne odpowiednim wyrażeniom warunkowym: | ||
</p> | |||
x && y ≡ '''if''' x '''then''' y '''else''' false | |||
x || y ≡ '''if''' x '''then''' true '''else''' y | |||
<p align="justify"> | |||
Negacja, oznaczana przez <tt>'''not'''</tt> jest już zwykłą procedurą. | |||
</p> | |||
== Komentarze == | |||
<p align="justify"> | |||
Komentarze w Ocamlu umieszczamy w nawiasach postaci <tt>(* ... *)</tt>. | |||
Komentarze mogą pojawiać się wszędzie tam, gdzie mogą występować białe znaki. | |||
Komentarze można zagnieżdżać. | |||
</p> | |||
(* To jest komentarz. *) | |||
(* To też jest komentarz (* ale zagnieżdżony *). *) | |||
== | == Ćwiczenia == | ||
[[Programowanie funkcyjne/Podstawy/Ćwiczenia | | [[Programowanie funkcyjne/Podstawy/Ćwiczenia | Ćwiczenia]] | ||
Aktualna wersja na dzień 10:51, 5 wrz 2023
Wstęp
W każdym języku programowania mamy trzy rodzaje konstrukcji językowych:
- Podstawowe symbole -- Są to te byty występujące w języku (typy, wartości, operacje, relacje, procedury itp.), które są wbudowane w język i nie trzeba ich definiować.
- Sposoby konstrukcji -- Są to wszystkie te konstrukcje językowe, które pozwalają budować z prostszych elementów języka bardziej skomplikowane całości.
- Sposoby abstrakcji -- Są to te konstrukcje językowe, które pozwalają złożonym konstrukcjom nadawać nazwy. Nazwane konstrukcje mogą być dalej wykorzystywane tak, jak podstawowe symbole języka.
W językach imperatywnych, takich jak Pascal, C czy C++ przykładami symboli podstawowych są:
- typy proste, takie jak integer i float,
- stałe takie jak 0, 1, 2.3,
- operacje arytmetyczne, procedury implementowane przez biblioteki standardowe lub wbudowane (udostępniane przez bibliotekę run-time library).
Przykładami sposobów konstrukcji są:
- wyrażenia,
- typy złożone, takie jak tablice, struktury (rekordy) czy wskaźniki,
- instrukcje złożone, takie jak instrukcja warunkowa, pętle czy bloki instrukcji.
Do sposobów abstrakcji zaliczamy wszelkiego rodzaju definicje: definicje stałych, typów czy procedur. Niektóre konstrukcje językowe mogą łączyć ze sobą sposoby konstrukcji i abstrakcji. Najczęściej sposoby definicji zawierają w sobie sposoby konstrukcji. Na przykład, definicja procedury zwykle zawiera (jako ciało definiowanej procedury) blok instrukcji. Podobnie, niektóre sposoby konstrukcji wymagają, aby konstruowane całości były nazwane. Na przykład, w Pascalu typy argumentów procedur muszą być nazwane.
Czytelnikowi może w tej chwili wydawać się, że rozróżnianie sposobów konstrukcji i abstrakcji to dzielenie włosa na czworo. Jak zobaczymy w trakcie tego kursu, odróżnienie jednego od drugiego prowadzi do pewnych specyficznych konstrukcji językowych.
BNF
W kolejnych wykładach będziemy przedstawiać rozmaite konstrukcje językowe Ocamla. Do opisu składni tych konstrukcji, oprócz języka nieformalnego i przykładów, będziemy używać notacji BNF (ang. Backus–Naur form). Jest to rozszerzenie gramatyk bezkontekstowych, poręczne przy opisywaniu składni języków programowania. Notacja ta ma następującą postać:
- W BNF-ie definiujemy możliwe postaci rozmaitych konstrukcji składniowych. Konstrukcje te mają nazwy postaci: <konstrukcja>. Odpowiadają one nieterminalom w gramatykach bezkontekstowych.
- Opis składni składa się z szeregu reguł postaci <konstrukcja> ::= możliwa postać. Reguły te opisują możliwe postaci poszczególnych konstrukcji składniowych. Jeżeli dla danej konstrukcji mamy wiele reguł, to traktujemy je jak alternatywy. Reguły te odpowiadają produkcjom w gramatykach bezkontekstowych.
- Po prawej stronie reguł możemy używać następujących konstrukcji:
- podając tekst, który ma się pojawić dosłownie, będziemy go podkreślać, na przykład: słowo_kluczowe,
- nazw konstrukcji składniowych możemy używać również po prawej stronie reguł, na oznaczenie miejsc, w których się one pojawiają,
- chcąc opisać alternatywne postaci danej konstrukcji używamy pionowej kreski, ...|...,
- tekst umieszczony w kwadratowych nawiasach jest opcjonalny [...],
- dodatkowo, możemy używać nawiasów (wąsatych): {...},
- tekst umieszczony w nawiasach postaci {...}* może się powtarzać zero, jeden lub więcej razy,
- tekst umieszczony w nawiasach postaci {...}+ może się powtarzać jeden lub więcej razy.
Przykład [Adresy pocztowe]
BNF może byc użyty do opisywania składni najrozmaitszych rzeczy. Oto opis składni adresów pocztowych:
<adres> ::= <adresat> <adres lokalu> <adres miasta> <adres kraju> <adresat> ::= [W.P. | Sz.Pan.] <napis> , <adres lokalu> ::= <ulica> <numer> [ / <numer> ] [m <numer> |/ <numer> ] , <adres miasta> ::= [<kod>] <napis> <adres kraju> ::= [, <napis>] <kod> ::= <cyfra> <cyfra> - <cyfra> <cyfra> <cyfra> <cyfra> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 <numer> ::= <cyfra> [<numer>]
Specyfikacja ta oczywiście nie jest kompletna, gdyż nie definiuje czym jest napis.
Pamiętajmy, że czym innym jest symbol, a czym innym jego znaczenie (semantyka). BNF służy jedynie do opisu składni.
Przyrostowy tryb pracy
Kompilator Ocamla działa w sposób przyrostowy (inkrementacyjny), tzn. działa w cyklu powtarzając następujące czynności:
- wczytuje fragment programu,
- kompiluje go, dołączając do już skompilowanych fragmentów,
- wykonuje wprowadzony fragment.
Nazwa "tryb przyrostowy" bierze się stąd, że kompilator nie musi generować całego kodu od razu, lecz kod ten przyrasta z każdym cyklem.
Taki fragment programu, wprowadzany i kompilowany w jednym cyklu, będziemy nazywać jednostką kompilacji.
Wykonanie jednostki kompilacji może zarówno powodować obliczenie wartości, jak i definiowanie nowych pojęć.
Każda jednostka kompilacji musi być w Ocamlu zakończona przez ;;.
<program> ::= { <jednostka kompilacji> ;; }*
Podstawowe symbole Ocamla
Podstawowe symbole Ocamla obejmują m.inn:
- typy:
- bool -- wartości logiczne,
- int -- liczby całkowite,
- float -- liczby zmiennopozycyjne,
- char -- znaki,
- string -- napisy,
- stałe:
- logiczne (true i false),
- całkowite (np.: 0, 1, -2),
- zmiennopozycyjne (np.: 2.3, -3.4, 4.5e-7),
- znakowe (np.: 'a'),
- napisy (np. "ala ma kota").
- procedury:
- operacje arytmetyczne na liczbach całkowitych: +, -, *, /, mod,
- operacje arytmetyczne na liczbach zmiennopozycyjnych (zapisujemy je tak samo jak analogiczne operacje na liczbach całkowitych, ale dodając kropkę): +., -., *., /.,
- operacje logiczne:
- || (alternatywa),
- && (koniunkcja),
- not (negacja),
- sklejanie (konkatenacja) napisów ^,
- relacje (określone dla wszystkich typów): =, <=, >=, <, >, <>.
Wyrażenia
Najprostsza jednostka kompilacji i podstawowa konstrukcja programistyczna to wyrażenia. Wyrażenia budujemy w standardowy sposób za pomocą stałych, procedur i nawiasów. (Operacje arytmetyczne traktujemy tak jak inne procedury, z dokładnością do tego, że zapisujemy je infiksowo). Jedynym odstępstwem jest to, że argumenty procedur nie muszą być objęte nawiasami i pooddzielane przecinkami. Operacje, które standardowo zapisujemy infiksowo (np. operacje arytmetyczne) mają również postać infiksową. Rozróżniamy operacje arytmetyczne na liczbach całkowitych i rzeczywistych -- te ostatnie mają dodaną kropkę.
Przykład [Wyrażenia]
42;; - : int = 42 36 + 6;; - : int = 42 3 * 14;; - : int = 42 100 - 58;; - : int = 42 1 * 2 * 3 * 4 * 5 - ((6 + 7) * 8 * 9 / 12);; - : int = 42 silnia 7 / silnia 5;; - : int = 42 596.4 /. 14.2;; - : float = 42. "ala" ^ " ma " ^ "kota";; - : string = "ala ma kota"
Wszystko, czego potrzeba do budowy wyrażeń, to:
- stałe (liczbowe, napisy, lub nazwy stałych),
- zastosowanie procedur do argumentów,
- nawiasy.
Zauważmy, że procedury i ich argumenty są tu traktowane na równi -
takie symbole jak + czy * to po prostu nazwy stałych,
których wartościami są procedury wbudowane w język programowania,
a 123, 486.5, czy "ala" to stałe.
Składnia wyrażeń
<jednostka kompilacji> ::= <wyrażenie> | ...
<wyrażenie> ::= ( <wyrażenie> ) | { <wyrażenie> }+ | <operator unarny> <wyrażenie> |
<wyrażenie> <operator binarny> <wyrażenie> | <identyfikator> |
<stała całkowita> | <stała zmiennopozycyjna> | <stała napisowa> | ...
<operator unarny > ::= - | not | ...
<operator binarny> ::= + | +. | - | -. | * | *. | / | /. |
mod | || | && | = | < | <= | > | >= | ^ | ...
Powyższy opis składni nie jest jednoznaczny, tzn. ten sam program może zostać rozłożony składniowo na więcej niż jeden sposób (ale dzięki temu jest bardziej czytelny). Nie będziemy aż tak formalni. Zamiast tego ewentualne niejednoznaczności będziemy wyjaśniać w sposób opisowy.
Zastosowania procedur wiążą najsilniej, operatory unarne słabiej, a operatory binarne najsłabiej, przy czym zachowana jest tradycyjna kolejność wiązania operacji arytmetycznych.
Obliczanie wartości wyrażeń
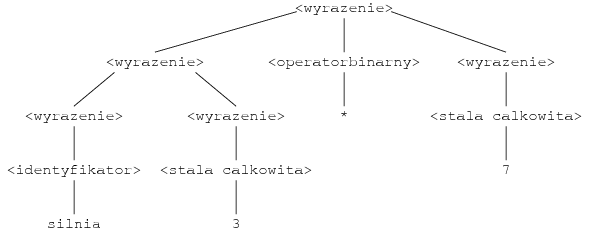
Efektem "działania" wyrażenia jest jego wartość. Rozkład składniowy danego wyrażenia możemy sobie przedstawić w postaci drzewa (tzw. drzewo wyprowadzenia). W liściach drzewa mamy stałe, a węzły wewnętrzne to procedury. Nawiasy wraz z priorytetami operatorów wyznaczają kształt takiego drzewa.
Przykład [Drzewo wyprowadzenia]
Oto drzewo wyprowadzenia dla wyrażenia silnia 3 * 7:
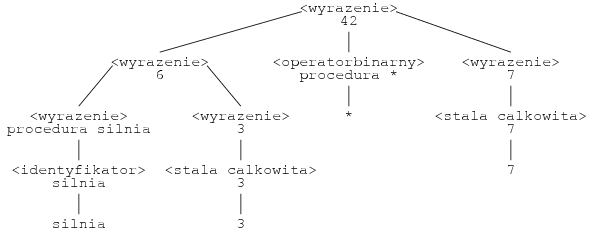
Wszystkie nazwane stałe są przechowywane w tzw. środowisku. Przyporządkowuje ono nazwom ich wartości. Jeśli w wyrażeniu występują nazwy stałych, to ich wartości są pobierane ze środowiska. Wyliczenie wartości wyrażenia możemy sobie wyobrazić jako udekorowanie drzewa wyprowadzenia wartościami, w kolejności od liści do korzenia. Wartość w korzeniu to wynik.
Przykład [Obliczanie wyrażenia]
Oto powyższe drzewo wyprowadzenia udekorowane wartościami:
Definicje stałych
Kolejną podstawową jednostką kompilacji jest definicja stałej.
<jednostka kompilacji> ::= <definicja> | ... <definicja> ::= let <identyfikator> = <wyrażenie> | ...
Definicji stałej nie da się wyrazić jako procedury ani wyrażenia, ponieważ zmienia ona środowisko. Dlatego też let jest nazywane formą specjalną. "Obliczenie" definicji wykonywane jest następująco:
- obliczana jest wartość wyrażenia tworzącego definicję,
- do środowiska wstawiany jest identyfikator, któremu przyporządkowywana jest wartość obliczonego wyrażenia.
Jeżeli symbol jest już w środowisku, to można przysłonić
go i nadać symbolowi nowe znaczenie.
W miarę jak będziemy poznawać kolejne konstrukcje językowe, będziemy go w miarę potrzeb rozszerzać.
Przykład [Definicje]
let a = 4;; val a : int = 4 let b = 5 * a;; val b : int = 20 let pi = 3.14;; val pi : float = 3.14 pi *. 4.0 *. 4.0;; val - : float = 50.24 let a = "ala";; val a : string = "ala"
Możliwe jest też równoczesne definiowanie wielu stałych. W takim przypadku najpierw obliczane są wszystkie wyrażenia, a następnie ich wartości są przypisywane w środowisku odpowiednim identyfikatorom.
<definicja> ::= let <identyfikator> = <wyrażenie>
{ and <identyfikator> = <wyrażenie> }^*
Przykład [Definicje równoczesne]
let a = 4 and b = 5;; val a : int = 4 val b : int = 5 let a = a + b and b = a * b;; val a : int = 9 val b : int = 20
Definicje procedur
Mamy tylko trzy podstawowe konstrukcje językowe:
- użycie wartości zdefiniowanej w środowisku (nie ważne liczby czy procedury),
- zastosowanie funkcji do argumentów (np. obliczenie mnożenia),
- definiowanie nowych wartości.
Jak wcześniej wspomnieliśmy, procedury są obywatelami pierwszej kategorii,
czyli równie dobrymi wartościami, jak wszystkie inne.
Wynika stąd, że:
- można definiować nazwane procedury (stałe proceduralne),
- procedura może być wartością wyrażenia,
- procedury mogą być argumentami i wynikami procedur (sic!).
Definicje nazwanych procedur mają następującą postać:
<definicja> ::= let <identyfikator> {<identyfikator>}+ = <wyrażenie>
Pierwszy z identyfikatorów to nazwa definiowanej procedury, a reszta to jej parametry formalne. Wyrażenie zaś to treść procedury. Określa ono wartość procedury, w zależności od wartości argumentów. Zwróćmy uwagę, że argumenty nie są otoczone nawiasami ani oddzielone przecinkami.
Przykład [Definicje nazwanych procedur]
let square x = x *. x;; val square : float -> float = <fun> let pow r = pi *. (square r);; val pow : float -> float = <fun> pow 4.0;; - : float = 50.24 let twice x = 2 * x;; val twice : int -> int = <fun> twice (twice 3);; - : int = 12 let mocium s = "mocium panie, " ^ s;; val mocium : string -> string = <fun> mocium (mocium "me wezwanie");; - : string = "mocium panie, mocium panie, me wezwanie"
Tak jak w przypadku innych wartości, gdy definiujemy procedurę kompilator odpowiada podając nam "typ" tej procedury. Typ ten zawiera typ argumentu i wyniku połączone strzałką. Na przykład, int -> int oznacza, że argument i wynik procedury są liczbami całkowitymi. W przypadku większej liczby argumentów zobaczymy większą liczbę strzałek. Typami procedur zajmiemy się dokładniej, gdy będziemy mówić o procedurach wyższych rzędów.
let plus x y = x + y;; val plus : int -> int -> int = <fun>
W momencie, gdy zastosujemy procedurę do jej argumentów, jej wartość jest obliczana w następujący sposób:
- obliczana jest procedura, którą należy zastosować i jej argumenty,
- na podstawie środowiska (w którym była definiowana procedura) tworzone jest tymczasowe środowisko, w którym dodatkowo parametrom formalnym są przyporządkowane wartości argumentów,
- w tym tymczasowym środowisku obliczane jest wyrażenie stanowiące treść procedury,
- wartość tak obliczonego wyrażenia jest wartością zastosowania procedury do argumentów.
-abstrakcja
Możemy też tworzyć procedury bez nazwy, tzn. takie procedury, które są wartością pewnego rodzaju wyrażeń, natomiast nie muszą pojawiać się w środowisku. Procedury takie możemy tworzyć za pomocą tzw. -abstrakcji.
Zauważmy, że funkcja, jako pojęcie matematyczne, nie musi mieć nazwy. Zwykle nadajemy funkcjom nazwy, gdyż tak jest poręcznie. Na przykład jest również dobrym opisem funkcji (której wartość jest o 1 większa od argumentu). -abstrakcja ma podobną postać. Składa się ona ze słowa kluczowego function, parametru formalnego funkcji, oraz wyrażenia określającego jej wartość.
<wyrażenie> ::= function <identyfikator> -> <wyrażenie>
Wartością takiego wyrażenia jest jednoargumentowa procedura bez nazwy. Narazie możemy przyjąć, że forma specjalna let definiująca procedurę z parametrami jest lukrem syntaktycznym pokrywającym wyrażenie function i definicję stałej.
Dostępna jest też skrócona forma zapisu nienazwanych procedur wieloargumentowych.
<wyrażenie> ::= fun {<identyfikator>}+ -> <wyrażenie>
Wyrażenie postaci:
fun x y z -> ...
jest równoważne:
function x -> function y -> function z -> ...
Oto alternatywna definicja procedur z poprzedniego przykładu.
Przykład [Alternatywne definicje procedur]
(function x -> x * (x + 1)) (2 * 3);; - : int = 42 let square = function x -> x *. x;; val square : float -> float = <fun> let pow = function r -> pi *. (square r);; val pow : float -> float = <fun> let twice = function x -> 2 * x;; val twice : int -> int = <fun> let foo = function x -> function y -> x * (y +2);; val foo : int -> int -> int = <fun> let foo = fun x y -> x * (y +2);; val foo : int -> int -> int = <fun>
Procedury rekurencyjne
Procedury mogą być rekurencyjne. Musimy to jednak jawnie określić dodając słowo kluczowe rec:
<definicja> ::= let rec <identyfikator> {<identyfikator>}* = <wyrażenie>
Przykład [Procedury rekurencyjne]
let rec silnia n = if n < 2 then 1 else n * silnia (n - 1);; silnia 6;; - : int = 720 let rec fib n = if n < 2 then n else fib (n - 1) + fib (n - 2);; fib 10 - fib 7;; - : int = 42
Dodanie słówka rec powoduje, że definiowana procedura jest obecna w środowisku, w którym później będzie obliczana jej treść. Podobnie jak w przypadku definicji innych wartości, możemy równocześnie definiować kilka procedur, używając słowa kluczowego and. Jest to przydatne, gdy piszemy procedury wzajemnie rekurencyjne.
Przykład [Procedury wzajemnie rekurencyjne]
let rec f n = if n < 2 then n else f (n-1) + g n and g n = if n <= 1 then 1 else n * f (n-1);; f 4 + f 2 - (f 3 + g 3);; - : int = 42
Definicje lokalne
Jeśli chcemy zdefiniować jakąś wartość lokalnie, używamy następującej postaci wyrażenia:
<wyrażenie> ::= <definicja> in <wyrażenie>
Zakres definicji jest ograniczony do wyrażenia po in. Na podstawie aktualnego środowiska tworzone jest tymczasowe środowisko, do którego wstawiane są wszystkie stałe zdefiniowane przed in. Tak utworzone środowisko jest używane tylko na potrzeby obliczenia wyrażenia po in.
Przykład [Definicje lokalne]
let pow x = let pi = 3.14 and s = x *. x in pi *. s;; val pow : float -> float = <fun> pow 4.0;; - : float = 50.24 let pitagoras x y = let square x = x * x in square x + square y;; val pitagoras : int -> int -> int = <fun> pitagoras 3 4;; - : int = 25
Wartości logiczne i wyrażenia warunkowe
Wartości typu bool to wartości logiczne. Składają się na nie dwie stałe: true i false. Z wartościami logicznymi związane są wyrażenia warunkowe postaci:
<wyrażenie> ::= if <wyrażenie> then <wyrażenie> else <wyrażenie>
Wartością pierwszego wyrażenia musi być wartość logiczna, a pozostałe dwa wyrażenia muszą być tego samego (lub uzgadnialnego) typu. Najpierw obliczane jest pierwsze wyrażenie. Jeżeli jest ono równe true, to obliczane jest drugie wyrażenie i jego wartość jest wartością całego wyrażenia. Jeżeli jest ono równe false, to obliczane jest trzecie wyrażenie i jego wartość jest wartością całego wyrażenia.
Obliczanie wyrażenia if ... then ... else jest w pewnym sensie leniwe -- obliczane jest tylko to, co niezbędne. Jeżeli warunek jest prawdziwy, to nie jest obliczany ostatni człon, a jeśli jest fałszywy, to nie jest obliczany drugi człon. Wyrażenie if ... then ... else jest formą specjalną, nie można go zdefiniować jako procedury, gdyż zawsze jeden z arumentów w ogóle nie jest obliczany.
Przykład [Wartości logiczne i wyrażenia warunkowe]
let abs x =
if x < 0 then -x else x;;
val abs : int -> int = <fun>
if x = 0.0 then "błąd: x = 0.0" else 1.0 /. x;;
error ...
if 42 then "ala" else "kot";;
error ...
let rec silnia n =
if n < 2 then 1 else n * silnia (n - 1);;
val silnia : int -> int = <fun>
silnia 7 / silnia 5;;
- : int = 42
let rec fib n =
if n < 2 then n else fib (n - 1) + fib (n - 2);;
val fib : int -> int = <fun>
fib 10 - fib 7;;
- : int = 42
Operatory logiczne && i ||, to odpowiedniokoniunkcja i alternatywa. Są to również formy specjalne. Są one równoważne odpowiednim wyrażeniom warunkowym:
x && y ≡ if x then y else false x || y ≡ if x then true else y
Negacja, oznaczana przez not jest już zwykłą procedurą.
Komentarze
Komentarze w Ocamlu umieszczamy w nawiasach postaci (* ... *). Komentarze mogą pojawiać się wszędzie tam, gdzie mogą występować białe znaki. Komentarze można zagnieżdżać.
(* To jest komentarz. *) (* To też jest komentarz (* ale zagnieżdżony *). *)