|
|
| (Nie pokazano 23 wersji utworzonych przez 4 użytkowników) |
| Linia 1: |
Linia 1: |
|
| |
|
| ==Interpolacja wielomianowa==
| | <!-- |
| | | Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php. |
| Teraz zajmiemy się zadaniami, w których
| | Niezb�dne rozszerzenia i modyfikacje oryginalnego latex2mediawiki |
| niewiadomymi są funkcje o wartościach rzeczywistych. Pierwszym z nich
| | wprowadzi� przykry@mimuw.edu.pl |
| jest zadanie interpolacji wielomianowej.
| | --> |
| | |
| Zadanie interpolacji, czyli poprowadzenia krzywej zadanego rodzaju przez zestaw
| |
| danych punktów, jest jednym z podstawowych zadań obliczeniowych. Stosuje się je
| |
| nagminnie w najróżniejszych dziedzinach życia, np.
| |
| * Na podstawie próbki sygnału dźwiękowego (to znaczy: ciągu wartości
| |
| amplitud sygnału zmierzonych w kolejnych odstępach czasu), odtworzyć jego przebieg.
| |
| * Przybliżyć wykres skomplikowanej (lub wręcz nieznanej) funkcji na
| |
| podstawie jej wartości uprzednio stablicowanych w wybranych punktach
| |
| * Interpolację stosuje się szczególnie chętnie w samej numeryce. Na przykład, idea
| |
| metody siecznych polega na tym, by funkcję, której miejsca zerowego szukamy,
| |
| przybliżyć prostą interpolującą tę funkcję w dwóch punktach. Metody numerycznego
| |
| całkowania oraz rozwiązywania równań różniczkowych także korzystają z
| |
| interpolacji.
| |
| | | |
| Niech <math>\displaystyle D\subsetR</math> i niech <math>\displaystyle F</math> będzie pewnym zbiorem funkcji
| | =Uwarunkowanie układu równań liniowych= |
| <math>\displaystyle f:D\toR</math>. Niech <math>\displaystyle x_0,x_1,\ldots,x_n</math> będzie ustalonym zbiorem
| |
| parami różnych punktów z <math>\displaystyle D</math>, zwanych później ''węzłami''.
| |
| | |
| Powiemy, że wielomian <math>\displaystyle w</math> ''interpoluje'' funkcję <math>\displaystyle f\in F</math>
| |
| w węzłach <math>\displaystyle x_j</math>, gdy
| |
| | |
| <center><math>\displaystyle w(x_j)\,=\,f(x_j),\qquad 0\le j\le n.
| |
| </math></center>
| |
| | |
| Oznaczmy przez <math>\displaystyle \Pi_n</math> przestrzeń liniową wielomianów stopnia
| |
| co najwyżej <math>\displaystyle n</math> o współczynnikach rzeczywistych,
| |
| | |
| <center><math>\displaystyle \Pi_n\,=\,\{\,w(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0:\;
| |
| a_j\inR, 0\le j\le n\,\}.
| |
| </math></center>
| |
| | |
| Zadanie znalezienia wielomianu interpolującego zadane wartości, nazywamy
| |
| zadaniem interpolacji Lagrange'a.
| |
| | |
| {{twierdzenie|Istnienie i jednoznaczność zadania interpolacji Lagrange'a||
| |
|
| |
| Dla dowolnej funkcji <math>\displaystyle f:D\toR</math> istnieje
| |
| dokładnie jeden wielomian <math>\displaystyle w_f\in\Pi_n</math> interpolujący <math>\displaystyle f</math>
| |
| w węzłach <math>\displaystyle x_j</math>, <math>\displaystyle 0\le j\le n</math>.
| |
| }}
| |
| | |
| {{dowod|||
| |
| Wybierzmy w <math>\displaystyle \Pi_n</math> dowolną bazę wielomianów
| |
| <math>\displaystyle \varphi_j</math>, <math>\displaystyle 0\le j\le n</math>,
| |
| | |
| <center><math>\displaystyle \Pi_n\,=\, \mbox{span} \{\,\varphi_0,\varphi_1,\ldots,\varphi_n\,\}.
| |
| </math></center>
| |
| | |
| Wtedy każdy wielomian z <math>\displaystyle \Pi_n</math> można jednoznacznie przedstawić
| |
| w postaci rozwinięcia względem wybranej bazy. Warunkiem koniecznym
| |
| i dostatecznym na to, aby wielomian
| |
| <math>\displaystyle w_f(\cdot)=\sum_{j=0}^n c_j\varphi_j(\cdot)</math>
| |
| interpolował <math>\displaystyle f</math> jest spełnienie układu <math>\displaystyle n+1</math> równań liniowych
| |
| | |
| <center><math>\displaystyle \sum_{j=0}^n c_j\varphi_j(x_i)\,=\,f(x_i),\qquad 0\le i\le n,
| |
| </math></center>
| |
| | |
| z <math>\displaystyle n+1</math> niewiadomymi <math>\displaystyle c_j</math>, który w postaci macierzowej wygląda
| |
| następująco:
| |
| | |
| <center><math>\displaystyle
| |
| \left(\begin{array} {cccc}
| |
| \varphi_0(x_0) & \varphi_1(x_0) & \cdots & \varphi_n(x_0) \\
| |
| \varphi_0(x_1) & \varphi_1(x_1) & \cdots & \varphi_n(x_1) \\
| |
| \vdots \\
| |
| \varphi_0(x_n) & \varphi_1(x_n) & \cdots & \varphi_n(x_n)
| |
| \end{array} \right)\left(\begin{array} {c}
| |
| c_0 \\ c_1 \\ \vdots \\ c_n \end{array} \right)\,=\,
| |
| \left(\begin{array} {c}
| |
| f(x_0) \\ f(x_1) \\ \vdots \\ f(x_n) \end{array} \right).
| |
| </math></center>
| |
| | |
| Aby wykazać, że układ ten ma jednoznaczne rozwiązanie wystarczy,
| |
| aby wektor zerowy był jedynym rozwiązaniem układu jednorodnego.
| |
| Rzeczywiście, układ jednorodny odpowiada interpolacji danych zerowych,
| |
| <math>\displaystyle f(x_i)=0</math>, <math>\displaystyle \forall i</math>. Istnienie niezerowego rozwiązania byłoby
| |
| więc równoważne istnieniu niezerowego wielomianu stopnia nie większego
| |
| od <math>\displaystyle n</math>, który miałby <math>\displaystyle n+1</math> różnych zer <math>\displaystyle x_i</math>, co jest niemożliwe.
| |
| }}
| |
| | |
| Zadanie znalezienia dla danej funkcji <math>\displaystyle f</math> jej wielomianu interpolacyjnego
| |
| stopnia co najwyżej <math>\displaystyle n</math> jest więc dobrze zdefiniowane, tzn. rozwiązanie
| |
| istnieje i jest wyznaczone jednoznacznie. Zauważmy, że wielomian
| |
| interpolacyjny <math>\displaystyle w_f</math> jako taki nie może być wynikiem obliczeń w naszym
| |
| modelu obliczeniowym, możemy natomiast wyznaczyć jego współczynniki
| |
| <math>\displaystyle c_j</math> w wybranej bazie.
| |
| | |
| {{definicja|||
| |
| Niech <math>\displaystyle (\varphi_j)_{j=0}^n</math> będzie bazą w przestrzeni
| |
| <math>\displaystyle \Pi_n</math> wielomianów stopnia co najwyżej <math>\displaystyle n</math>. Zadanie
| |
| interpolacji wielomianowej polega na obliczeniu dla danej funkcji <math>\displaystyle f</math>
| |
| współ\-czyn\-ni\-ków <math>\displaystyle c_j</math> takich, że wielomian
| |
| | |
| <center><math>\displaystyle
| |
| w_f(\cdot)\,=\,\sum_{j=0}^n c_j\varphi_j(\cdot)
| |
| </math></center>
| |
| | |
| interpoluje <math>\displaystyle f</math> w punktach <math>\displaystyle x_j</math>, <math>\displaystyle 0\le j\le n</math>.
| |
| }}
| |
| | |
| ===Uwarunkowanie===
| |
| | |
| Danymi w zadaniu interpolacji są zarówno wartości interpolowanej funkcji, jak i
| |
| węzły interpolacji. Traktując węzły jako sztywno zadane parametry
| |
| zadania i dopuszczając jedynie zaburzenia wartości funkcji, można pokazać, że
| |
| jeśli zamiast <math>\displaystyle f</math> rozpatrzyć jej zaburzenie <math>\displaystyle f+\Delta f</math>, gdzie <math>\displaystyle |\Delta f| \leq
| |
| \epsilon</math>, to
| |
| | |
| <center><math>\displaystyle |w_f(x) - w_{f+\Delta f}(x)| \leq \mbox{cond(x,f)} |w_f(x)|\epsilon,
| |
| </math></center>
| |
| | |
| gdzie
| |
| | |
| <center><math>\displaystyle \mbox{cond(x,f)} = \frac{\sum_{j=0}^n |l_j(x) f(x_j)|}{|p_n(x)|} \geq 1.
| |
| </math></center>
| |
| | |
| ===Wybór bazy wielomianowej===
| |
| | |
| Jak już wiemy, zadanie interpolacji Lagrange'a sprowadza się do rozwiązania
| |
| układu równań liniowych. Okazuje się, że w zależności od ''wyboru sposobu | |
| reprezentacji'' naszego wielomianu (czyli od wyboru bazy wielomianowej <math>\displaystyle (\varphi_j)_{j=0}^n</math>), układ
| |
| ten może być albo bardzo łatwy do rozwiązania, albo --- bardzo trudny. Co
| |
| więcej, jego rozwiązanie w arytmetyce <math>\displaystyle fl_\nu</math> może napotykać na większe bądź
| |
| mniejsze trudności (w zależności np. od uwarunkowania macierzy układu, który
| |
| musimy rozwiązać).
| |
| | |
| W naturalny sposób powstaje więc problem wyboru "wygodnej" bazy w <math>\displaystyle \Pi_n</math>.
| |
| Rozpatrzymy trzy bazy: Lagrange'a, potęgową i Newtona.
| |
| | |
| ====Baza Lagrange'a (kanoniczna)====
| |
| | |
| Zdefiniujmy dla <math>\displaystyle 0\le j\le n</math> wielomiany
| |
| | |
| <center><math>\displaystyle
| |
| l_j(x)\,=\,\frac
| |
| {(x -x_0)(x -x_1)\cdots(x -x_{j-1})(x -x_{j+1})\cdots(x -x_n)}
| |
| {(x_j-x_0)(x_j-x_1)\cdots(x_j-x_{j-1})(x_j-x_{j+1})\cdots(x_j-x_n)}.
| |
| </math></center>
| |
| | |
| Zauważmy, że każdy z <math>\displaystyle l_j</math> jest stopnia dokładnie <math>\displaystyle n</math> oraz
| |
| | |
| <center><math>\displaystyle l_j(x_i)\,=\,\left\{\,\begin{array} {ll}
| |
| 0 & \quad i\ne j, \\ 1 & \quad i=j. \end{array} \right.
| |
| </math></center>
| |
| | |
| Stąd łatwo widać, że wielomiany te stanowią bazę w <math>\displaystyle \Pi_n</math>,
| |
| którą nazywamy bazą Lagrange'a. Macierz układu zadania interpolacji
| |
| jest w takim wypadku identycznością i w konsekwencji <math>\displaystyle c_j=f(x_j)</math>, <math>\displaystyle \forall j</math>.
| |
| Wielomian interpolacyjny dla funkcji <math>\displaystyle f</math> można więc
| |
| zapisać jako
| |
|
| |
|
| <center><math>\displaystyle w_f(\cdot)\,=\,\sum_{j=0}^n f(x_j)l_j(\cdot).
| | {{powrot |Metody numeryczne | do strony głównej |
| </math></center> | | przedmiotu <strong>Metody numeryczne</strong>}} |
|
| |
|
| Koszt kombinatoryczny rozwiązania zadania interpolacji jest przy tym
| | Zajmiemy się wrażliwością układu równań na zaburzenia danych: prawej strony i |
| zerowy.
| | współczynników macierzy układu. Jak zobaczymy na poniższym przykładzie, bywają |
| | równania, które są mało podatne na zaburzenia danych (a więc: dobrze |
| | uwarunkowane) oraz równania, które są szalenie wrażliwe na zaburzenia, a więc |
| | źle uwarunkowane. Jak wkrótce się przekonamy, czułość danego układu równań na |
| | zaburzenia da się precyzyjnie scharakteryzować, a cecha ta nie tylko będzie |
| | miała wpływ na jakość rozwiązań możliwych do uzyskania w arytmetyce skończonej |
| | precyzji, ale także na efektywność [[MN08|metod iteracyjnych]] rozwiązywania układów równań liniowych, w których są tysięce (lub więcej) niewiadomych. |
|
| |
|
| Przypuśćmy, że chcielibyśmy obliczyć wartość wielomianu
| | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> |
| interpolacyjnego <math>\displaystyle w_f</math> w punkcie <math>\displaystyle x</math> różnym od <math>\displaystyle x_j</math>, <math>\displaystyle 0\le j\le n</math>.
| | <span style="font-variant:small-caps;">Przykład: Uwarunkowanie układu dwóch równań liniowych</span> |
| Podstawiając
| | <div class="solution" style="margin-left,margin-right:3em;"> |
|
| |
|
| <center><math>\displaystyle w_j\,=\,\frac 1 {(x_j-x_0)(x_j-x_1)\cdots(x_j-x_{j-1})
| | Rozwiązanie układu dwóch równań liniowych można przedstawić w formie graficznej: |
| (x_j-x_{j+1})\cdots(x_j-x_n)}
| | jest to punkt przecięcia się dwóch prostych wyznaczonych przez dane |
| </math></center>
| | współczynniki i wyrazy prawej strony. |
|
| |
|
| oraz <math>\displaystyle p_n(x)=(x-x_0)\cdots(x-x_n)</math> mamy '''pierwszy wzór barycentryczny'''
| | [[Image:MNlinearcond.png|thumb|550px|center|Rozważmy pewien nieosobliwy układ dwóch równań |
| | liniowych. Ma on dokładnie jedno rozwiązanie, na rysunku oznaczone kolorem czerwonym. Co się stanie, gdy trochę zaburzymy prawą stronę takiego układu?]] |
|
| |
|
| <center><math>\displaystyle
| | [[Image:MNlinearcond1.png|thumb|550px|center|Wykresy zaburzonych prostych mogą zająć jedną z |
| w_f(x)\,=\,p_n(x)\sum_{j=0}^n\frac{w_jf(x_j)}{x-x_j},
| | zaznaczonych łososiowym kolorem pozycji.]] |
| </math></center>
| |
|
| |
|
| i ostatecznie dostajemy tzw. '''drugi wzór barycentryczny''' na wielomian interpolacyjny,
| | [[Image:MNlinearcond2.png|thumb|550px|center|Obszar, gdzie mogą znaleźć się rozwiązania zaburzonego |
| | układu, zaznaczyliśmy na czerwono. Jest on, kolokwialnie rzecz ujmując, z |
| | grubsza tak |
| | wielki jak wielkie były zaburzenia, co zgodne jest z typową intuicją "człowieka |
| | z zewnątrz".]] |
|
| |
|
| <center><math>\displaystyle w_f(x)\,=\,\frac{\sum_{j=0}^n q_j(x)f(x_j)}{\sum_{j=0}^n q_j(x)},
| | [[Image:MNlinearcond3.png|thumb|550px|center|Jednak bywają |
| </math></center> | | równania, wrażliwe jak mimoza na nawet delikatne zaburzenia danych. Takie |
| | równanie właśnie widzimy na rysunku: jego cechą szczególną jest to, że tym razem |
| | proste, choć wciąż przecinają się dokładnie w jednym punkcie, są <strong>prawie</strong> |
| | równoległe.]] |
|
| |
|
| gdzie <math>\displaystyle q_j(x)=w_j/(x-x_j)</math>. W ostatniej równości wykorzystaliśmy fakt,
| | [[Image:MNlinearcond4.png|thumb|550px|center|Bierzemy zaburzenia takie same, jak poprzednio. Wykresy zaburzonych prostych mogą zająć jedną z zaznaczonych łososiowym kolorem pozycji.]] |
| że <math>\displaystyle p_n(x)\equiv (\sum_{j=0}^n q_j(x))^{-1}</math>, co łatwo widzieć, rozpatrując
| |
| zadanie interpolacji funkcji <math>\displaystyle f\equiv 1</math>.
| |
|
| |
|
| Dla wielu układów węzłów wagi <math>\displaystyle w_j</math> są zadane jawnymi wzorami, np. dla węzłów
| | [[Image:MNlinearcond5.png|thumb|550px|center|Tym razem obszar niepewności, gdzie mogą być |
| równoodległych (niezależnie od tego na jakim odcinku!) wagi w ''drugim'' wzorze
| | rozwiązania naszego zaburzonego układu, jest <strong>gigantyczny</strong>!]] |
| barycentrycznym wynoszą po prostu
| |
|
| |
|
| <center><math>\displaystyle w_j = (-1)^j \begin{pmatrix} n \\ j \end{pmatrix} .
| | </div></div> |
| </math></center> | |
|
| |
|
| Można pokazać, że wartość <math>\displaystyle \widetilde{w_f(x)}</math> wielomianu iterpolacyjnego obliczona
| | A więc równania liniowe mogą, choć nie muszą, być bardzo podatne na zaburzenia |
| w arytmetyce <math>\displaystyle fl_\nu</math> według pierwszego algorytmu barycentrycznego spełnia
| | danych. Gdy zamiast prawej strony, zaburzymy wyrazy macierzy układu, może nawet |
| | okazać się, że dostaniemy układ równań sprzecznych (czy możesz podać przykład?) |
|
| |
|
| <center><math>\displaystyle
| | Aby przedstawić ogólną teorię zaburzeń dla układów równań liniowych, musimy mieć |
| \widetilde{w_f(x)} = p_n(x) \sum_{j=0}^n\frac{w_j}{x-x_j}f(x_j)(1+\epsilon_j),
| | narzędzia do pomiaru błędu rozwiązań, a także zaburzeń danych zadania: czyli |
| </math></center>
| | macierzy i wektora prawej strony. Temu będą służyć normy. |
|
| |
|
| gdzie <math>\displaystyle |\epsilon_j| \leq 5(n+1)</math>, a więc jest to algorytm numerycznie poprawny.
| | ==Normy wektorowe i macierzowe== |
| Zachowanie drugiej postaci wzoru barycentrycznego w arytmetyce <math>\displaystyle fl_\nu</math> jest nieco
| |
| bardziej skomplikowane, ale w typowych zadaniach .
| |
|
| |
|
| ====Baza potęgowa (naturalna)==== | | Aby badać odległość między rozwiązaniem dokładnym układu równań a jego |
| | wartością przybliżoną uzyskaną np. algorytmem eliminacji Gaussa, będziemy |
| | posługiwać się normami wektorów |
| | <math>x = (x_j)_{j=1}^n\in R^n</math> |
| | i macierzy <math>A = (a_{i,j})_{i,j=1}^n \in R^{n\times n}</math>. |
| | Najczęściej używanymi normami wektorowymi będą |
| | <strong>normy <math>p</math>-te</strong>, |
|
| |
|
| Znacznie prościej można obliczyć wartość wielomianu interpolacyjnego,
| | <center><math>\| x\|\,=\,\| x\|_p\,=\, |
| (a także jego pochodnych), gdy jest on dany w najczęściej używanej | | \left(\sum_{j=1}^n |x_j|^p\right)^{1/p}, |
| bazie potęgowej, <math>\displaystyle \varphi_j(x)=x^j</math>, <math>\displaystyle \forall j</math>. Jeśli bowiem
| | \qquad 1\le p< +\infty</math>,</center> |
|
| |
|
| <center><math>\displaystyle w_f(x)\,=\,a_0+a_1x+\cdots+ a_nx^n,
| | oraz |
| </math></center>
| |
|
| |
|
| to również
| | <center><math>\| x\|_\infty\,=\,\lim_{p\to +\infty}\| x\|_p\,=\, |
| | | \max_{1\le j\le n}|x_j|. |
| <center><math>\displaystyle w_f(x)\,=\,(\cdots(a_nx+a_{n-1})x+a_{n-2})x+\cdots+a_1)x+a_0, | |
| </math></center> | | </math></center> |
|
| |
|
| co sugeruje zastosowanie następującego ''schematu Hornera''
| | W szczególności, norma <math>||\cdot||_2</math> jest dobrze nam znaną normą euklidesową wektora. |
| do obliczenia <math>\displaystyle w_f(x)</math>:
| |
| | |
| {{algorytm|Algorytm Hornera||
| |
| <pre>
| |
| | |
| <math>\displaystyle v_n = a_n;</math>
| |
| for (j<nowiki>=</nowiki>n-1; j ><nowiki>=</nowiki> 0 ; j--)
| |
| <math>\displaystyle v_j\, = \,v_{j+1}\cdot x\,+\,a_j</math>;
| |
| </pre>}}
| |
|
| |
|
| Po wykonaniu tego algorytmu <math>\displaystyle w_f(x)=v_0</math>. Schemat Hornera wymaga wykonania
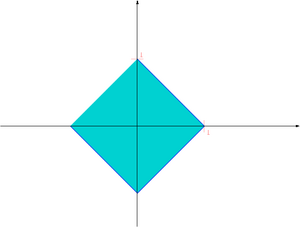
| | [[Image:MNball1.png|thumb|300px|center|Kula jednostkowa w normie <math>||\cdot||_1</math> w <math>R^2</math>]] |
| tylko <math>\displaystyle n</math> mnożeń i <math>\displaystyle n</math> dodawań. Ma on również głębszy sens,
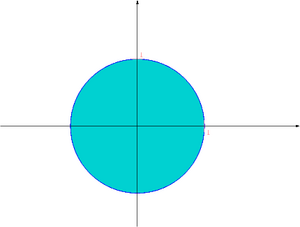
| | [[Image:MNball2.png|thumb|300px|center|Kula jednostkowa w normie <math>||\cdot||_2</math> w <math>R^2</math>]] |
| bo jego produktem ubocznym mogą być także wartości pochodnych naszego wielomianu w <math>\displaystyle x</math>.
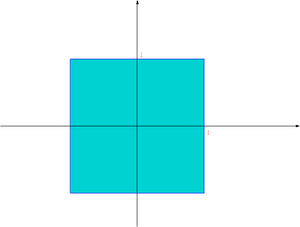
| | [[Image:MNballinf.png|thumb|300px|center|Kula jednostkowa w normie <math>||\cdot||_\infty</math> w <math>R^2</math>]] |
| Algorytm Hornera okazuje się optymalny. Każdy
| |
| inny algorytm obliczający dokładną wartość wielomianu znając
| |
| jego współczynniki wymaga wykonania co najmniej <math>\displaystyle n</math> mnożeń i <math>\displaystyle n</math>
| |
| dodawań. Algorytm Hornera jest też numerycznie poprawny.
| |
|
| |
|
| Zauważmy jednak, że w przypadku bazy potęgowej macierz
| | Normą macierzową jest norma Frobeniusa |
| <math>\displaystyle (x_i^j)_{i,j=0}^n</math> układu zadania interpolacji jest pełna. Jest to tzw.
| |
| ''macierz Vandermonde'a''. Obliczenie współczynników wielomianu
| |
| interpolacyjnego w bazie potęgowej bezpośrednio z tego układu, stosując
| |
| jedną ze znanych nam już metod, kosztowałoby rzędu <math>\displaystyle n^3</math> operacji
| |
| arytmetycznych. Co gorsza, w często spotykanym przypadku, gdy węzły interpolacji
| |
| są równoodległe, ta macierz jest bardzo źle uwarunkowana!
| |
|
| |
|
| ====Baza Newtona==== | | <center><math>\|A\|_F\,=\,\sqrt{\sum_{i,j=1}^n |a_{i,j}|^2}</math>,</center> |
|
| |
|
| Rozwiązaniem pośrednim, które łączy prostotę obliczenia
| | a także <strong>normy indukowane</strong> przez normy wektorowe (np. przez |
| współczynników z prostotą obliczenia wartości <math>\displaystyle w_f(x)</math> i ewentualnie jego
| | normy <math>p</math>-te) |
| pochodnych
| |
| jest wybór bazy Newtona,
| |
|
| |
|
| <center><math>\displaystyle \aligned p_0(x) &= 1, \\ | | <center><math>\|A\|\,=\,\sup_{x\ne 0}\frac{\|A x\|}{\| x\|}\,=\, |
| p_j(x) &= (x-x_0)(x-x_1)\cdots(x-x_{j-1}),\qquad 1\le j\le n.
| | \sup_{\|x\|=1}\|A x\|</math></center> |
| \endaligned</math></center> | |
|
| |
|
| W tym przypadku współczynniki rozwinięcia wielomianu interpolacyjnego
| | Jeśli norma macierzowa jest indukowana przez normę wektorową, |
| będziemy oznaczać przez <math>\displaystyle b_j</math>,
| | to dla dowolnego wektora mamy |
|
| |
|
| <center><math>\displaystyle w_f\,=\,\sum_{j=0}^n b_jp_j. | | <center><math>\|A x\|\,\le\,\|A\|\| x\|. |
| </math></center> | | </math></center> |
|
| |
|
| Zwróćmy od razu uwagę na ważną własność bazy Newtona. Jeśli
| | Przypomnijmy, że w przestrzeniach liniowych skończenie wymiarowych |
| <math>\displaystyle w_{f,j}\in\Pi_j</math> jest wielomianem interpolacyjnym dla funkcji <math>\displaystyle f</math> opartym | | (a więc także w <math>R^n</math> i w przestrzeni macierzy wymiaru <math>n\times n</math>) |
| na węzłach <math>\displaystyle x_0,x_1,\ldots,x_j</math>, <math>\displaystyle 0\le j\le n</math>, to <math>\displaystyle w_{f,0}=b_0</math> oraz
| | każde dwie normy są równoważne. To znaczy, że jeśli mamy dwie |
| | normy <math>\|\cdot\|</math> i <math>\|\cdot\|'</math> w przestrzeni skończenie wymiarowej |
| | <math>X</math>, to istnieją stałe <math>0<K_1\le K_2<\infty</math> takie, że |
|
| |
|
| <center><math>\displaystyle | | <center><math>K_1\,\|x\|\,\le\,\|x\|'\,\le\,K_2\,\|x\|,\qquad\forall x\in X</math></center> |
| w_{f,j}\,=\,w_{f,j-1}\,+\,b_jp_j,\qquad 1\le j\le n.
| |
| </math></center> | |
|
| |
|
| Wartość <math>\displaystyle w_f(x)</math> można obliczyć stosując prostą modyfikację
| | W szczególności dla <math>x\in R^n</math> mamy |
| algorytmu Hornera:
| |
|
| |
|
| {{algorytm|Algorytm Hornera dla bazy Newtona|| | | <center><math>\begin{align} \| x\|_\infty &\le & \| x\|_1\,\le\, |
| <pre> | | n\,\| x\|_\infty, \\ |
| | \| x\|_\infty &\le & \| x\|_2\,\le\, |
| | \sqrt{n}\,\| x\|_\infty,\\ |
| | \frac 1{\sqrt n}\,\| x\|_1 &\le & \| x\|_2\,\le\, |
| | \| x\|_1, |
| | \end{align}</math></center> |
|
| |
|
| <math>\displaystyle v_n = b_n;</math> | | a dla <math>A=(a_{i,j})_{i,j=1}^n</math> mamy |
| for (j<nowiki>=</nowiki>n-1; j ><nowiki>=</nowiki> 0 ; j--)
| |
| <math>\displaystyle v_j\, = \,v_{j+1}\cdot (x-x_j)\,+\,b_j</math>;
| |
| </pre>}}
| |
|
| |
|
| Ponadto układ równań zadania interpolacji jest trójkątny dolny, o specyficznej
| | <center><math> |
| strukturze, dzięki czemu można stworzyć elegancki algorytm, który teraz
| | \|A\|_2\, \le\, \|\,|A|\,\|_2 \,\le\, \|A\|_E |
| przedstawimy.
| | \,\le\, \sqrt n\, \|A\|_2</math>,</center> |
|
| |
|
| ===Algorytm różnic dzielonych=== | | gdzie <math>|A|=(|a_{i,j}|)_{i,j=1}^n</math>. |
|
| |
|
| ''Różnicę dzieloną'' funkcji <math>\displaystyle f</math> opartą na różnych węzłach
| | Dla macierzy |
| <math>\displaystyle t_0,t_1,\ldots,t_s</math>, gdzie <math>\displaystyle s\ge 1</math>, definiuje się indukcyjnie jako | | <math>A=(a_{i,j})_{i.j=1}^n\in R^{n\times n}</math> mamy |
|
| |
|
| <center><math>\displaystyle | | <center><math>\|A\|_\infty \,=\, \max_{1\le i\le n}\sum_{j=1}^n |a_{i,j}| |
| f(t_0,t_1,\ldots,t_s)\,=\,\frac
| |
| {f(t_1,t_2,\ldots,t_s)\,-\,f(t_0,t_1,\ldots,t_{s-1})}{t_s\,-\,t_0}.
| |
| </math></center> | | </math></center> |
|
| |
|
| Zachodzi następujące ważne twierdzenie.
| | oraz |
|
| |
|
| {{twierdzenie|O różnicach dzielonych||
| | <center><math>\|A\|_1 \,=\, \|A^T\|_\infty \,=\, |
|
| | \max_{1\le j\le n}\sum_{i=1}^n |a_{i,j}|</math></center> |
| Współczynniki <math>\displaystyle b_j</math> wielomianu
| |
| interpolacyjnego Newtona dla danej funkcji <math>\displaystyle f</math> dane są przez
| |
| różnice dzielone <math>\displaystyle f</math> w węzłach <math>\displaystyle x_0,x_1,\ldots,x_j</math>, tzn.
| |
|
| |
|
| <center><math>\displaystyle b_j\,=\,f(x_0,x_1,\ldots,x_j),\qquad 0\le j\le n.
| | Dowód tego faktu zostawiamy jako [[MN07LAB|ćwiczenie]]. |
| </math></center>
| |
|
| |
|
| }}
| | ==Uwarunkowanie układu równań liniowych== |
| | |
| {{dowod|||
| |
| Dla <math>\displaystyle 0\le i\le j\le n</math>, oznaczmy przez <math>\displaystyle w_{i,j}</math>
| |
| wielomian z <math>\displaystyle \Pi_{j-i}</math> interpolujący <math>\displaystyle f</math> w węzłach
| |
| <math>\displaystyle x_i,x_{i+1},\ldots,x_j</math>. Wtedy ma miejsce następująca równość (<math>\displaystyle i<j</math>):
| |
| | |
| <center><math>\displaystyle
| |
| w_{i,j}(x)\,=\,\frac{(x-x_i)w_{i+1,j}(x)\,-\,(x-x_j)w_{i,j-1}(x)}
| |
| {x_j\,-\,x_i}, \qquad\forall x.
| |
| </math></center>
| |
| | |
| Aby ją pokazać wystarczy, że prawa strona tej równości, którą
| |
| oznaczymy przez <math>\displaystyle v(x)</math>, przyjmuje wartości <math>\displaystyle f(x_s)</math> dla <math>\displaystyle x=x_s</math>,
| |
| <math>\displaystyle i\le s\le j</math>. Rzeczywiście, jeśli <math>\displaystyle i+1\le s\le j-1</math> to
| |
|
| |
|
| <center><math>\displaystyle v(x_s)\,=\,\frac{(x_s-x_i)f(x_s)-(x_s-x_j)f(x_s)}{x_j-x_i} | | Wyprowadzimy teraz wynik świadczący o tym, jak zaburzenie względne danych |
| \,=\,f(x_s).
| | przenosi się na błąd względny wyniku rozwiązania <math>x^*</math> układu równań liniowych <math>Ax=b</math>. |
| </math></center> | |
|
| |
|
| Ponadto
| | {{twierdzenie|O uwarunkowaniu układu równań|O uwarunkowaniu układu równań| |
|
| |
|
| <center><math>\displaystyle v(x_i)\,=\,\frac{-(x_i-x_j)}{x_j-x_i}f(x_i)\,=\,f(x_i), | | Niech <math>E</math> i <math>e</math> będą zaburzeniami |
| </math></center> | | odpowiednio macierzy <math>A</math> i wektora <math>b</math> na poziomie względnym <math>\epsilon</math>, tzn. |
|
| |
|
| oraz podobnie <math>\displaystyle v(x_j)=f(x_j)</math>. Stąd <math>\displaystyle v</math> jest wielominem
| | <center><math>\frac{\|E\|}{\|A\|} \,\le\,\epsilon \qquad \mbox{i} \qquad \frac{\|e\|}{\|b\|} \,\le\,\epsilon</math></center> |
| z <math>\displaystyle \Pi_{j-i}</math> interpolującym <math>\displaystyle f</math> w węzłach <math>\displaystyle x_s</math>, <math>\displaystyle i\le s\le j</math>,
| |
| czyli <math>\displaystyle w_{i,j}=v</math>.
| |
|
| |
|
| Dalej postępujemy indukcyjnie ze względu na stopień <math>\displaystyle n</math>
| | Jeśli |
| wielomianu interpolacyjnego. Dla <math>\displaystyle n=0</math> mamy oczywiście <math>\displaystyle b_0=f(x_0)</math>.
| |
| Niech <math>\displaystyle n\ge 1</math>. Ponieważ, jak łatwo zauważyć,
| |
|
| |
|
| <center><math>\displaystyle w_{0,n}(x)\,=\,w_{0,n-1}(x)+b_n p_n(x), | | <center><math>\epsilon\cdot \mbox{cond} (A)\,<\,1</math>,</center> |
| </math></center> | |
|
| |
|
| z założenia indukcyjnego mamy <math>\displaystyle b_j=f(x_0,\ldots,x_j)</math> dla
| | to układ zaburzony <math>(A+E) x=( b+ e)</math> ma jednoznaczne |
| <math>\displaystyle 0\le j\le n-1</math>. Aby pokazać podobną równość dla <math>\displaystyle b_n</math>, | | rozwiązanie <math>z^*</math> spełniające |
| zauważmy, że
| |
|
| |
|
| <center><math>\displaystyle w_{0,n}(x)\,=\,\frac{(x-x_0)w_{1,n}(x)-(x-x_n)w_{0,n-1}(x)}{x_n-x_0}. | | <center><math>\frac{\| z^*- x^*\|}{\| x^*\|} \; \le \; \frac{2\, \mbox{cond} (A)}{1-\epsilon \mbox{cond} (A)} \epsilon</math>,</center> |
| </math></center> | |
|
| |
|
| Zauważmy teraz, że <math>\displaystyle b_n</math> jest współczynnikiem przy <math>\displaystyle x^n</math>
| | gdzie definiujemy <strong>współczynnik uwarunkowania układu</strong> |
| w wielomianie <math>\displaystyle w_{0,n}</math>. Z założenia indukcyjnego wynika, że
| |
| współczynniki przy <math>\displaystyle x^{n-1}</math> w wielomianach <math>\displaystyle w_{1,n}</math> i <math>\displaystyle w_{0,n-1}</math>
| |
| są ilorazami różnicowymi opartymi odpowiednio na węzłach
| |
| <math>\displaystyle x_1,\ldots,x_n</math> i <math>\displaystyle x_0,\ldots,x_{n-1}</math>. Stąd
| |
|
| |
|
| <center><math>\displaystyle b_n\,=\,\frac{f(x_1,\ldots,x_n)-f(x_0,\ldots,x_{n-1})}{x_n-x_0} | | <center><math>\mbox{cond} (A) = ||A||\cdot ||A^{-1}||</math></center> |
| \,=\,f(x_0,x_1,\ldots,x_n),
| |
| </math></center> | |
|
| |
|
| co kończy dowód.
| |
| }} | | }} |
|
| |
|
| Różnicę dzieloną <math>\displaystyle f(x_0,x_1,\ldots,x_n)</math> można łatwo
| | Zauważmy najpierw, że zachodzi |
| obliczyć na podstawie wartości <math>\displaystyle f(x_j)</math>, <math>\displaystyle 0\le j\le n</math>,
| |
| budując następującą tabelkę:
| |
| | |
| <center><math>\displaystyle \begin{array} {llllll}
| |
| x_0 & f(x_0) \\
| |
| x_1 & f(x_1) & f(x_0,x_1) \\
| |
| x_2 & f(x_2) & f(x_1,x_2) & f(x_0,x_1,x_2) \\
| |
| \vdots &\vdots &\vdots &\vdots &\ddots \\
| |
| x_n & f(x_n) & f(x_{n-1},x_n) & f(x_{n-2},x_{n-1},x_n) &\cdots
| |
| & f(x_0,x_1,\ldots,x_n).\end{array}
| |
| </math></center>
| |
| | |
| Zauważmy przy tym, że "po drodze" obliczamy | |
| <math>\displaystyle f(x_i,x_{i+1},\ldots,x_j)</math> dla wszystkich <math>\displaystyle 0\le i < j\le n</math>, a więc
| |
| w szczególności również interesujące nas różnice dzielone
| |
| <math>\displaystyle f(x_0,x_1,\ldots,x_j)</math>. Stąd i z Twierdzenia o różnicach dzielonych
| |
| natychmiast wynika algorytm obliczania współczynników
| |
| <math>\displaystyle b_j</math> wielomianu interpolacyjnego w bazie Newtona.
| |
| Po wykonaniu następującego algorytmu,
| |
| | |
| {{algorytm|Metoda różnic dzielonych||
| |
| <pre>
| |
|
| |
|
| for (j <nowiki>=</nowiki> 0; j <<nowiki>=</nowiki> n; j++)
| | {{lemat|Neumanna o otwartości zbioru macierzy odwracalnych|Neumanna o otwartości zbioru macierzy odwracalnych| |
| <math>\displaystyle b_j</math> <nowiki>=</nowiki> <math>\displaystyle f(x_j)</math>;
| |
| for (j <nowiki>=</nowiki> 0; j <<nowiki>=</nowiki> n; j++)
| |
| for (k <nowiki>=</nowiki> n; k ><nowiki>=</nowiki> j; k--)
| |
| <math>\displaystyle b_j</math> <nowiki>=</nowiki> <math>\displaystyle (b_k-b_{k-1})/(x_k - x_{k-j})</math>;
| |
| </pre>}}
| |
|
| |
|
| współczynniki <math>\displaystyle b_j</math> na końcu algorytmu zawierają wspólczynniki wielomianu
| | Jeśli <math>F</math> jest macierzą |
| interpolacyjnego w bazie Newtona. Czy gdybyś zobaczył ten algorytm na samym
| | taką, że <math>\|F\|<1</math>, to macierz <math>(I-F)</math> jest nieosobliwa oraz |
| początku tego wykładu, to zgadłbyś, do czego może służyć?!
| |
|
| |
|
| <div class="thumb tright"><div><flash>file=roznicedzielone.swf</flash><div.thumbcaption>Działanie algorytmu różnic dzielonych</div></div></div> | | <center><math>\| (I-F)^{-1} \|\,\le\,\frac{1}{1-\|F\|}</math></center> |
|
| |
|
| Okazuje się, że przy realizacji w <math>\displaystyle fl_\nu</math>
| |
| algorytmu różnic dzielonych istotną rolę odgrywa porządek
| |
| węzłów. Można pokazać, że algorytm liczenia <math>\displaystyle f(t_0,\ldots,t_n)</math>
| |
| jest numerycznie poprawny ze względu na dane interpolacyjne
| |
| <math>\displaystyle f^{(i)}(t_j)</math>, o ile węzły są uporządkowane nierosnąco lub
| |
| niemalejąco.
| |
|
| |
| ===Przypadek węzłów wielokrotnych===
| |
|
| |
| Uogólnieniem rozpatrzonego zadania interpolacji jest zadanie
| |
| interpolacji ''Hermite'a''. Zakładamy, że oprócz (różnych)
| |
| węzłów <math>\displaystyle x_j</math> dane są również ich krotności <math>\displaystyle n_j</math>, <math>\displaystyle 0\le j\le k</math>,
| |
| przy czym <math>\displaystyle \sum_{j=0}^k n_j=n+1</math>. Należy skonstruować wielomian
| |
| <math>\displaystyle w_f\in\Pi_n</math> taki, że
| |
|
| |
| <center><math>\displaystyle w_f^{(i)}(x_j)\,=\,f^{(i)}(x_j)\qquad \mbox{ dla } \quad
| |
| 0\le i\le n_j-1, 0\le j\le k.
| |
| </math></center>
| |
|
| |
| Oczywiście zakładamy przy tym, że odpowiednie pochodne funkcji
| |
| <math>\displaystyle f</math> istnieją.
| |
|
| |
| {{lemat|||
| |
| Zadanie interpolacji Hermite'a ma jednoznaczne
| |
| rozwiązanie.
| |
| }} | | }} |
|
| |
|
| {{dowod||| | | {{dowod||| |
| Istnienie i jednoznaczność rozwiązania można
| | Rzeczywiście, gdyby <math>(I-F)</math> była osobliwa, to istniałby niezerowy |
| uzasadnić tak samo jak w przypadku węzłów jednokrotnych.
| | wektor <math>x</math> taki, że <math>(I-F) x=0</math>, co implikuje |
| Przedstawiając wielomian w dowolnej bazie otrzymujemy układ <math>\displaystyle n+1</math>
| | <math>\|F x\|/\| x\|=1</math> i w konsekwencji <math>\|F\|\ge 1</math>. Aby |
| równań z <math>\displaystyle n+1</math> niewiadomymi, który dla zerowej prawej strony ma
| | pokazać oszacowanie normy macierzy <math>(I-F)^{-1}</math> zauważmy, że |
| jedynie rozwiązanie zerowe. Inaczej bowiem istniałby wielomian niezerowy
| |
| stopnia nie większego niż <math>\displaystyle n</math>, który miałby zera o łącznej krotności
| |
| większej niż <math>\displaystyle n</math>.
| |
| }}
| |
| | |
| Nas oczywiście interesuje konstrukcja wielomianu <math>\displaystyle w_f</math>. W tym celu
| |
| ustawimy węzły <math>\displaystyle x_j</math> w ciąg
| |
|
| |
|
| <center><math>\displaystyle (\bar x_0,\bar x_1,\ldots,\bar x_n)\,=\, | | <center><math>\begin{align} 1 &= \|I\|\,=\,\|(I-F)(I-F)^{-1}\| \\ &\ge & |
| (\underbrace{x_0,\ldots,x_0}_{n_0},\underbrace{x_1,\ldots,x_1}_{n_1},
| | \|(I-F)^{-1}\|\,-\,\|F\|\,\|(I-F)^{-1}\| \\ |
| \ldots,\underbrace{x_k,\ldots,x_k}_{n_k})
| | &= (1-\|F\|)\,\|(I-F)^{-1}\|, |
| </math></center>
| | \end{align}</math></center> |
| | |
| i zdefiniujemy uogólnioną bazę Newtona w <math>\displaystyle \Pi_n</math> jako
| |
| | |
| <center><math>\displaystyle \aligned p_0(x) &= 1, \\
| |
| p_j(x) &= (x-\bar x_0)(x-\bar x_1)\cdots (x-\bar x_{j-1}),
| |
| \qquad 1\le j\le n.
| |
| \endaligned</math></center> | |
| | |
| Uogólnimy również pojęcie różnicy dzielonej na węzły
| |
| powtarzające się kładąc
| |
| | |
| <center><math>\displaystyle f(\bar x_i,\bar x_{i+1},\ldots,\bar x_j)\,=\,
| |
| \frac{f^{(j-i)}(\bar x_i)}{(j-i)!}
| |
| </math></center>
| |
| | |
| dla <math>\displaystyle \bar x_i=\bar x_{i+1}=\cdots=\bar x_j</math>, oraz
| |
| | |
| <center><math>\displaystyle f(\bar x_i,\bar x_{i+1},\ldots,\bar x_j)\,=\,\frac
| |
| {f(\bar x_{i+1},\ldots,\bar x_j)-f(\bar x_i,\ldots,x_{j-1})}
| |
| {\bar x_j-\bar x_i}
| |
| </math></center>
| |
| | |
| dla <math>\displaystyle \bar x_i\ne\bar x_j</math>. Zauważmy, że przy tej definicji
| |
| różnice <math>\displaystyle f(\bar x_i,\ldots,\bar x_j)</math> możemy łatwo obliczyć
| |
| stosując schemat podobny do tego z przypadku węzłów jednokrotnych.
| |
| | |
| {{twierdzenie|||
| |
| Współczynniki <math>\displaystyle b_j</math> wielomianu interpolacyjnego
| |
| Hermite'a w bazie Newtona,
| |
| | |
| <center><math>\displaystyle w_f(\cdot)\,=\,\sum_{j=0}^n b_jp_j(\cdot),
| |
| </math></center>
| |
| | |
| dane są przez odpowiednie różnice dzielone, tzn.
| |
| | |
| <center><math>\displaystyle b_j\,=\,f(\bar x_0,\bar x_1,\ldots,\bar x_j),\qquad 0\le j\le n.
| |
| </math></center> | |
|
| |
|
| | skąd już wynika dowodzona nierówność. |
| }} | | }} |
|
| |
|
| {{dowod||| | | {{dowod|twierdzenia o uwarunkowaniu|twierdzenia o uwarunkowaniu| |
| Dowód przeprowadzimy podobnie jak dla węzłów
| |
| jednokrotnych. Niech <math>\displaystyle w_{i,j}\in\Pi_{j-i}</math> oznacza wielomian
| |
| interpolacyjny Hermite'a oparty na (być może powtarzających się)
| |
| węzłach <math>\displaystyle \bar x_i,\bar x_{i+1},\ldots,\bar x_j</math>.
| |
| To znaczy, <math>\displaystyle w_{i,j}</math> interpoluje <math>\displaystyle f</math> w węzłach <math>\displaystyle x_s</math> takich, że
| |
| <math>\displaystyle x_s</math> występuje w ciągu <math>\displaystyle \bar x_i,\ldots\bar x_j</math>, a jego krotność
| |
| jest liczbą powtórzeń <math>\displaystyle x_s</math> w tym ciągu.
| |
|
| |
|
| Zauważmy najpierw, że dla <math>\displaystyle \bar x_i\ne\bar x_j</math> zachodzi znany nam
| | Po podstawieniu <math>F=-A^{-1}E</math> mamy teraz |
| już wzór,
| |
|
| |
|
| <center><math>\displaystyle | | <center><math>\|F\|\,\le\,\|A^{-1}\|\,\|E\|\,\le\,\epsilon\|A\|\,\|A^{-1}\|\,<\,1</math>,</center> |
| w_{i,j}(x)\,=\,\frac{(x-\bar x_i)w_{i+1,j}(x)\,-\,
| |
| (x-\bar x_j)w_{i,j-1}(x)} {\bar x_j\,-\,\bar x_i}.
| |
| </math></center> | |
|
| |
|
| Rzeczywiście, oznaczmy przez <math>\displaystyle v(x)</math> prawą stronę powyższej równości.
| | co wobec równości <math>A+E=A(I+A^{-1}E)</math> daje, że macierz <math>(A+E)</math> |
| Dla <math>\displaystyle k</math> mniejszego od krotności danego węzła <math>\displaystyle x_s</math>
| | jest nieosobliwa i układ zaburzony ma jednoznaczne rozwiązanie |
| w ciągu <math>\displaystyle \bar x_i,\ldots\bar x_j</math>, mamy
| | <math>z^*</math>. Przedstawmy to rozwiązanie w postaci |
| <math>\displaystyle w_{i+1,j}^{(k-1)}(x_s)=w_{i,j-1}^{(k-1)}(x_s)</math>, a ponieważ | | <math>z^*= x^*+( z^*- x^*)</math>. Rozpisując układ |
| | zaburzony i wykorzystując równość <math>A x^*= b</math> otrzymujemy, |
| | że <math>(A+E)( z^*- x^*)= e\,-\,E x^*</math>, czyli |
|
| |
|
| <center><math>\displaystyle \aligned v^{(k)}(x)&=\frac{k\,(w_{i+1,j}^{(k-1)}(x)-w_{i,j-1}^{(k-1)}(x))} | | <center><math>z^*- x^* \,=\, (I+A^{-1}E)^{-1}A^{-1}( e-E x^*)</math>,</center> |
| {\bar x_j-\bar x_i} \\ && \qquad +\,
| |
| \frac{(x-\bar x_i)w_{i+1,j}^{(k)}(x)-(x-\bar x_j)w_{i,j-1}^{(k)}(x)}
| |
| {\bar x_j-\bar x_i},
| |
| \endaligned</math></center>
| |
|
| |
|
| to
| | a stąd |
|
| |
|
| <center><math>\displaystyle v^{(k)}(x_s) \,=\, | | <center><math>\begin{align} \| z^*- x^*\| &\le & \|(I+A^{-1}E)^{-1}\|\,\|A^{-1}\| \, |
| \frac{(x_s-\bar x_i)w_{i+1,j}^{(k)}(x_s)- | | (\| e\|+\|E\|\,\| x^*\| \\ |
| (x_s-\bar x_j)w_{i,j-1}^{(k)}(x_s)} {\bar x_j-\bar x_i}.
| | &\le & \frac{\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} |
| </math></center> | | \epsilon\left(\| b\|+\|A\|\,\| x^*\|\right) \\ |
| | &\le & \frac{\|A\|\,\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} |
| | 2\epsilon\cdot\| x^*\|, |
| | \end{align}</math></center> |
|
| |
|
| Korzystając z tego wzoru sprawdzamy, że <math>\displaystyle v</math> spełnia odpowiednie
| | co kończy dowód. |
| warunki interpolacyjne, a stąd <math>\displaystyle w_{i,j}=v</math>.
| |
| | |
| Dalej postępujemy indukcyjnie ze względu na <math>\displaystyle n</math>. Dla <math>\displaystyle n=0</math>
| |
| mamy <math>\displaystyle b_0=f(x_0)</math>. Dla <math>\displaystyle n\ge 1</math> wystarczy pokazać, że
| |
| <math>\displaystyle b_n\,=\,f(\bar x_0,\bar x_1,\ldots,\bar x_n)</math>. W tym celu
| |
| rozpatrzymy dwa przypadki.
| |
| | |
| Jeśli <math>\displaystyle \bar x_0=\bar x_n</math> to mamy jeden węzeł <math>\displaystyle x_0</math>
| |
| o krotności <math>\displaystyle n+1</math>. Wielomian interpolacyjny jest wtedy postaci
| |
| | |
| <center><math>\displaystyle w_f(x)\,=\,\sum_{j=0}^n \frac{f^{(j)}(x_0)}{j!}(x-x_0)^j,
| |
| </math></center>
| |
| | |
| a stąd <math>\displaystyle b_n=f^{(n)}(x_0)//(n!)=f(\underbrace{x_0,\ldots,x_0}_{n+1})</math>.
| |
| Jeśli zaś <math>\displaystyle \bar x_0\ne\bar x_j</math> to równość
| |
| <math>\displaystyle b_n\,=\,f(\bar x_0,\bar x_1,\ldots,\bar x_n)</math> wynika z wcześniej
| |
| wyprowadzonych wzorów oraz z założenia indukcyjnego.
| |
| }} | | }} |
|
| |
|
| {{uwaga|||
| | Gdy więc np. <math>\epsilon \mbox{cond} (A) \leq \frac{1}{2}</math>, [[#O uwarunkowaniu układu równań|oszacowanie błędu rozwiązania układu zaburzonego]] możemy |
| Zauważmy, ze pojęcie różnicy dzielonej
| | zastąpić czytelniejszym (choć mniej precyzyjnym) |
| formalnie zdefiniowaliśmy jedynie dla ciągu węzłów postaci
| |
| <math>\displaystyle x_0,\ldots,x_0,x_1,\ldots,x_1,\ldots,x_k,\ldots,x_k</math>, gdzie | |
| <math>\displaystyle x_j</math> są parami różne. Tą definicję można rozszerzyć do
| |
| dowolnego ciągu węzłów. Można bowiem powiedzieć, że
| |
| <math>\displaystyle f(t_0,t_1,\ldots,t_n)</math> jest współczynnikiem przy <math>\displaystyle x^n</math> wielomianu
| |
| <math>\displaystyle w_{t_0,\ldots,t_n}\in\Pi_n</math> interpolującego <math>\displaystyle f</math> w węzłach <math>\displaystyle t_j</math>
| |
| (uwzględniając krotności). Równoważnie, | |
|
| |
|
| <center><math>\displaystyle f(t_0,t_1,\ldots,t_n)\,=\,\frac{w^{(n)}_{t_0,\ldots,t_n}}{n!}. | | <center><math>\frac{\| z^*- x^*\|}{\| x^*\|} \leq 4 \, \mbox{cond} (A) \, \epsilon</math></center> |
| </math></center> | |
|
| |
|
| }}
| | Octave i MATLAB mają wbudowane funkcje wyznaczające normy wektorów i macierzy |
| | <div style="margin: 1em; padding:1em; color: #006; background-color:#fcfcfc;"><pre>N = 3; |
| | x = [1:N]' |
| | A = pascal(N) |
| | norm(A,1) |
| | norm(x,2) |
| | norm(A,Inf) |
| | </pre></div> |
| | |
| | a także funkcje wyznaczające uwarunkowanie macierzy, przy czym Octave liczy |
| | tylko uwarunkowanie w normie <math>||\cdot||_2</math>: |
|
| |
|
| ===Błąd interpolacji=== | | <div style="margin: 1em; padding:1em; color: #006; background-color:#fcfcfc;"><pre>cond(A) |
| | | </pre></div> |
| Gdy mamy do czynienia z funkcją, która jest
| |
| "skomplikowana" to często dobrze jest zastąpić ją | |
| funkcją "prostszą". Mówimy wtedy o ''aproksymacji
| |
| (przybliżaniu) funkcji''. Funkcję musimy również
| |
| aproksymać wtedy, gdy nie jesteśmy w stanie uzyskać
| |
| pełnej o niej informacji. Na przykład, gdy funkcja
| |
| reprezentuje pewien proces fizyczny to często zdarza się,
| |
| że dysponujemy jedynie ciągiem próbek, czyli wartościami
| |
| tej funkcji w pewnych punktach. Jasne jest, że chcielibyśmy
| |
| przy tym, aby błąd aproksymacji był możliwie mały.
| |
| | |
| Z tego punktu widzenia, intepolacja wielomianowa może być
| |
| traktowana jako jeden ze sposobów aproksymacji funkcji,
| |
| opartym na próbkowaniu. Naturalnym staje się więc pytanie
| |
| o błąd takiej aproksymacji.
| |
| | |
| Niech <math>\displaystyle x_0,x_1,\ldots,x_n</math> będą (niekoniecznie różnymi)
| |
| węzłami należącymi do pewnego (być może nieskończonego)
| |
| przedziału <math>\displaystyle D\subsetR</math>. Dla danej funkcji <math>\displaystyle f:D\toR</math>, przez
| |
| <math>\displaystyle w_f</math> rozważamy, tak jak w całym wykładzie, wielomian
| |
| interpolacyjny stopnia co najwyżej <math>\displaystyle n</math> interpolujący <math>\displaystyle f</math>
| |
| w zadanych węzłach. W przypadku węzłów wielokrotnych
| |
| jest to oczywiście wielomian interpolacyjny Hermite'a; gdy węzły są jednokrotne,
| |
| mamy do czynienia z interpolacją Lagrange'a.
| |
| | |
| {{lemat|Postać błędu interpolacji||
| |
| | | |
| Dla dowolnego punktu
| | W [http://www.netlib.org/lapack LAPACKu] służy do tego funkcja <code style="color: #903">DGECON</code>. Zadanie wyznaczania uwarunkowania macierzy jest zadaniem bardzo intensywnym numerycznie. Problem, czy da się je wyznaczyć z dobrą dokładnością kosztem niższym niż wyznaczenie macierzy odwrotnej i jej normy, jest wciąż otwarty. |
| <math>\displaystyle \bar x\in D</math> błąd interpolacji w <math>\displaystyle \bar x</math> wyraża się
| |
| wzorem
| |
| | |
| <center><math>\displaystyle
| |
| f(\bar x)-w_f(\bar x)\,=\,(\bar x-x_0)(\bar x-x_1)
| |
| \cdots(\bar x-x_n)f(x_0,x_1,\ldots,x_n,\bar x).
| |
| </math></center>
| |
| | |
| Jeśli ponadto <math>\displaystyle f\in C^{(n+1)}(D)</math>, czyli pochodna
| |
| <math>\displaystyle f^{(n+1)}</math> w <math>\displaystyle D</math> istnieje i jest ciągła, to
| |
| | |
| <center><math>\displaystyle f(\bar x)-w_f(\bar x)\,=\,(\bar x-x_0)(\bar x-x_1)
| |
| \cdots(\bar x-x_n)\frac{f^{(n+1)}(\xi)}{(n+1)!},
| |
| </math></center>
| |
| | |
| gdzie <math>\displaystyle \xi=\xi(\bar x)</math> jest pewnym punktem należącym do
| |
| najmniejszego przedziału zawierającego punkty
| |
| <math>\displaystyle x_0,x_1,\ldots,x_n,\bar x</math>.
| |
| }}
| |
| | |
| {{dowod|||
| |
| Możemy założyć, że <math>\displaystyle \bar x</math> nie jest
| |
| żadnym z węzłów <math>\displaystyle x_j</math>, <math>\displaystyle 0\le j\le n</math>. Niech
| |
| <math>\displaystyle \bar w_f\in\Pi_{n+1}</math> będzie wielomianem interpolacyjnym
| |
| funkcji <math>\displaystyle f</math> opartym na węzłach <math>\displaystyle x_0,\ldots,x_n</math> i dodatkowo
| |
| na węźle <math>\displaystyle \bar x</math>. Mamy wtedy
| |
| | |
| <center><math>\displaystyle \bar w_f(x)\,=\,w_f(x)\,+\,(x-x_0)(x-x_1)\cdots(x-x_n)
| |
| f(x_0,x_1,\ldots,x_n,\bar x),
| |
| </math></center>
| |
|
| |
|
| a ponieważ z warunku interpolacyjnego
| | W praktyce obliczeniowej trafiają się zarówno układy dobrze uwarunkowane, jak i |
| <math>\displaystyle f(\bar x)=\bar w_f(\bar x)</math>, to mamy też pierwszą równość w lemacie.
| | macierze, których uwarunkowanie może być patologicznie duże (np. takie macierze |
| | są chlebem powszednim osób rozwiązujących równania różniczkowe). |
|
| |
|
| Aby pokazać drugą część lematu, rozpatrzmy funkcję
| | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> |
| <math>\displaystyle \psi:D\toR</math>, | | <span style="font-variant:small-caps;">Przykład: Macierz Hilberta</span> |
| | <div class="solution" style="margin-left,margin-right:3em;"> |
|
| |
|
| <center><math>\displaystyle \aligned \lefteqn{\psi(x) \;=\; f(x)-\bar w_f(x)} \\ | | Przykładem macierzy o uwarunkowaniu wyjątkowo szybko rosnącym z wymiarem jest m.in. <strong>macierz Hilberta</strong> <math>H_N = (h_{ij})_{i,j=1}^N</math>, gdzie |
| &= \, f(x)-w_f(x)-(x-x_0)(x-x_1)\cdots(x-x_n)
| | <center><math> |
| f(x_0,\ldots,x_n,\bar x).
| | h_{ij} = \frac{1}{i+j-1}</math></center> |
| \endaligned</math></center>
| |
|
| |
|
| Z warunków interpolacyjnych na <math>\displaystyle \bar w_f\in\Pi_{n+1}</math>
| | [[Image:MNhilbertmatrix.png|thumb|550px|center|Macierz Hilberta wymiaru 25. Kolor odpowiada rzędowi wielkości elementu macierzy, dokładniej, <math>\log(h_{ij})</math>. Jak widzisz, większość elementów tej macierzy jest równa prawie zero, a więc w konsekwencji kolumny macierzy są prawie liniowo zależne. ]] |
| wynika, że funkcja <math>\displaystyle \psi</math> ma punkty zerowe o łącznej
| |
| krotności co najmniej <math>\displaystyle n+2</math>. Wykorzystując twierdzenie
| |
| Rolle'a wnioskujemy stąd, że <math>\displaystyle \psi'</math> ma zera o łącznej
| |
| krotności co najmniej <math>\displaystyle n+1</math>, <math>\displaystyle \psi''</math> ma zera o łącznej
| |
| krotności co najmniej <math>\displaystyle n</math>, itd. W końcu funkcja
| |
| <math>\displaystyle \psi^{(n+1)}</math> zeruje się w co najmniej jednym punkcie
| |
| <math>\displaystyle \xi=\xi(\bar x)</math> należącym do najmniejszego przedziału
| |
| zawierającego <math>\displaystyle x_0,x_1,\ldots,x_n,\bar x</math>. Wobec tego, że
| |
| <math>\displaystyle w_f^{(n+1)}\equiv 0</math>, a <math>\displaystyle (n+1)</math>-sza pochodna wielomianu
| |
| <math>\displaystyle (x-x_0)\cdots(x-x_n)</math> wynosi <math>\displaystyle (n+1)!</math>, mamy
| |
|
| |
|
| <center><math>\displaystyle 0 \,=\, \psi^{(n+1)}(\xi)\,=\,f^{(n+1)}(\xi)-(n+1)! | | Taką macierz możemy wygenerować w Octave komendą <code style="color: #006">hilb(N)</code>. Jest to bardzo specyficzna macierz, co m.in. przejawia się tym, że uwarunkowanie macierzy Hilberta rośnie eksponencjalnie z <math>N</math>, <math>\mbox{cond} (H_N) \approx O(e^{3.5N})</math>: |
| f(x_0,\ldots,x_n,\bar x).
| |
| </math></center> | |
|
| |
|
| Stąd
| | <div style="font-family: monospace; white-space: pre; border-style: dashed; border-width: thin; border-color: black; margin: 1em; padding:1em; color: #444; background-color:#fdfdfd;"><realnowiki><realnowiki><nowiki>octave:2> cond(hilb(5)) |
| | | ans = 4.7661e+05 |
| <center><math>\displaystyle f(x_0,x_1,\ldots,x_n,\bar x)\,=\,
| | octave:3> cond(hilb(10)) |
| \frac{f^{(n+1)}(\xi)}{(n+1)!},
| | ans = 1.6025e+13 |
| </math></center>
| | octave:4> cond(hilb(15)) |
| | | ans = 3.7689e+17 |
| co kończy dowód.}}
| | octave:5> cond(hilb(20)) |
| | | ans = 7.1209e+19 |
| Zwykle interesuje nas nie tyle błąd w ustalonym punkcie
| | </nowiki></realnowiki></realnowiki></div> |
| <math>\displaystyle \bar x\in D</math>, ale na całym przedziale <math>\displaystyle D</math>. Zakładając
| |
| teraz, że przedział <math>\displaystyle D</math> jest domknięty, czyli
| |
| | |
| <center><math>\displaystyle D\,=\,[a,b]
| |
| </math></center>
| |
| | |
| dla pewnych <math>\displaystyle -\infty<a<b<+\infty</math>, błąd ten będziemy
| |
| mierzyć w normie ''jednostajnej'' (Czebyszewa). Dla
| |
| funkcji ciągłej <math>\displaystyle g:[a,b]\toR</math>, norma ta jest zdefiniowana
| |
| jako
| |
| | |
| <center><math>\displaystyle \|g\|_{ C([a,b])}\,=\,\max_{x\in D} |g(x)|.
| |
| </math></center>
| |
| | |
| Niech <math>\displaystyle F^r_M([a,b])</math>, gdzie <math>\displaystyle r\ge 0</math>, będzie klasą funkcji
| |
| | |
| <center><math>\displaystyle F^r_M([a,b])\,=\,\{\,f\in C^{(r+1)}([a,b]):\,
| |
| \|f^{(r+1)}\|_{ C([a,b])}\le M\,\},
| |
| </math></center>
| |
| | |
| gdzie <math>\displaystyle 0<M<\infty</math>. Mamy następujące twiedzenie.
| |
| | |
| {{twierdzenie|||
| |
| Załóżmy, że każdą funkcję
| |
| <math>\displaystyle f\in F^r_M([a,b])</math> aproksymujemy jej wielomianem
| |
| interpolacyjnym <math>\displaystyle w_f\in\Pi_r</math> opartym na <math>\displaystyle r+1</math>
| |
| węzłach <math>\displaystyle x_0,\ldots,x_r\in [a,b]</math>. Wtedy maksymalny
| |
| błąd takiej aproksymacji wynosi
| |
| | |
| <center><math>\displaystyle \aligned e(F^r_M([a,b]);x_0,x_1,\ldots,x_r) &=
| |
| \max_{f\in F^r_M([a,b])} \|f-w_f\|_{ C([a,b])} \\
| |
| &= \frac M{(r+1)!}\cdot
| |
| \max_{a\le x\le b}|(x-x_0)\cdots(x-x_r)|.
| |
| \endaligned</math></center>
| |
| | |
| }}
| |
| | |
| {{dowod|||
| |
| Oszacowanie górne wynika bezpośrednio
| |
| z Lematu o postaci błędu interpolacji, bowiem dla <math>\displaystyle f\in F^r_M([a,b])</math> mamy
| |
| | |
| <center><math>\displaystyle \aligned \|f-w_f\|_{ C([a,b])}&=\max_{a\le x\le b}|f(x)-w_f(x)| \\ | |
| &= \max_{a\le x\le b}|(x-x_0)\cdots(x-x_r)|
| |
| \frac{|f^{(r+1)}(\xi(x))|}{(r+1)!} \\
| |
| &\le & \frac{M}{(r+1)!}\max_{x\in D}|(x-x_0)\cdots(x-x_r)|.
| |
| \endaligned</math></center>
| |
| | |
| Z drugiej strony zauważmy, że dla wielomianu
| |
| <math>\displaystyle v(x)=Mx^{r+1}//(r+1)!</math> mamy <math>\displaystyle v\in F^r_M([a,b])</math> oraz
| |
| | |
| <center><math>\displaystyle \|v-w_v\|_{ C([a,b])}\,=\,\frac M{(r+1)!}\cdot
| |
| \max_{a\le x\le b}|(x-x_0)\cdots(x-x_r)|,
| |
| </math></center>
| |
| | |
| co kończy dowód.}}
| |
| | |
| [[Image:MNXXX.png|thumb|400px||Zjawisko Rungego]]
| |
| | |
| Zauważmy, że błąd aproksymacji
| |
| <math>\displaystyle e(F^r_M([a,b]);x_0,\ldots,x_r)</math> w istotny sposób
| |
| zależy od wyboru węzłów <math>\displaystyle x_j</math>. Naturalne jest więc
| |
| teraz następujące pytanie. W których punktach <math>\displaystyle x_j</math>
| |
| przedziału <math>\displaystyle [a,b]</math> należy obliczać wartości funkcji,
| |
| aby błąd był minimalny? Problem ten sprowadza się
| |
| oczywiście do minimalizacji wielkości
| |
| <math>\displaystyle \max_{a\le x\le b}|(x-x_0)\cdots(x-x_r)|</math>
| |
| względem węzłów <math>\displaystyle x_j</math>.
| |
| | |
| {{twierdzenie|O "optymalnym" doborze węzłów||
| |
| | | |
| Błąd aproksymacji w klasie funkcji <math>\displaystyle F^r_M([a,b])(x_0,\cdots,x_r)</math>
| | </div></div> |
| jest minimalny gdy węzły
| |
|
| |
|
| <center><math>\displaystyle x_j^*\,=\,\frac{b-a}2\cdot
| | ==Numeryczna poprawność eliminacji Gaussa== |
| \cos\left(\frac{2j+1}{2r+2}\pi\right)\,+\,
| |
| \frac{a+b}2,\qquad 0\le j\le r.
| |
| </math></center>
| |
|
| |
|
| Ponadto, dla węzłów optymalnych <math>\displaystyle x_j^*</math> mamy
| | Przedstawimy bez dowodu klasyczne twierdzenie o "praktycznej numerycznej |
| | poprawności" eliminacji Gaussa z wyborem w kolumnie. |
|
| |
|
| <center><math>\displaystyle e(F_M^r([a,b]);x_0^*,\ldots,x_r^*)\,=\,
| | {{twierdzenie|Wilkinsona|Wilkinsona| |
| \frac{2M}{(r+1)!}\left(\frac{b-a}4\right)^{r+1}.
| |
| </math></center>
| |
| | |
| }}
| |
|
| |
|
| Dowód tego twierdzenia opiera się na własnościach
| | Algorytm eliminacji Gaussa z wyborem elementu głównego w kolumnie, zrealizowany |
| pewnego ważnego ciągu wielomianów, który teraz
| | w arytmetyce <math>fl_\nu</math>, |
| przedstawimy.
| |
|
| |
|
| ====Wielomiany Czebyszewa====
| | wyznacza <math>\widetilde{x}</math> taki, że <math>\widetilde{x}</math> jest <strong>dokładnym</strong> rozwiązaniem zadania zaburzonego |
|
| |
|
| Ciąg <math>\displaystyle \{T_k\}_{k\ge 0}</math> ''wielomianów Czebyszewa''
| | <center><math>\widetilde{A}\widetilde{x} = b</math>,</center> |
| (pierwszego rodzaju) zdefiniowany jest indukcyjnie jako
| |
|
| |
|
| <center><math>\displaystyle \aligned T_0(x) &= 1, \\
| | przy czym |
| T_1(x) &= x, \\
| |
| T_{k+1}(x) &= 2xT_k(x)-T_{k-1}(x),\qquad
| |
| \mbox{ dla } \quad k\ge 1.
| |
| \endaligned</math></center>
| |
|
| |
|
| Zauważmy, że <math>\displaystyle T_k</math> jest wielomianem stopnia dokładnie
| | <center><math>\frac{||A-\widetilde{A}||_\infty}{||A||_\infty} \leq K \, N^3 \, \rho_N \, \nu</math>,</center> |
| <math>\displaystyle k</math> o współczynniku przy <math>\displaystyle x^k</math> równym <math>\displaystyle 2^{k-1}</math> | |
| (<math>\displaystyle k\ge 1</math>). Ponadto wielomian <math>\displaystyle T_k</math> można dla <math>\displaystyle |x|\le 1</math>
| |
| przedstawić w postaci
| |
|
| |
|
| <center><math>\displaystyle | | dla pewnej niedużej stałej <math>K = O(1)</math>. <strong>Wskaźnik wzrostu</strong> <math>\rho_N</math> definiujemy tutaj jako |
| T_k(x)\,=\,\cos(k\arccos x).
| | <center><math>\rho_N = \frac{\max_{i,j}|\widetilde{u}_{ij}|}{\max_{i,j} |a_{ij}|}</math>,</center> |
| </math></center> | |
|
| |
|
| Rzeczywiście, łatwo sprawdzić, że jest to prawdą dla
| |
| <math>\displaystyle k=0,1</math>. Stosując podstawienie <math>\displaystyle \cos t=x</math>, <math>\displaystyle 0\le t\le\pi</math>,
| |
| oraz wzór na sumę cosinusów otrzymujemy dla <math>\displaystyle k\ge 1</math>
| |
|
| |
| <center><math>\displaystyle \cos((k+1)t)\,=\,2\cdot\cos t\cos(kt)\,-\,\cos((k-1)t),
| |
| </math></center>
| |
|
| |
| co jest równoważne formule rekurencyjnej dla <math>\displaystyle T_{k+1}</math>.
| |
|
| |
| Ze wzoru <math>\displaystyle T_k(x) = \cos(k\arccos x)</math> wynikają również inne ważne
| |
| własności wielomianów Czebyszewa. Norma wielomianu
| |
| Czebyszewa na <math>\displaystyle [-1,1]</math> wynosi
| |
|
| |
| <center><math>\displaystyle \|T_k\|_{ C([-1,1])}\,=\,\max_{-1\le x\le 1} |T_k(x)|
| |
| \,=\,1
| |
| </math></center>
| |
|
| |
| i jest osiągana w <math>\displaystyle k+1</math> punktach tego przedziału równych
| |
|
| |
| <center><math>\displaystyle
| |
| y_j\,=\,\cos\Big(\frac jk\pi\Big),\qquad 0\le j\le k,
| |
| </math></center>
| |
|
| |
| przy czym <math>\displaystyle T_k(y_j)=(-1)^j</math>.
| |
|
| |
| W końcu, <math>\displaystyle k</math>-ty wielomian Czebyszewa <math>\displaystyle T_k</math> ma dokładnie
| |
| <math>\displaystyle k</math> pojedynczych zer w <math>\displaystyle [-1,1]</math> równych
| |
|
| |
| <center><math>\displaystyle z_j\,=\,\cos\Big(\frac{2j+1}{2r}\pi\Big),
| |
| \qquad 0\le j\le k-1.
| |
| </math></center>
| |
|
| |
| Konsekwencją wymienionych własności jest następująca własność ekstremalna
| |
| wielomianów Czebyszewa.
| |
|
| |
| Przez <math>\displaystyle \overline{\Pi}_k</math> oznaczymy klasę wielomianów
| |
| stopnia <math>\displaystyle k</math> o współczynniku wiodącym równym <math>\displaystyle 1</math>, tzn.
| |
|
| |
| <center><math>\displaystyle \overline{\Pi}_k\,=\,\{\,w\in\Pi_k:\,
| |
| w(x)=x^k+\cdots\,\}.
| |
| </math></center>
| |
|
| |
| {{twierdzenie|o minimaksie||
| |
|
| |
| Niech <math>\displaystyle k\ge 1</math>. W klasie
| |
| <math>\displaystyle \overline{\Pi}_k</math> minimalną normę jednostajną na
| |
| przedziale <math>\displaystyle [-1,1]</math> ma wielomian <math>\displaystyle w^*=2^{1-k}T_k</math>, tzn.
| |
|
| |
| <center><math>\displaystyle \min_{w\in\overline{\Pi}_k}\|w\|_{C([-1,1])}\,=\,
| |
| \|w^*\|_{C([-1,1])}\,=\,\frac 1{2^{k-1}}.
| |
| </math></center>
| |
|
| |
|
| | gdzie <math>\widetilde{L}</math> i <math>\widetilde{U}</math> są numerycznie wyznaczonymi czynnikami rozkładu PA<math>=</math>LU. |
| }} | | }} |
|
| |
|
| <!--
| | Jak widzimy, kluczowe dla numerycznej poprawności jest oszacowanie ''wskaźnika wzrostu'' <math>\rho_N</math>. Okazuje się, co wiedział już Wilkinson, że |
| | | * w ogólnym przypadku, zachodzi oszacowanie <math>\rho_N \leq 2^{N-1}</math>, które jest osiągane dla macierzy |
| {{dowod|||
| |
| Zauważmy najpierw, że
| |
| <math>\displaystyle w^*\in\overline\Pi_k</math> oraz <math>\displaystyle \|w^*\|_{C([-1,1])}=2^{1-k}</math>.
| |
| Wystarczy więc pokazać, że norma każdego wielomianu
| |
| z <math>\displaystyle \overline\Pi_k</math> jest nie mniejsza niż <math>\displaystyle 2^{1-k}</math>.
| |
| | |
| Załóżmy, że jest przeciwnie, tzn. istnieje wielomian
| |
| <math>\displaystyle w\in\overline\Pi_k</math> taki, że
| |
| | |
| <center><math>\displaystyle \|w\|_{C([-1,1])}\,<\,\frac 1{2^{k-1}}\,=\,
| |
| \|w^*\|_{C([-1,1])}.
| |
| </math></center> | |
| | |
| Rozpatrzmy funkcję <math>\displaystyle \psi=w^*-w</math>. Ponieważ dla punktów
| |
| "maksymalnych" zdefiniowanych w ([[##maxmm|Uzupelnic: maxmm ]]) mamy
| |
| <math>\displaystyle w^*(y_{k-j})=(-1)^j2^{1-k}</math> oraz <math>\displaystyle |w(y_{k-j})|<2^{1-k}</math>,
| |
| to
| |
|
| |
|
| <center><math>\displaystyle \psi(y_{k-j})\,\left\{\,\begin{array} {ll} | | <center><math>W = \begin{pmatrix} |
| > 0 &\quad j\mbox{-parzyste}, \\
| | 1 & & & 1 \\ |
| < 0 &\quad j\mbox{-nieparzyste}.
| | -1 & \ddots & & \vdots\\ |
| \end{array} \right.
| | \vdots & & \ddots & \vdots\\ |
| | -1 & \cdots & -1 & 1\\ |
| | \end{pmatrix} ; |
| </math></center> | | </math></center> |
| | | * dla macierzy trójdiagonalnych lub diagonalnie dominujących, lub dla macierzy symetrycznych dodatnio określonych, <math>\rho_N \leq 2</math>; |
| <math>\displaystyle 0\le j\le k</math>.
| | * w średnim przypadku, obserwuje się <math>\rho_N \leq N^{2/3}</math>, to znaczy macierze spotykane w praktyce obliczeniowej mają mały wskaźnik wzrostu. |
| Stąd <math>\displaystyle \psi</math> ma co najmniej jedno zero w każdym z
| |
| przedziałów <math>\displaystyle (y_i,y_{i+1})</math> dla <math>\displaystyle 0\le i\le k-1</math>, czyli
| |
| w sumie <math>\displaystyle k</math> zer. Z drugiej strony, <math>\displaystyle \psi</math> jest wielomianem | |
| stopnia co najwyżej <math>\displaystyle k-1</math> (bo współczynniki przy <math>\displaystyle x^k</math>
| |
| w wielomianach <math>\displaystyle w^*</math> i <math>\displaystyle w</math> redukują się), a więc
| |
| <math>\displaystyle \psi=0</math> i <math>\displaystyle w^*=w</math>.
| |
| }}
| |
| | |
| -->
| |
|
| |
| {{dowod|Twierdzenia o optymalnym doborze węzłów||
| |
| | | |
| Dowód wynika teraz
| | Konkluzja jest więc taka, że <strong>algorytm eliminacji Gaussa z wyborem w kolumnie |
| bezpośrednio z twierdzenia o minimaksie. Zauważmy bowiem, że
| | jest ''praktycznie'' numerycznie poprawny</strong>. Z drugiej strony, dla bardzo dużych |
| wielomian <math>\displaystyle (x-x_0)(x-x_1)\cdots(x-x_r)</math> jest w klasie
| | <math>N</math> i niezbyt dobrze uwarunkowanych macierzy, może okazać się, że arytmetyka |
| <math>\displaystyle \overline\Pi_{r+1}</math>. Stąd dla <math>\displaystyle [a,b]=[-1,1]</math> optymalnymi
| | pojedynczej precyzji może okazać się niewystarczająca dla uzyskania godnego |
| węzłami są zera <math>\displaystyle z_j</math> wielomianu Czebyszewa, przy których
| | wyniku. |
| | |
| <center><math>\displaystyle (x-z_0)(x-z_1)\cdots(x-z_r)\,=\,\frac{T_{r+1}(x)}{2^r}.
| |
| </math></center>
| |
| | |
| Jeśli przedział <math>\displaystyle [a,b]</math> jest inny niż <math>\displaystyle [-1,1]</math>, należy
| |
| dokonać liniowej zamiany zmiennych tak, aby przeszedł on na
| |
| <math>\displaystyle [-1,1]</math>. Bezpośrednie sprawdzenie pokazuje, że w klasie
| |
| <math>\displaystyle \overline\Pi_{r+1}</math> minimalną normę Czebyszewa na
| |
| przedziale <math>\displaystyle [a,b]</math> ma wielomian
| |
|
| |
|
| <center><math>\displaystyle w_{a,b}^*(x)\,=\,\Big(\frac{b-a}{2}\Big)^{r+1}
| | Algorytm eliminacji Gaussa z pełnym wyborem elementu głównego jest |
| w^*\left(\frac{2x-(a+b)}{b-a}\right).
| | numerycznie poprawny, ze wskaźnikiem wzrostu <math>\rho_N \leq \sqrt{n\cdot 2 \cdot |
| </math></center> | | 3^{1/2}\cdot 4^{1/3}\cdots N^{1/(N-1)}}</math>, a w praktyce grubo poniżej <math>\sqrt{N}</math>. |
|
| |
|
| Stąd
| | ==Literatura== |
|
| |
|
| <center><math>\displaystyle \|w_{a,b}^*\|_{C([a,b])}\,=\,\Big(\frac{b-a}{2}\Big)^{r+1} | | W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj <b>rozdział 4.4 i, nieobowiązkowo, 4.5</b> w |
| \frac 1{2^r}\,=\,2\,\Big(\frac{b-a}{4}\Big)^{r+1}
| | * D. Kincaid, W. Cheney <cite>Analiza numeryczna</cite>, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X. |
| </math></center> | |
|
| |
|
| i węzły <math>\displaystyle x^*_j</math> są optymalne.}}
| | Bardzo dużo informacji na temat omawianych zagadnień znajduje się w monografiach |
| | * <span style="font-variant:small-caps">A.Kiełbasiński, H. Schwetlick</span>, <cite>Numeryczna algebra liniowa</cite>, Wydawnictwa Naukowo-Techniczne, Warszawa, 1992, |
| | * <span style="font-variant:small-caps">N. Higham</span>, <cite>Accuracy and Stability of Numerical Algorithms</cite>, SIAM, 2002. |