TC Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 2 wersji utworzonych przez jednego użytkownika) | |||
| Linia 61: | Linia 61: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd7.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd7.png]] | ||
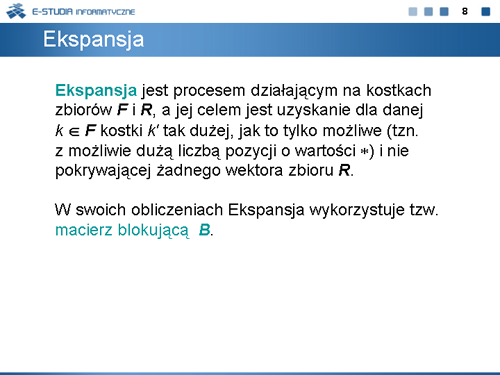
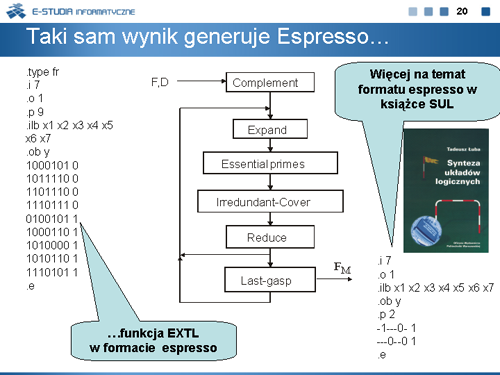
|valign="top"|Na planszy przedstawiono tablicę prawdy funkcji boolowskiej 7-argumentowej oraz podano odpowiednie zbiory <math>F\,</math> i <math>R\,</math> tej funkcji. Funkcję tę w dalszej części wykładu oznaczać będziemy EXTL. Wektory zbioru <math>F\,</math> oznaczono symbolami <math>k_1, | |valign="top"|Na planszy przedstawiono tablicę prawdy funkcji boolowskiej 7-argumentowej oraz podano odpowiednie zbiory <math>F\,</math> i <math>R\,</math> tej funkcji. Funkcję tę w dalszej części wykładu oznaczać będziemy EXTL. Wektory zbioru <math>F\,</math> oznaczono symbolami <math>k_1,\ldots,k_5\,</math> . | ||
|} | |} | ||
| Linia 103: | Linia 103: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd11.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd11.png]] | ||
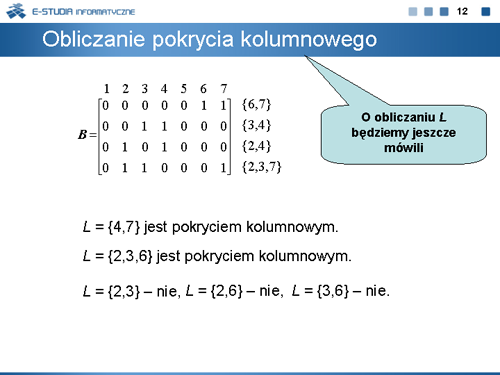
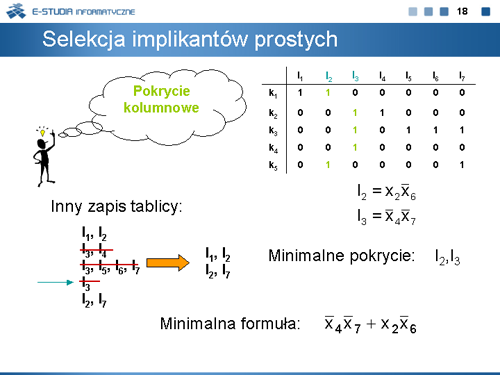
|valign="top"|Pokryciem kolumnowym macierzy <math>B=[b_{ij}]</math>, <math>i\epsilon \left \{1, | |valign="top"|Pokryciem kolumnowym macierzy <math>B=[b_{ij}]</math>, <math>i\epsilon \left \{1,\ldots,w\right \}\,</math>, <math>j\epsilon \left \{1,\ldots,n\right \}\,</math> jest zbiór <math>L\subseteq \left \{1,\ldots,n\right \}\,</math> taki, że dla każdego <math>i\epsilon \left \{1,\ldots,w\right \}\,</math> istnieje <math>j\epsilon L\,</math> , dla którego <math>b_{ij} = 1</math> . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje <math>L' \subseteq L\,</math>, który jest pokryciem macierzy <math>B\,</math>. | ||
|} | |} | ||
| Linia 147: | Linia 147: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd15.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd15.png]] | ||
|valign="top"| | |valign="top"|Postępując podobnie dla pozostałych kostek uzyskujemy następujące zbiory implikantów prostych funkcji <math>F\,</math>: | ||
<math>\begin{matrix} I_1=\overline{x}_1 & I_3=\overline{x}_4\overline{x}_7 & I_5=\overline{x}_5 & I_7=x_3\overline{x}_6 \\ I_2=x_2\overline{x}_6 & I_4=\overline{x}_2\overline{x}_3x_6 & I_6=\overline{x}_6\overline{x}_7 \end{matrix}</math> | |||
Spośród obliczonych implikantów prostych należy teraz wyselekcjonować minimalny podzbiór implikantów pokrywający wszystkie wektory prawdziwe realizowanej funkcji. Proces selekcji wykonuje się za pośrednictwem tzw. tablicy implikantów prostych. | |||
|} | |} | ||
| Linia 154: | Linia 160: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd16.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd16.png]] | ||
|valign="top"| | |valign="top"|W celu utworzenia tablicy implikantów prostych skorzystamy z relacji pokrycia dla kostek: | ||
<math>k \subseteq k'\,</math> wtedy i tylko wtedy, gdy <math>k_i= {k'}_i\,</math> lub <math>{k'}_i=*</math> dla każdego <math>i\,</math> , <math>1\le i\le n\,</math> , | |||
gdzie: <math>k=(k_1,\ldots,k_n)</math> i <math>k'=({k'}_1,\ldots,{k'}_n)</math> . | |||
Na tej podstawie dla każdego obliczonego w poprzednim etapie implikanta (ale interpretowanego jako kostka) wyznaczamy wszystkie kostki zbioru <math>F\,</math> pokrywane przez ten implikant. Przykładowo | |||
:<math>I_1=\overline{x}_1\supseteq k_1</math> | |||
:<math>I_2=x_2\overline{x}_6\supseteq k_1,\, k_5</math> | |||
:<math>I_3=\overline{x}_4\overline{x}_7\supseteq k_2,\, k_3,\, k_4\,</math> | |||
|} | |} | ||
Aktualna wersja na dzień 21:58, 15 wrz 2023

|
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
Pokryciem kolumnowym macierzy , , jest zbiór taki, że dla każdego istnieje , dla którego . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje , który jest pokryciem macierzy . |