TC Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 11 wersji utworzonych przez jednego użytkownika) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd1.png]] | |||
|valign="top"|Minimalizacja funkcji boolowskich metodą ekspansji. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd2.png]] | |||
|valign="top"|Kolejną klasyczną metodą minimalizacji funkcji boolowskich jest metoda Quine’a-McCluskey’a . Jest ona wykonywana w dwóch etapach: | |||
a) generacji implikantów prostych, | |||
b) selekcji minimalnego zbioru implikantów wiernie reprezentującego funkcję <math>f\,</math>. | |||
Mimo dużej złożoności obliczeniowej każdego z wyżej wymienionych etapów, metoda Quine’a-McCluskey’a jest najczęściej nauczaną metodą minimalizacji, głównie ze względu na podstawowy charakter jej procedur. Niestety – podobnie jak w przypadku tablic Karnaugha – jest to metoda absolutnie nieprzydatna do algorytmicznych obliczeń komputerowych. Dla potrzeb komputerowych systemów projektowania układów cyfrowych opracowano wiele nowych metod minimalizacji funkcji boolowskich. Najbardziej znaną i uznawaną za najskuteczniejszą jest metoda ESPRESSO opracowana w latach 80. na Uniwersytecie Kalifornijskim w Berkeley. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd3.png]] | |||
|valign="top"|Metoda Espresso polega na iteracyjnym stosowaniu różnych procedur, z których najważniejsze to Ekspansja (Expand), Pokrycie nienadmiarowe (''Irredundant Cover'') i Uzupełnienie (''Complement''). Są to bardzo złożone procedury, których omówienie przekracza zakres niniejszego wykładu. Ich pełny opis można znaleźć w książce Brayton R., Hachtel G.D., McMullen C., and Sangiovanni-Vincentelli A.: ''Logic Minimization Algorithms for VLSI Synthesis''. Kluwer Academic Publishers, Boston, 1984 lub w podręczniku ''Synteza układów logicznych''. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd4.png]] | |||
|valign="top"|Najprostszą i najogól¬niejszą procedurą metody ESPRESSO jest procedura Ekspansji. Sama procedura ekspansji wykorzystuje znaną od dawna metodę powiększania mintermu <math>k \epsilon F\,</math> w taki sposób, aby powiększona kostka nie zawierała żadnego mintermu należącego do zbioru wektorów zerowych funkcji. Ponieważ właściwie powiększony minterm zbioru <math>F\,</math> może być implikantem funkcji, odpowiednio zmodyfikowana metoda ekspansji może być stosowana autonomicznie jako niezależna metoda minimalizacji funkcji boolowskich. Metoda ta została zrealizowana w programie PANDOR. Program ten jest udostępniony na stronie internetowej www.zpt.tele.pw.edu.pl w katalogu OPROGRAMOWANIE. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd5.png]] | |||
|valign="top"|Pojęciem podstawowym w metodzie ekspansji jest – podobnie jak w innych metodach minimalizacji – pojęcie kostki. Kostkami nazywać będziemy ciągi elementów ze zbioru <math>\left \{0, 1, *\right \}</math> . Kostki będziemy oznaczać nieindeksowanymi literami, na przykład <math>k\,</math> , a ich składowe będziemy indeksowali, na przykład <math>k_i\,</math> . Również, w celu uproszczenia oznaczeń kostki (i wektory) będziemy zapisywać bez przecinków. Na przykład <math>(*,1,*,0,1)\,</math> zapiszemy jako <math>(*1*01)\,</math>. | |||
Kostka to uproszczony zapis zbioru wektorów binarnych. Kostka <math>K=(0*1*)</math> reprezentuje zbiór wektorów: | |||
:<math>\begin{matrix} 0010 \\ 0011 \\ 0110 \\ 0111 \end{matrix}</math> | |||
Kostka reprezentuje również niepełny iloczyn zmiennych binarnych: Na przykład kostkę <math>K=0*1*</math> można zapisać jako <math>\overline{x}_1x_3\,</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd6.png]] | |||
|valign="top"|W metodzie ekspansji podobnie jak w standardzie Espresso zbiór wektorów (w ogólności kostek), dla których funkcja <math>f=1\,</math> oznacza się <math>F\,</math>. Natomiast zbiór tych wektorów (kostek), dla których funkcja <math>f=0\,</math> oznacza się <math>R\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd7.png]] | |||
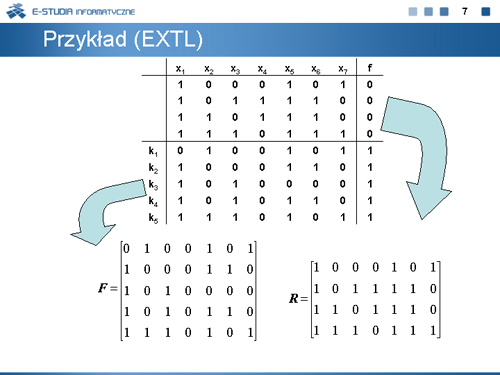
|valign="top"|Na planszy przedstawiono tablicę prawdy funkcji boolowskiej 7-argumentowej oraz podano odpowiednie zbiory <math>F\,</math> i <math>R\,</math> tej funkcji. Funkcję tę w dalszej części wykładu oznaczać będziemy EXTL. Wektory zbioru <math>F\,</math> oznaczono symbolami <math>k_1,\ldots,k_5\,</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd8.png]] | |||
|valign="top"|Ekspansja jest procesem działającym na kostkach zbiorów <math>F\,</math> i <math>R\,</math>, a jej celem jest uzyskanie dla danej <math>k \epsilon F\,</math> kostki <math>k'\,</math> tak dużej, jak to tylko możliwe (tzn. z możliwie dużą liczbą pozycji o wartości <math>*\,</math>) i nie pokrywającej żadnego wektora zbioru <math>R\,</math>. W swoich obliczeniach Ekspansja wykorzystuje tzw. macierz blokującą <math>B\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd9.png]] | |||
|valign="top"|Macierzą blokującą (kostkę k) nazywać będziemy macierz: | |||
<math>B(k,R)=[b_{ij}]</math> , <math>1\le i\le |R|\,</math> , <math>1\le j\le n\,</math> | |||
w której każdy element <math>b_{ij}\epsilon \left \{0,1\right \}</math> jest definiowany następująco: | |||
<math>b_{ij}=1</math> , jeśli <math>k_j=1</math> oraz <math>r_{ij}=0</math> lub <math>k_j=0</math> oraz <math>r_{ij}=1</math> ; | |||
<math>b_{ij}=0</math>, w pozostałych przypadkach. | |||
W przypadku funkcji opisanej wektorami binarnymi macierz blokująca dla danej kostki <math>k \epsilon F\,</math> powstaje z macierzy <math>R\,</math> przez zanegowanie tych kolumn <math>R\,</math>, których pozycje są wyznaczone przez pozycje jedynek w kostce <math>k \epsilon F\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd10.png]] | |||
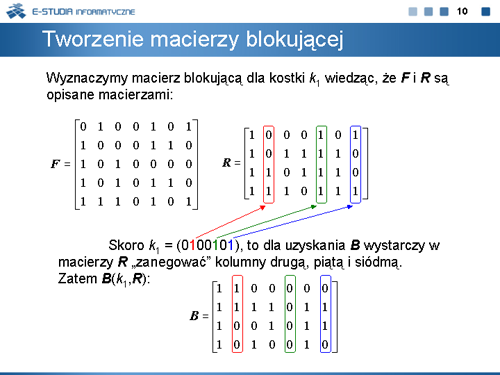
|valign="top"|Wyznaczymy macierz blokującą dla kostki <math>k_1\,</math> funkcji EXTL z planszy 7. Macierze <math>F\,</math> i <math>R\,</math> tej funkcji podane są ponownie na niniejszej planszy. Zgodnie z definicją, skoro <math>k_1=(0100101)</math>, to dla uzyskania <math>B\,</math> wystarczy w macierzy <math>R\,</math> „zanegować” kolumny drugą, piątą i siódmą, co zaznaczono odpowiednimi kolorami. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd11.png]] | |||
|valign="top"|Pokryciem kolumnowym macierzy <math>B=[b_{ij}]</math>, <math>i\epsilon \left \{1,\ldots,w\right \}\,</math>, <math>j\epsilon \left \{1,\ldots,n\right \}\,</math> jest zbiór <math>L\subseteq \left \{1,\ldots,n\right \}\,</math> taki, że dla każdego <math>i\epsilon \left \{1,\ldots,w\right \}\,</math> istnieje <math>j\epsilon L\,</math> , dla którego <math>b_{ij} = 1</math> . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje <math>L' \subseteq L\,</math>, który jest pokryciem macierzy <math>B\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd12.png]] | |||
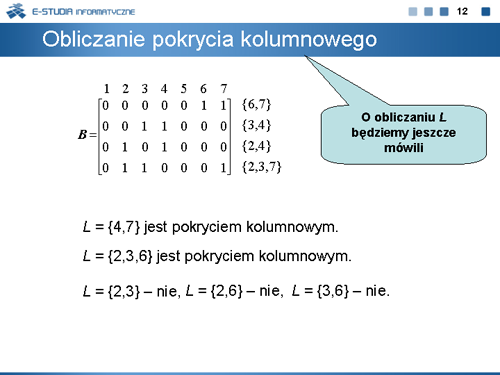
|valign="top"|Obliczenia pokrycia kolumnowego omówimy na przykładzie macierzy blokującej wyznaczonej dla kostki <math>k_2\,</math>. Dla tak obliczonej macierzy <math>B\,</math> , <math>L= \left \{2,3,6\right \}\,</math> (kolumny macierzy B są numerowane od lewej do prawej) jest minimalnym pokryciem kolumnowym. Natomiast <math>L= \left \{2, 3\right \}\,</math> , <math>L= \left \{2,6\right \}\,</math> oraz <math>L= \left \{3,6\right \}\,</math> nie są pokryciami kolumnowymi tej macierzy. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd13.png]] | |||
|valign="top"|Macierz blokująca <math>B(k,R)\,</math> pozwala wyznaczyć rozwinięcie (ekspansję) kostki <math>k\,</math> oznaczane <math>k^{+}(L,k)\,</math> w sposób następujący: | |||
<math>k^{+}_j = \begin{cases}k_j & ,gdy\, j\,\epsilon\, L \\ * & ,w\, pozostalych\, przypadkach \end{cases}</math> | |||
Można wykazać, że <math>k^{+}(L,k)\,</math> jest implikantem funkcji <math>f=(F,R)\,</math>. W szczególności <math>k^{+}(L,k)\,</math> jest implikantem prostym, gdy <math>L\,</math> jest minimalnym pokryciem kolumnowym macierzy <math>B(k,R)\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd14.png]] | |||
|valign="top"|Kontynuujemy obliczenia dla funkcji EXTL. Dla kostki <math>k_2=(1000110)</math> odpowiednia macierz blokująca <math>B=B(k_2, R)</math> jest: | |||
::<math>\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7\\ \end{matrix}</math> | |||
<math>B=\,\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ | |||
0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 1 \end{bmatrix}</math> | |||
Zbiór <math>L= \left \{4,7\right \}\,</math> jest pokryciem kolumnowym B, a więc <math>k^{+}(L,k)=(***0**0)</math> , czyli implikantem <math>F\,</math> jest <math>\overline{x}_4\overline{x}_7\,</math> . Natomiast dla <math>L= \left \{2,3,6\right \}\,</math> (inne pokrycie kolumnowe), <math>k^{+}(L,k)=(*00**1*)=\overline{x}_2\overline{x}_3x_6</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
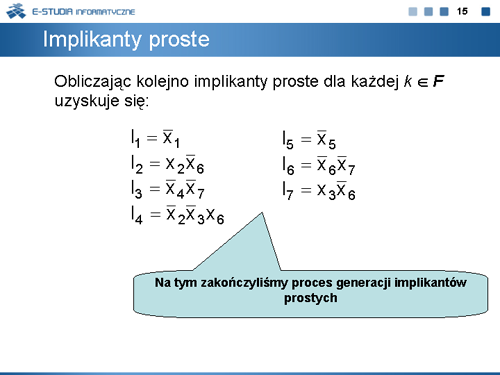
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd15.png]] | |||
|valign="top"|Postępując podobnie dla pozostałych kostek uzyskujemy następujące zbiory implikantów prostych funkcji <math>F\,</math>: | |||
<math>\begin{matrix} I_1=\overline{x}_1 & I_3=\overline{x}_4\overline{x}_7 & I_5=\overline{x}_5 & I_7=x_3\overline{x}_6 \\ I_2=x_2\overline{x}_6 & I_4=\overline{x}_2\overline{x}_3x_6 & I_6=\overline{x}_6\overline{x}_7 \end{matrix}</math> | |||
Spośród obliczonych implikantów prostych należy teraz wyselekcjonować minimalny podzbiór implikantów pokrywający wszystkie wektory prawdziwe realizowanej funkcji. Proces selekcji wykonuje się za pośrednictwem tzw. tablicy implikantów prostych. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd16.png]] | |||
|valign="top"|W celu utworzenia tablicy implikantów prostych skorzystamy z relacji pokrycia dla kostek: | |||
<math>k \subseteq k'\,</math> wtedy i tylko wtedy, gdy <math>k_i= {k'}_i\,</math> lub <math>{k'}_i=*</math> dla każdego <math>i\,</math> , <math>1\le i\le n\,</math> , | |||
gdzie: <math>k=(k_1,\ldots,k_n)</math> i <math>k'=({k'}_1,\ldots,{k'}_n)</math> . | |||
Na tej podstawie dla każdego obliczonego w poprzednim etapie implikanta (ale interpretowanego jako kostka) wyznaczamy wszystkie kostki zbioru <math>F\,</math> pokrywane przez ten implikant. Przykładowo | |||
:<math>I_1=\overline{x}_1\supseteq k_1</math> | |||
:<math>I_2=x_2\overline{x}_6\supseteq k_1,\, k_5</math> | |||
:<math>I_3=\overline{x}_4\overline{x}_7\supseteq k_2,\, k_3,\, k_4\,</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd17.png]] | |||
|valign="top"|Tablicę implikantów prostych konstruujemy w następujący sposób. Jeśli implikant <math>I_j\,</math> pokrywa kostkę <math>k_i\,</math> , to na przecięciu wiersza wiersza <math>k_i\,</math> z kolumną <math>I_j\,</math> piszemy 1, w przeciwnym przypadku piszemy 0. | |||
Tablica implikantów prostych umożliwia wybór (selekcję) takiego minimalnego zbioru implikantów, który pokrywa wszystkie kostki funkcji pierwotnej | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
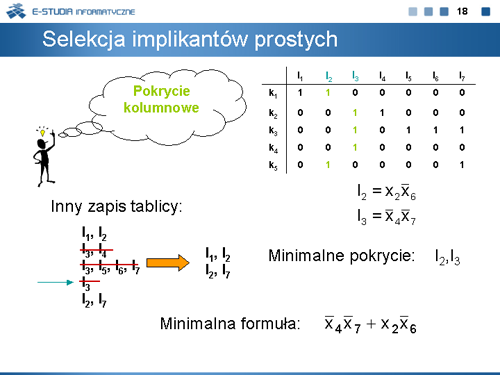
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd18.png]] | |||
|valign="top"|Minimalny zbiór implikantów prostych reprezentujących funkcję <math>f\,</math> można wyznaczyć obliczając minimalne pokrycie kolumnowe tablicy implikantów prostych. W tym celu zapisujemy wiersze tablicy w postaci zbiorów kolumn wskazywanych przez pozycje jedynek w danym wierszu, a następnie zauważając, że implikant <math>I_3\,</math> tworzy zbiór jednoelementowy wykreślamy wiersze z tym implikantem. Po takiej redukcji wierszy spostrzegamy, że I2 jest wspólny dla obu wierszy. Zatem minimalne pokrycie tworzą implikanty <math>I_2\,</math> , <math>I_3\,</math>. Czyli <math>f=\overline{x}_4\overline{x}_7+x_2\overline{x}_6</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
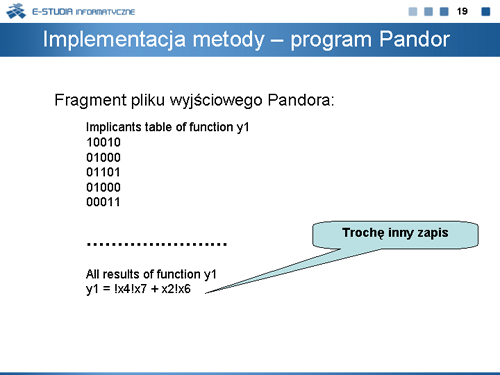
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd19.png]] | |||
|valign="top"|Analogiczny wynik obliczy program PANDOR. | |||
Pandor jest akademickim narzędziem minimalizacji funkcji boolowskich zmodyfikowaną metodą ekspansji z zastosowaniem dodatkowej procedury redukcji argumentów. Pandor został opracowany w ramach pracy dyplomowej Mirosława Cagary w Ośrodku Kształcenia na Odległość OKNO Politechniki Warszawskiej. Program Pandor jest dostępny na stronie internetowej www.zpt.tele.pw.edu.pl, a także na stronie internetowej jego autora www.domicil.pl. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd20.png]][[Grafika:TC_M4_Slajd21.png]] | |||
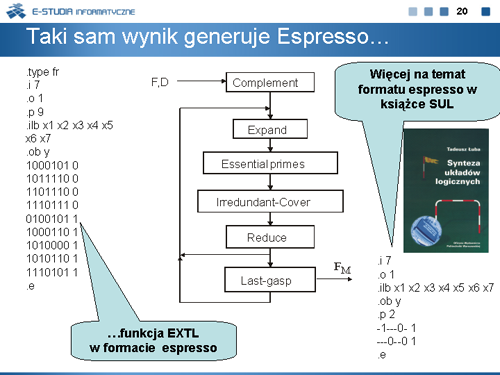
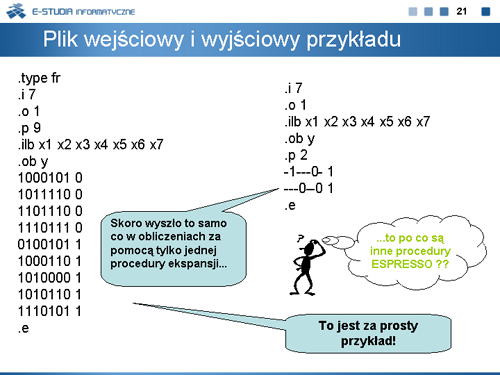
|valign="top"|Również program ESPRESSO obliczy taki sam wynik. Zapis funkcji EXTL w standardzie Espresso podano na planszach 20 i 21. Więcej informacji na temat standardu Espresso można znaleźć w książce ''Synteza układów logicznych''. | |||
Taki sam wynik minimalizacji funkcji EXTL w programie PANDOR (wyposażonym tylko w jedną procedurę ekspansji) oraz w programie ESPRESSO (zbudowanym z wielu procedur) nasuwa wątpliwości. Dlaczego program PANDOR za pomocą jednej procedury minimalizuje tak samo dobrze jak ESPRESSO zbudowane z wielu procedur. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd22.png]] | |||
|valign="top"|Barierą ograniczającą obliczenia systematyczną metodą zastosowaną w Pandorze jest ogromna złożoność obliczeniowa zarówno w procesie generacji, jak też w procesie obliczania pokrycia kolumnowego. | |||
Program PANDOR został stworzony po to, aby naocznie zaobserwować zjawisko wzrostu złożoności obliczeniowej wraz ze wzrostem liczby argumentów funkcji. | |||
Funkcja EXTL ma 7 implikantów (Pandor dokonuje lepszej selekcji i oblicza ich zaledwie 5). W tym przypadku obliczenie minimalnego pokrycia kolumnowego jest zadaniem łatwym. Ale już dla bardziej skomplikowanych funkcji takich jak TL27 i KAZ, których tablice w standardzie Espresso są podane na planszy, sytuacja jest całkiem inna – właśnie ze względu na dużą liczbę implikantów. Czas obliczeń programem PANDOR jest drastycznie większy od czasu obliczeń programem Espresso. Oczywiście Espresso nie zawsze poda wynik minimalny. W celu uzyskania minimalnych rozwiązań w rozsądnym czasie obliczeń w programie PANDOR zastosowano procedurę redukcji argumentów. Jej wpływ na proces minimalizacji omówimy w następnym wykładzie. | |||
|} | |||
<hr width="100%"> | |||
Aktualna wersja na dzień 21:58, 15 wrz 2023

|
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
Pokryciem kolumnowym macierzy , , jest zbiór taki, że dla każdego istnieje , dla którego . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje , który jest pokryciem macierzy . |