PS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 5 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd1.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Metody analizy sygnałów w dziedzinie częstotliwości noszą nazwę ''metod częstotliwościowych'' lub ''metod widmowych''. | *Metody analizy sygnałów w dziedzinie częstotliwości noszą nazwę ''metod częstotliwościowych'' lub ''metod widmowych''. | ||
*W „języku” częstotliwościowym można w wielu przypadkach w sposób prostszy opisać podstawowe cechy sygnału. Łatwiej jest też rozpatrywać i interpretować niektóre operacje na sygnałach, a zwłaszcza operację ''filtracji''. | *W „języku” częstotliwościowym można w wielu przypadkach w sposób prostszy opisać podstawowe cechy sygnału. Łatwiej jest też rozpatrywać i interpretować niektóre operacje na sygnałach, a zwłaszcza operację ''filtracji''. | ||
*Widmo <math>X(\omega)\ | *Widmo <math>X(\omega)\ </math>, sygnału <math>x(t)\ </math>, jest jego równoważną reprezentacją w dziedzinie częstotliwości. Ponieważ widmo jest w ogólnym przypadku funkcją zespoloną zmiennej rzeczywistej <math>\omega\ </math>, (por. przykład 3.1), reprezentacja ta ma charakter formalny, niefizyczny. | ||
|} | |} | ||
| Linia 11: | Linia 11: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd2.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd2.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Zwróćmy uwagę, że w przykładzie 3.2 otrzymaliśmy widmo rzeczywiste. Jest to konsekwencją parzystości sygnału <math>x(t)=X_0\Pi(t/T)</math> . Widmo to ma kształt funkcji Sa w dziedzinie częstotliwości. | *Zwróćmy uwagę, że w przykładzie 3.2 otrzymaliśmy widmo rzeczywiste. Jest to konsekwencją parzystości sygnału <math>x(t)=X_0\Pi(t/T)</math> . Widmo to ma kształt funkcji Sa w dziedzinie częstotliwości. | ||
*Dla sygnałów o ograniczonej energii (należących do przestrzeni <math>L^2(-\infty, \infty)\ | *Dla sygnałów o ograniczonej energii (należących do przestrzeni <math>L^2(-\infty, \infty)\ </math>, ) przekształcenie Fouriera jest wzajemnie jednoznaczne, jeśli całkę (3.1) rozumie się w sensie Lebesgue’a. | ||
*Wzory (3.1) i (3.2) określają proste i odwrotne przekształcenie Fouriera w sensie zwykłym. | *Wzory (3.1) i (3.2) określają proste i odwrotne przekształcenie Fouriera w sensie zwykłym. | ||
| Linia 22: | Linia 22: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd3.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd3.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Chcąc wyprowadzić parę transformat w sensie granicznym należy w każdym indywidualnym przypadku skonstruować odpowiedni ciąg sygnałów o ograniczonej energii aproksymujący sygnał o ograniczonej mocy i dokonać przejścia granicznego. Bardzo często w wyniku przejścia granicznego otrzymujemy w granicy widma dystrybucyjne. | *Chcąc wyprowadzić parę transformat w sensie granicznym należy w każdym indywidualnym przypadku skonstruować odpowiedni ciąg sygnałów o ograniczonej energii aproksymujący sygnał o ograniczonej mocy i dokonać przejścia granicznego. Bardzo często w wyniku przejścia granicznego otrzymujemy w granicy widma dystrybucyjne. | ||
*Ciąg aproksymujący sygnał <math>x(t)\ | *Ciąg aproksymujący sygnał <math>x(t)\ </math>, o ograniczonej mocy konstruuje się zwykle mnożąc go przez funkcje dążące dostatecznie szybko do zera dla <math>t\to \pm \infty\ </math>, typu: <math>e^{-\alpha t}1(t)\ </math>, , jeśli <math>t\epsilon[0, \infty)\ </math>, , oraz <math>e^{-\alpha |t|}\ </math> lub <math>e^{-\alpha t^2}\ </math> , jeśli <math>t\epsilon (-\infty, \infty)\ </math>, . | ||
|} | |} | ||
| Linia 31: | Linia 31: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe i widmo fazowe są funkcjami rzeczywistymi zmiennej <math>\omega\ | *Widmo amplitudowe i widmo fazowe są funkcjami rzeczywistymi zmiennej <math>\omega\ </math>, i mają wyraźną interpretację fizyczną. | ||
*Widma amplitudowe sygnału z przykładu 3.3 dąży do zera, gdy <math>\omega\to \pm \infty\ | *Widma amplitudowe sygnału z przykładu 3.3 dąży do zera, gdy <math>\omega\to \pm \infty\ </math>, . Jego gęstość widmowa jest skoncentrowana głównie w zakresie małych wartości pulsacji. Sygnały takie nazywamy ''dolnopasmowymi''. | ||
|} | |} | ||
| Linia 41: | Linia 41: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd5.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe impulsu prostokątnego z przykładu 3.4 ma charakterystyczną strukturę „listkową”. Środkowy przedział pulsacji <math>|\omega|<2\pi /T</math> obejmuje tzw. ''listek główny'', a po obu jego stronach występują ''listki boczne''. | *Widmo amplitudowe impulsu prostokątnego z przykładu 3.4 ma charakterystyczną strukturę „listkową”. Środkowy przedział pulsacji <math>|\omega|<2\pi /T</math> obejmuje tzw. ''listek główny'', a po obu jego stronach występują ''listki boczne''. | ||
| Linia 51: | Linia 51: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe sygnałów rzeczywistych jest funkcją parzystą, a widmo fazowe funkcją nieparzystą zmiennej <math>\omega\ | *Widmo amplitudowe sygnałów rzeczywistych jest funkcją parzystą, a widmo fazowe funkcją nieparzystą zmiennej <math>\omega\ </math>, . Widmo tych sygnałów jest zatem ''funkcją hermitowską'', tj. <math>X(\omega)=X^{*}(-\omega)</math> . | ||
*Operacje zwierciadlanego odbicia sygnału względem osi rzędnych i jego sprzężenia odpowiadają podobnym operacjom na jego widmie. | *Operacje zwierciadlanego odbicia sygnału względem osi rzędnych i jego sprzężenia odpowiadają podobnym operacjom na jego widmie. | ||
*Przekształcenie Fouriera jest liniowe, tzn. widmo kombinacji liniowej sygnałów jest taką samą kombinacją liniową ich widm. | *Przekształcenie Fouriera jest liniowe, tzn. widmo kombinacji liniowej sygnałów jest taką samą kombinacją liniową ich widm. | ||
*Przy przekształceniu Fouriera kształt sygnału i jego widma jest cechą wymienną. | *Przy przekształceniu Fouriera kształt sygnału i jego widma jest cechą wymienną. | ||
*Rozciągnięciu skali czasu sygnału odpowiada zawężenie skali częstotliwości jego widma i odwrotnie. Jednocześnie zmianie ulega skala wartości widma. | *Rozciągnięciu skali czasu sygnału odpowiada zawężenie skali częstotliwości jego widma i odwrotnie. Jednocześnie zmianie ulega skala wartości widma. | ||
*Przesunięciu sygnału wzdłuż osi czasu o czas <math>t_0\ | *Przesunięciu sygnału wzdłuż osi czasu o czas <math>t_0\ </math>, odpowiada mnożenie jego widma przez czynnik <math>e^{j\omega t_0}\ </math>, . Widmo amplitudowe nie zmienia się przy tym, a fazowe ulega zmianie o składnik <math>-\omega t_0\ </math>, . | ||
*Mnożenie sygnału przez zespolony sygnał harmoniczny o pulsacji <math>\omega_0\ | *Mnożenie sygnału przez zespolony sygnał harmoniczny o pulsacji <math>\omega_0\ </math>, powoduje przesunięcie jego widma wzdłuż osi pulsacji o wartość <math>\omega_0\ </math>, . | ||
*Mnożenie sygnału przez rzeczywisty sygnał harmoniczny o pulsacji <math>\omega_0\ | *Mnożenie sygnału przez rzeczywisty sygnał harmoniczny o pulsacji <math>\omega_0\ </math>, (jego modulacja) powoduje rozczepienie widma na dwie części przesunięte wzdłuż osi pulsacji do punktów <math>\pm \omega_0\ </math>, . Jednocześnie gęstość widmowa maleje dwukrotnie | ||
|} | |} | ||
| Linia 67: | Linia 67: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd7.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Różniczkowaniu sygnału w dziedzinie czasu odpowiada mnożenie jego widma przez <math>j\omega\ | *Różniczkowaniu sygnału w dziedzinie czasu odpowiada mnożenie jego widma przez <math>j\omega\ </math>, w dziedzinie częstotliwości. | ||
*Całkowaniu sygnału w dziedzinie czasu odpowiada dzielenie jego widma przez <math>j\omega\ | *Całkowaniu sygnału w dziedzinie czasu odpowiada dzielenie jego widma przez <math>j\omega\ </math>, w dziedzinie częstotliwości. | ||
*Splotowi sygnałów odpowiada mnożenie ich widm i odwrotnie, mnożeniu sygnałów odpowiada splatanie ich widm. | *Splotowi sygnałów odpowiada mnożenie ich widm i odwrotnie, mnożeniu sygnałów odpowiada splatanie ich widm. | ||
*Twierdzenie Rayleigha orzeka, że (z dokładnością do czynnika <math>2\pi\ | *Twierdzenie Rayleigha orzeka, że (z dokładnością do czynnika <math>2\pi\ </math>, ) w przestrzeniach sygnałów <math>{L^2}_t\ </math>, i widm <math>{L^2}_{\omega}\ </math>, jest zachowany iloczyn skalarny. Wynikające z niego twierdzenie Parsevala orzeka, że z dokładnością do czynnika <math>2\pi\ </math>, zachowana jest norma w obu przestrzeniach (lub równoważnie energia). | ||
*Widmo gęstości energii opisuje rozkład całkowitej energii sygnału wzdłuż osi pulsacji. | *Widmo gęstości energii opisuje rozkład całkowitej energii sygnału wzdłuż osi pulsacji. | ||
| Linia 80: | Linia 80: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd8.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Ponieważ sygnał wykładniczy obustronny jest parzysty jego widmo jest rzeczywiste i parzyste. Jak widać, jest to sygnał dolnopasmowy. Parę tę można bez trudu wyprowadzić wprost z definicji przekształcenia Fouriera. | *Ponieważ sygnał wykładniczy obustronny jest parzysty jego widmo jest rzeczywiste i parzyste. Jak widać, jest to sygnał dolnopasmowy. Parę tę można bez trudu wyprowadzić wprost z definicji przekształcenia Fouriera. | ||
*Obliczenie widma sygnału <math>Sa\ | *Obliczenie widma sygnału <math>Sa\ </math>, wprost z definicji jest bardzo złożone. Korzystając natomiast z twierdzenia o symetrii względem wcześniej wyprowadzonej pary transformat dla impulsu prostokątnego, widmo to można wyznaczyć bez trudu. Ponieważ widmo sygnału Sa jest prostokątne, sygnał ten nazywamy ''idealnym sygnałem dolnopasmowym''. | ||
*Widmo impulsu trójkątnego można wyznaczyć z twierdzenia o splocie w dziedzinie czasu przyjmując <math>x(t)=y(t)=\Pi(t/T)</math> . | *Widmo impulsu trójkątnego można wyznaczyć z twierdzenia o splocie w dziedzinie czasu przyjmując <math>x(t)=y(t)=\Pi(t/T)</math> . | ||
*Widmo sygnału <math>Sa^2\ | *Widmo sygnału <math>Sa^2\ </math>, wynika z twierdzenia o symetrii i ostatniej pary transformat. | ||
|} | |} | ||
| Linia 92: | Linia 92: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd9.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo sygnału Gaussa ma również kształt krzywej Gaussa. Jest to jedna z nielicznych par transformat Fouriera o tej właściwości | *Widmo sygnału Gaussa ma również kształt krzywej Gaussa. Jest to jedna z nielicznych par transformat Fouriera o tej właściwości | ||
| Linia 102: | Linia 102: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd10.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
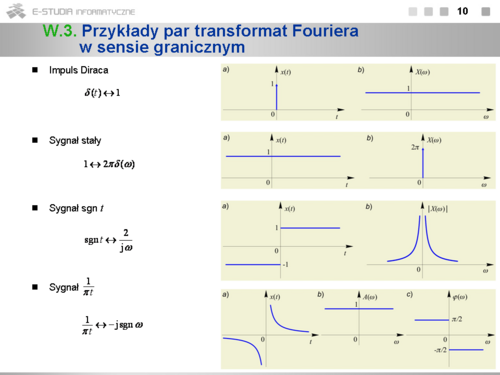
*Widmo impulsu Diraca jest stałe w całym przedziale pulsacji. Widmo takie nazywamy ''białym''. | *Widmo impulsu Diraca jest stałe w całym przedziale pulsacji. Widmo takie nazywamy ''białym''. | ||
*Widmo sygnału stałego jest dystrybucją Diraca w dziedzinie częstotliwości o polu <math>2\pi\ | *Widmo sygnału stałego jest dystrybucją Diraca w dziedzinie częstotliwości o polu <math>2\pi\ </math>, w punkcie <math>\omega=0\ </math>, . | ||
*Sygnał <math>sgn\, t\ | *Sygnał <math>sgn\, t\ </math>, jest nieparzysty, dlatego jego widmo jest urojone. | ||
*Para <math>1/{\pi} t\leftrightarrow -jsgn\, \omega</math> jest dualna względem pary <math>sgn\, t\leftrightarrow 2/j\omega</math> i wynika z twierdzenia o symetrii. | *Para <math>1/{\pi} t\leftrightarrow -jsgn\, \omega</math> jest dualna względem pary <math>sgn\, t\leftrightarrow 2/j\omega</math> i wynika z twierdzenia o symetrii. | ||
|} | |} | ||
| Linia 113: | Linia 113: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd11.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
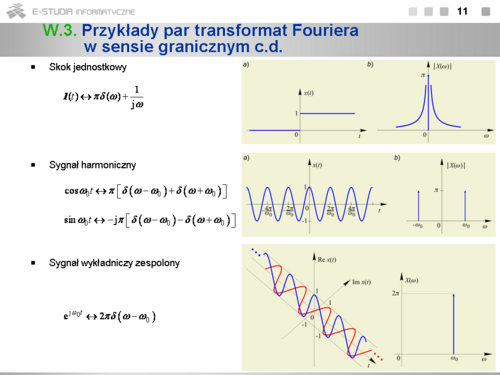
*Widmo skoku jednostkowego można wyznaczyć, przedstawiając go w postaci <math>1(t)=1/2+(sgn\, t)/2</math> i korzystając z poprzednio omówionych par. | *Widmo skoku jednostkowego można wyznaczyć, przedstawiając go w postaci <math>1(t)=1/2+(sgn\, t)/2</math> i korzystając z poprzednio omówionych par. | ||
*Widmo sygnału harmonicznego wynika z twierdzenia o modulacji zastosowanego do pary <math>1\leftrightarrow 2\pi \delta (\omega)</math> . Widmo to składa się z dwóch dystrybucji Diraca (prążków) występujących w punktach <math>\pm \omega_0\ | *Widmo sygnału harmonicznego wynika z twierdzenia o modulacji zastosowanego do pary <math>1\leftrightarrow 2\pi \delta (\omega)</math> . Widmo to składa się z dwóch dystrybucji Diraca (prążków) występujących w punktach <math>\pm \omega_0\ </math>, . | ||
*Widmo zespolonego sygnału harmonicznego o pulsacji <math>\omega_0\ | *Widmo zespolonego sygnału harmonicznego o pulsacji <math>\omega_0\ </math>, jest dystrybucją Diraca w punkcie <math>\omega_0\ </math>, o polu <math>2\pi\ </math>, . | ||
|} | |} | ||
| Linia 123: | Linia 123: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd12.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Ogólna postać widma sygnału okresowego o okresie <math>T_0=2\pi/{omega_0}</math> wynika z jego rozwinięcia w zespolony szereg Fouriera <math>x(t)=\sum_{k=-\infty}^{\infty} X_k e^{jk\omega_0 t}</math> , twierdzenia o liniowości oraz pary <math>e^{jk\omega_0 t}\leftrightarrow 2\pi \delta(\omega-k\omega_0) </math> . Widmo to jest ciągiem dystrybucji Diraca występujących w punktach <math>k\omega_0\ | *Ogólna postać widma sygnału okresowego o okresie <math>T_0=2\pi/{omega_0}</math> wynika z jego rozwinięcia w zespolony szereg Fouriera <math>x(t)=\sum_{k=-\infty}^{\infty} X_k e^{jk\omega_0 t}</math> , twierdzenia o liniowości oraz pary <math>e^{jk\omega_0 t}\leftrightarrow 2\pi \delta(\omega-k\omega_0)</math> . Widmo to jest ciągiem dystrybucji Diraca występujących w punktach <math>k\omega_0\ </math>, , <math>k=0,\pm\ 1,...\ </math>, , co oddaje jego dyskretny charakter. | ||
*Widmo amplitudowe jest ciągiem dystrybucji Diraca w punktach <math>k\omega_0\ | *Widmo amplitudowe jest ciągiem dystrybucji Diraca w punktach <math>k\omega_0\ </math>, i polach <math>2\pi |X_k|\ </math>, , zaś widmo fazowe jest ciągiem zwykłych liczb <math>X_k\ </math>, . | ||
*Widmo unipolarnej fali prostokątnej z przykładu 3.5 jest ciągiem dystrybucji Diraca, których obwiednią jest funkcja <math>Sa\ | *Widmo unipolarnej fali prostokątnej z przykładu 3.5 jest ciągiem dystrybucji Diraca, których obwiednią jest funkcja <math>Sa\ </math>,. | ||
|} | |} | ||
| Linia 134: | Linia 134: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd13.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd13.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo unipolarnej fali prostokątnej wykreślono dla dwóch różnych wartości okresu fali <math>T_0\ | *Widmo unipolarnej fali prostokątnej wykreślono dla dwóch różnych wartości okresu fali <math>T_0\ </math>, i stałej szerokości impulsu <math>T\ </math>, . W miarę zwiększania okresu prążki zagęszczają się i ich wysokości maleją. Nie zmieniają się natomiast miejsca zerowe obwiedni, które zależą tylko od szerokości impulsu <math>T\ </math>, . | ||
|} | |} | ||
| Linia 143: | Linia 143: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd14.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd14.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
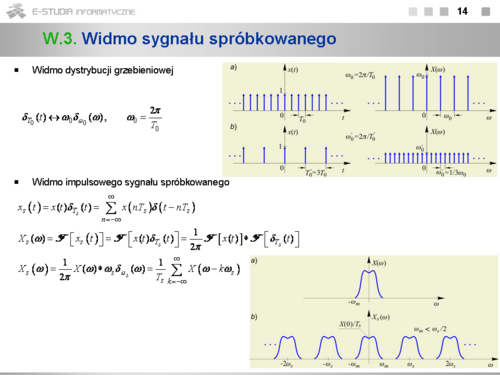
*Widmo w sensie granicznym dystrybucji grzebieniowej <math>\delta_{T_0}(t)</math> o okresie <math>T_0\ | *Widmo w sensie granicznym dystrybucji grzebieniowej <math>\delta_{T_0}(t)</math> o okresie <math>T_0\ </math>, jest również dystrybucją grzebieniową <math>\omega_0 \delta_{\omega_0}(\omega)\ </math>, o okresie <math>\omega_0=2\pi/T_0</math> i jednakowych polach impulsów widmowych równych <math>\omega_0\ </math>, . Wynika to z faktu, co można łatwo pokazać wykonując odpowiednie obliczenie, że współczynniki rozwinięcia dystrybucji <math>\delta_{T_0}(t)</math> w zespolony szereg Fouriera są identyczne dla każdego <math>k\ </math>, i równe <math>X_k=1/T_0</math> . | ||
*Widmo impulsowego sygnału spróbkowanego z okresem <math>T_s\ | *Widmo impulsowego sygnału spróbkowanego z okresem <math>T_s\ </math>, wyznaczamy na podstawie twierdzenia o splocie w dziedzinie częstotliwości i właściwości powielenia okresowego dystrybucji Diraca. Widmo to jest okresowym powieleniem z okresem <math>\omega_s\ </math>, widma <math>X(\omega)\ </math>, sygnału próbkowanego <math>x(t)\ </math>, . Jeśli sygnał <math>x(t)\ </math>, jest sygnałem o paśmie ograniczonym pulsacją <math>\omega_m\le \omega_s/2</math> , to widmo powielone jest ciągiem niezniekształconych kopii widma <math>X(\omega)\ </math>, skalowanych przez współczynnik <math>1/T_0\ </math>, . | ||
|} | |} | ||
| Linia 153: | Linia 153: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd15.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd15.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Szereg Fouriera można traktować jako szczególny przypadek przekształcenia Fouriera sygnałów okresowych w sensie granicznym. | |||
*Współczynniki rozwinięcia sygnału okresowego o okresie <math>T_0\ </math>, w zespolony szereg Fouriera są określone przez wartości widma centralnego segmentu tego sygnału w punktach <math>k\omega_0\ </math>, , <math>\omega_0=1\pi/T_0</math> , podzielone przez <math>T_0\ </math>, . | |||
|} | |} | ||
| Linia 161: | Linia 163: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd16.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd16.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*W teorii obwodów obowiązuje zasada, że im czas trwania sygnału jest krótszy (im impuls jest węższy), tym jego widmo jest szersze. | |||
:''Zasada nieoznaczoności'' w teorii sygnałów stanowi, że iloczyn miary czasu trwania sygnału i miary szerokości widma nie może być mniejszy od pewnego progu. | |||
*Zasada nieoznaczoności znajduje odbicie w wielu zastosowaniach praktycznych. Np. w projektowaniu cyfrowych systemów telekomunikacyjnych dąży się do przesyłania informacji za pomocą jak najkrótszych impulsów, co skraca czas transmisji, i jednocześnie do przesyłania informacji w jak najkrótszym paśmie, co zwiększa pojemność systemu. Zgodnie z zasadą nieoznaczoności wymagania te są sprzeczne i wyboru czasu trwania impulsu i szerokości jego widma dokonuje się na drodze kompromisu. | |||
|} | |} | ||
<hr width="100%" | <hr width="100%"> | ||