PEE Moduł 9: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 19 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd1.png|500px]] | ||
|valign="top"|'''Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów''' | |valign="top"|'''Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów''' | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd2.png|500px]] | ||
|valign="top"|Weźmy pod uwagę obwód złożony z dowolnych elementów pasywnych RLCM i źródeł sterowanych nie zawierających wewnątrz żadnych źródeł niezależnych. Wyróżnijmy w tym obwodzie jedną parę zacisków uważanych za wejściowe, do których przykładamy źródło wymuszające oraz drugą parę zacisków wyjściowych, z których zbieramy prąd (zaciski zwarte) lub napięcie (zaciski rozwarte). | |valign="top"|Weźmy pod uwagę obwód złożony z dowolnych elementów pasywnych <math>RLCM</math> i źródeł sterowanych nie zawierających wewnątrz żadnych źródeł niezależnych. Wyróżnijmy w tym obwodzie jedną parę zacisków uważanych za wejściowe, do których przykładamy źródło wymuszające oraz drugą parę zacisków wyjściowych, z których zbieramy prąd (zaciski zwarte) lub napięcie (zaciski rozwarte). | ||
Transmitancja operatorowa określa związek między transformatą operatorową sygnału wyjściowego (odpowiedzi), którą tutaj oznaczymy w ogólności przez Y(s) oraz transformatą operatorową wymuszenia (sygnału wejściowego), oznaczoną ogólnie przez X(s). Transmitancją operatorową nazywać będziemy stosunek transformaty sygnału wyjściowego (prądu lub napięcia) do transformaty sygnału wejściowego układu (źródła napięciowego lub prądowego) przy zerowych warunkach początkowych | Transmitancja operatorowa określa związek między transformatą operatorową sygnału wyjściowego (odpowiedzi), którą tutaj oznaczymy w ogólności przez <math>Y(s)</math> oraz transformatą operatorową wymuszenia (sygnału wejściowego), oznaczoną ogólnie przez <math>X(s)</math>. Transmitancją operatorową nazywać będziemy stosunek transformaty sygnału wyjściowego (prądu lub napięcia) do transformaty sygnału wejściowego układu (źródła napięciowego lub prądowego) przy zerowych warunkach początkowych | ||
: <math>T(s)=\frac{Y(s)}{X(s)}</math> | : <math>T(s)=\frac{Y(s)}{X(s)}</math> | ||
| Linia 22: | Linia 20: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd3.png|500px]] | ||
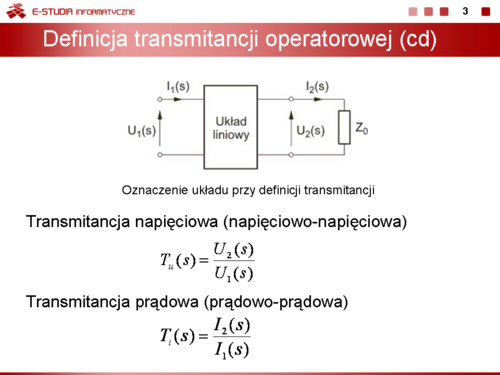
|valign="top"|Przyjmijmy oznaczenie bramy wejściowej cyfrą 1 a bramy wyjściowej cyfrą 2 jak to pokazano na slajdzie obok. | |valign="top"|Przyjmijmy oznaczenie bramy wejściowej cyfrą 1 a bramy wyjściowej cyfrą 2 jak to pokazano na slajdzie obok. | ||
| Linia 45: | Linia 43: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd4.png|500px]] | ||
|valign="top"|'''Transmitancja napięciowo-prądowa''' | |valign="top"|'''Transmitancja napięciowo-prądowa''' | ||
Transmitancja napięciowo-prądowa przyjmuje napięcie na dowolnym elemencie obwodu jako sygnał wyjściowy Y(s). Sygnałem wejściowym X(s) jest wymuszenie prądowe. Jest zatem zdefiniowana w postaci | Transmitancja napięciowo-prądowa przyjmuje napięcie na dowolnym elemencie obwodu jako sygnał wyjściowy <math>Y(s)</math>. Sygnałem wejściowym <math>X(s)</math> jest wymuszenie prądowe. Jest zatem zdefiniowana w postaci | ||
: <math>T_{ui}(s)=\frac{U_2(s)}{I_1(s)}</math> | : <math>T_{ui}(s)=\frac{U_2(s)}{I_1(s)}</math> | ||
| Linia 57: | Linia 55: | ||
'''Transmitancja prądowo-napięciowa''' | '''Transmitancja prądowo-napięciowa''' | ||
Transmitancję prądowo-napięciową definiuje się jako stosunek prądu wyjściowego do napięcia wejściowego (sygnałem wejściowym X(s) jest napięcie wymuszające a sygnałem wyjściowym Y(s) prąd dowolnego elementu w obwodzie) | Transmitancję prądowo-napięciową definiuje się jako stosunek prądu wyjściowego do napięcia wejściowego (sygnałem wejściowym <math>X(s)</math> jest napięcie wymuszające a sygnałem wyjściowym <math>Y(s)</math> prąd dowolnego elementu w obwodzie) | ||
: <math>T_{iu}(s)=\frac{I_2(s)}{U_1(s)}</math> | : <math>T_{iu}(s)=\frac{I_2(s)}{U_1(s)}</math> | ||
| Linia 71: | Linia 69: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd5.png|500px]] | ||
|valign="top"|Przy założeniu zerowych warunków początkowych dla indukcyjności i pojemności modele tych elementów nie zawierają źródeł a jedynie impedancje operatorowe Z(s). Zestaw impedancji operatorowych dla elementów pasywnych przedstawiono na slajdzie 5. | |valign="top"|Przy założeniu zerowych warunków początkowych dla indukcyjności i pojemności modele tych elementów nie zawierają źródeł a jedynie impedancje operatorowe <math>Z(s)</math>. Zestaw impedancji operatorowych dla elementów pasywnych przedstawiono na slajdzie 5. | ||
Dla obwodów pasywnych zawierających elementy R, L, C i M obliczenie transmitancji operatorowej polega na zastąpieniu elementu rzeczywistego poprzez ich impedancje operatorowe a następnie wykorzystując dowolną metodę analizy (metoda praw Kirchhoffa, węzłowa, oczkowa, Thevenina, Nortona) należy wyznaczyć odpowiedź operatorową w funkcji wymuszenia. | Dla obwodów pasywnych zawierających elementy <math>R</math>, <math>L</math>, <math>C</math> i <math>M</math> obliczenie transmitancji operatorowej polega na zastąpieniu elementu rzeczywistego poprzez ich impedancje operatorowe a następnie wykorzystując dowolną metodę analizy (metoda praw Kirchhoffa, węzłowa, oczkowa, Thevenina, Nortona) należy wyznaczyć odpowiedź operatorową w funkcji wymuszenia. | ||
W ogólnym przypadku obwodu elektrycznego liniowego zawierającego rezystory, cewki i kondensatory oraz źródła sterowane dowolna transmitancja operatorowa ma postać funkcji wymiernej o stopniu licznika równym m i stopniu mianownika równym n | W ogólnym przypadku obwodu elektrycznego liniowego zawierającego rezystory, cewki i kondensatory oraz źródła sterowane dowolna transmitancja operatorowa ma postać funkcji wymiernej o stopniu licznika równym <math>m</math> i stopniu mianownika równym <math>n</math>. | ||
: <math>T(s)=\frac{L(s)}{M(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}</math> | : <math>T(s)=\frac{L(s)}{M(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}</math> | ||
| Linia 94: | Linia 92: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd6.png|500px]] | ||
|valign="top"|'''Odpowiedzią impulsową''' układu nazywamy jego odpowiedź czasową na wymuszenie w postaci impulsu Diraca przy zerowych warunkach początkowych obwodu. Dla wyznaczenia odpowiedzi impulsowej wykorzystuje się pojęcie transmitancji operatorowej T(s). Transformata funkcji impulsowej Diraca jest równa 1, zatem obliczając odpowiedź obwodu przyjmiemy wymuszenie X(s)=1. Bezpośrednio z definicji transmitancji wynika | |valign="top"|'''Odpowiedzią impulsową''' układu nazywamy jego odpowiedź czasową na wymuszenie w postaci impulsu Diraca przy zerowych warunkach początkowych obwodu. Dla wyznaczenia odpowiedzi impulsowej wykorzystuje się pojęcie transmitancji operatorowej <math>T(s)</math>. Transformata funkcji impulsowej Diraca jest równa <math>1</math>, zatem obliczając odpowiedź obwodu przyjmiemy wymuszenie <math>X(s)=1</math>. Bezpośrednio z definicji transmitancji wynika | ||
: <math>T(s)=\frac{Y(s)}{X(s)}=\frac{Y(s)}{1}\rightarrow Y(s)=T(s)</math> | : <math>T(s)=\frac{Y(s)}{X(s)}=\frac{Y(s)}{1}\rightarrow Y(s)=T(s)</math> | ||
Odpowiedź impulsowa układu jest transformatą odwrotną Laplace’a sygnału Y(s). Stąd | Odpowiedź impulsowa układu jest transformatą odwrotną Laplace’a sygnału <math>Y(s)</math>. Stąd | ||
: <math>y(t)=L^{-1}\left[Y(s) \right]=L^{-1}\left[T(s) \right]</math> | : <math>y(t)=L^{-1}\left[Y(s) \right]=L^{-1}\left[T(s) \right]</math> | ||
Z powyższej zależności wynika, że odpowiedź impulsowa jest transformatą odwrotną Laplace’a transmitancji operatorowej T(s) układu. | Z powyższej zależności wynika, że odpowiedź impulsowa jest transformatą odwrotną Laplace’a transmitancji operatorowej <math>T(s)</math> układu. | ||
| Linia 110: | Linia 108: | ||
: <math>T(s)=\frac{Y(s)}{X(s)}=\frac{Y(s)}{1/s}\rightarrow Y(s)=\frac{1}{s}T(s)</math> | : <math>T(s)=\frac{Y(s)}{X(s)}=\frac{Y(s)}{1/s}\rightarrow Y(s)=\frac{1}{s}T(s)</math> | ||
Odpowiedź skokowa jest transformatą odwrotną Laplace’a sygnału Y(s). Stąd | Odpowiedź skokowa jest transformatą odwrotną Laplace’a sygnału <math>Y(s)</math>. Stąd | ||
: <math>y(t)=L^{-1}\left[Y(s) \right]=L^{-1}\left[\frac{1}{s} T(s) \right]</math> | : <math>y(t)=L^{-1}\left[Y(s) \right]=L^{-1}\left[\frac{1}{s} T(s) \right]</math> | ||
Odpowiedź skokowa układu jest więc transformatą odwrotną Laplace’a transmitancji operatorowej T(s) tego układu, podzielonej przez zmienną zespoloną s. Podobnie jak odpowiedź impulsowa odpowiedź skokowa jest określona w pełni przez transmitancję operatorową T(s) układu. | Odpowiedź skokowa układu jest więc transformatą odwrotną Laplace’a transmitancji operatorowej <math>T(s)</math> tego układu, podzielonej przez zmienną zespoloną <math>s</math>. Podobnie jak odpowiedź impulsowa odpowiedź skokowa jest określona w pełni przez transmitancję operatorową <math>T(s)</math> układu. | ||
|} | |} | ||
| Linia 120: | Linia 118: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd7.png|500px]] | ||
|valign="top"|Dla zilustrowania rozważań teoretycznych obliczmy odpowiedź impulsową i skokową układu o zadanej transmitancji operatorowej | |valign="top"|Dla zilustrowania rozważań teoretycznych obliczmy odpowiedź impulsową i skokową układu o zadanej transmitancji operatorowej | ||
| Linia 128: | Linia 126: | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
Stosując metodę residuów dla zadanej postaci transmitancji T(s) otrzymujemy: | Stosując metodę residuów dla zadanej postaci transmitancji <math>T(s)</math> otrzymujemy: | ||
* odpowiedź impulsową | * odpowiedź impulsową | ||
| Linia 149: | Linia 147: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd8.png|500px]] | ||
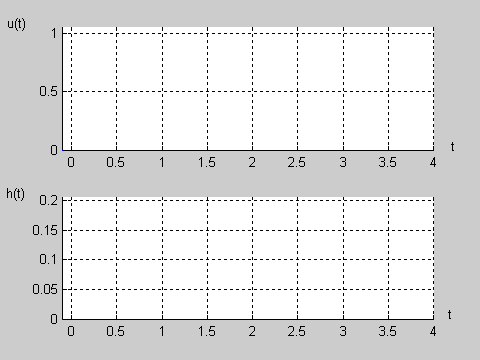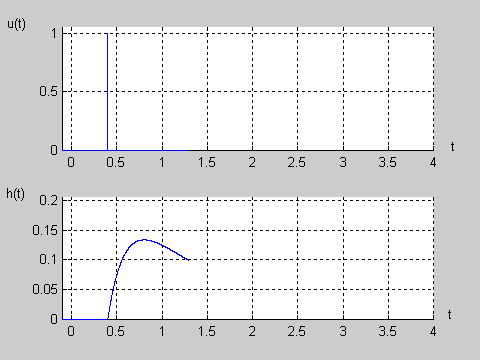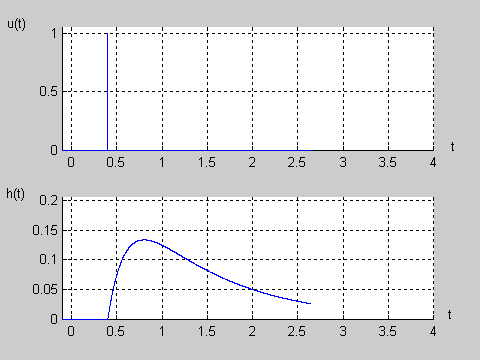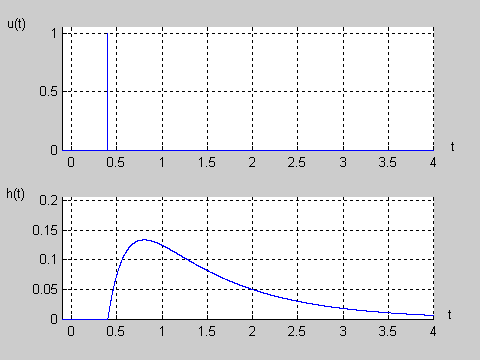
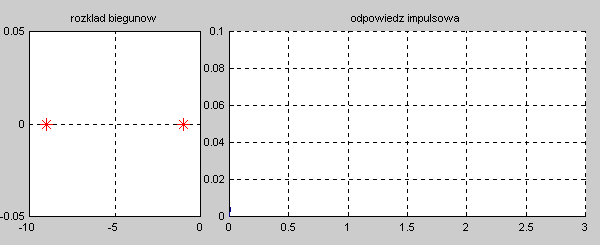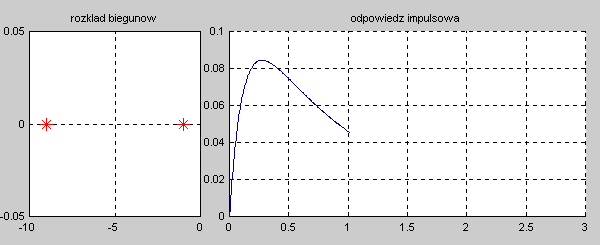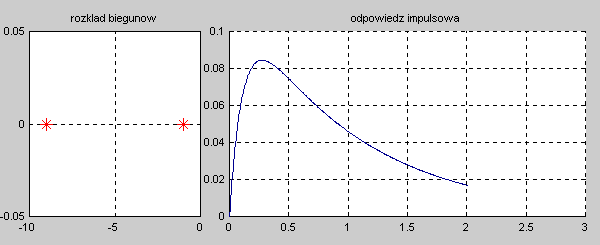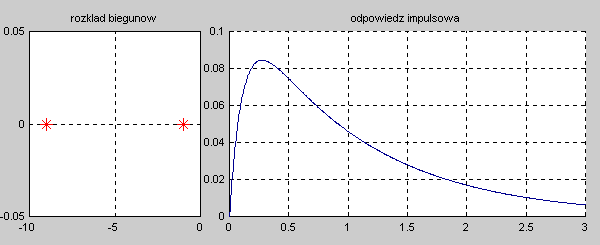
|valign="top"|Na slajdzie obok przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej T(s). | |valign="top"|Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej <math>T(s)</math>. | ||
[[Grafika:PEE_M9rys9_2a_animacja.gif]] | |||
[[Grafika:PEE_M9rys9_2b_animacja.gif]] | |||
|} | |} | ||
| Linia 156: | Linia 160: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd9.png|500px]] | ||
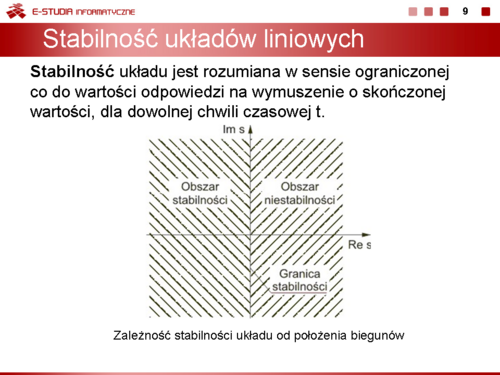
|valign="top"|'''Stabilność układu''' jest rozumiana w sensie ograniczonej co do wartości odpowiedzi na wymuszenie o skończonej wartości, dla dowolnej chwili czasowej t. Układ nazywać będziemy stabilnym, jeśli jego odpowiedź czasowa na skończoną wartość pobudzenia będzie ograniczona co do wartości w dowolnej chwili czasowej t. Stabilność wymaga, aby przy zaniku pobudzenia odpowiedź układu w stanie ustalonym przy <math>t \to \infty</math> była ograniczona co do wartości (stabilność w sensie zwykłym) lub zerowa (stabilność w sensie asymptotycznym). Oznacza to, że dla układów stabilnych odpowiedź w stanie przejściowym powinna zanikać do zera lub co najmniej nie narastać, pozostając na ustalonym poziomie. | |valign="top"|'''Stabilność układu''' jest rozumiana w sensie ograniczonej co do wartości odpowiedzi na wymuszenie o skończonej wartości, dla dowolnej chwili czasowej <math>t</math>. Układ nazywać będziemy stabilnym, jeśli jego odpowiedź czasowa na skończoną wartość pobudzenia będzie ograniczona co do wartości w dowolnej chwili czasowej <math>t</math>. Stabilność wymaga, aby przy zaniku pobudzenia odpowiedź układu w stanie ustalonym przy <math>t \to \infty</math> była ograniczona co do wartości (stabilność w sensie zwykłym) lub zerowa (stabilność w sensie asymptotycznym). Oznacza to, że dla układów stabilnych odpowiedź w stanie przejściowym powinna zanikać do zera lub co najmniej nie narastać, pozostając na ustalonym poziomie. | ||
Stabilność układu może więc być oceniana na podstawie odpowiedzi impulsowej. Jeśli odpowiedź ta zanika do zera lub pozostaje na stałym poziomie przy <math>t \to \infty</math> układ jest stabilny. Jeśli natomiast odpowiedź impulsowa ma charakter narastający w czasie – układ jest niestabilny. Zauważmy, że odpowiedź impulsowa jest transformatą odwrotną Laplace’a transmitancji operatorowej <math>h(t)=L^{-1} \left[ T(s)\right]</math>. Jeśli bieguny układu oznaczymy przez <math>s_i</math> gdzie i = 1, 2, ..., n, wówczas w przypadku biegunów jednokrotnych na podstawie metody residuów odpowiedź impulsowa może być wyrażona wzorem | Stabilność układu może więc być oceniana na podstawie odpowiedzi impulsowej. Jeśli odpowiedź ta zanika do zera lub pozostaje na stałym poziomie przy <math>t \to \infty</math> układ jest stabilny. Jeśli natomiast odpowiedź impulsowa ma charakter narastający w czasie – układ jest niestabilny. Zauważmy, że odpowiedź impulsowa jest transformatą odwrotną Laplace’a transmitancji operatorowej <math>h(t)=L^{-1} \left[ T(s)\right]</math>. Jeśli bieguny układu oznaczymy przez <math>s_i</math> gdzie <math>i = 1, 2, ..., n</math>, wówczas w przypadku biegunów jednokrotnych na podstawie metody residuów odpowiedź impulsowa może być wyrażona wzorem | ||
: <math>h(t)=\sum_{i=1}^n {A_ie^{s_it}}</math> | : <math>h(t)=\sum_{i=1}^n {A_ie^{s_it}}</math> | ||
Wzór ten dowodzi, że jeśli wszystkie bieguny układu są położone wyłącznie w lewej półpłaszczyźnie zmiennej zespolonej s, <math>Re(s_i) \le 0</math>, wówczas odpowiedź impulsowa zanika z czasem do zera lub pozostaje ograniczona co do amplitudy (gdy część biegunów lub wszystkie znajdą się na osi urojonej). Sytuacja jest nieco bardziej złożona, gdy część biegunów jest wielokrotna. Dla uproszczenia ograniczymy się tylko do biegunów dwukrotnych. Załóżmy, że liczba takich dwukrotnych biegunów jest równa m. W takim przypadku zastosowanie wzorów na residuum przy obliczaniu transformaty odwrotnej prowadzi do wyniku | Wzór ten dowodzi, że jeśli wszystkie bieguny układu są położone wyłącznie w lewej półpłaszczyźnie zmiennej zespolonej <math>s</math>, <math>Re(s_i) \le 0</math>, wówczas odpowiedź impulsowa zanika z czasem do zera lub pozostaje ograniczona co do amplitudy (gdy część biegunów lub wszystkie znajdą się na osi urojonej). Sytuacja jest nieco bardziej złożona, gdy część biegunów jest wielokrotna. Dla uproszczenia ograniczymy się tylko do biegunów dwukrotnych. Załóżmy, że liczba takich dwukrotnych biegunów jest równa <math>m</math>. W takim przypadku zastosowanie wzorów na residuum przy obliczaniu transformaty odwrotnej prowadzi do wyniku | ||
: <math>y(t)=\sum_{i=1}^n {A_ie^{s_it}}+\sum_{k=1}^m {B_kte^{s_kt}}</math> | : <math>y(t)=\sum_{i=1}^n {A_ie^{s_it}}+\sum_{k=1}^m {B_kte^{s_kt}}</math> | ||
| Linia 175: | Linia 179: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd10.png|500px]] | ||
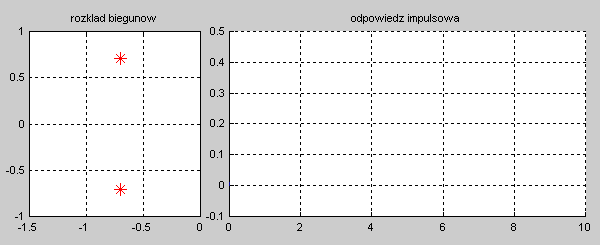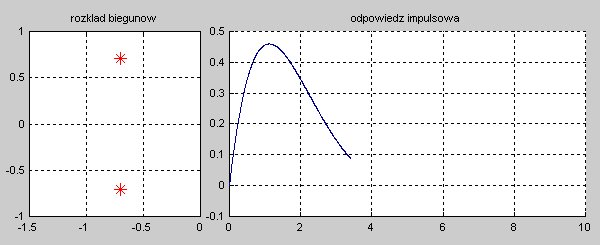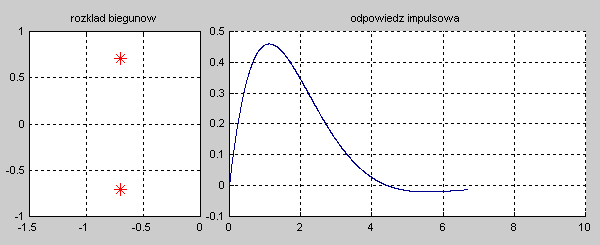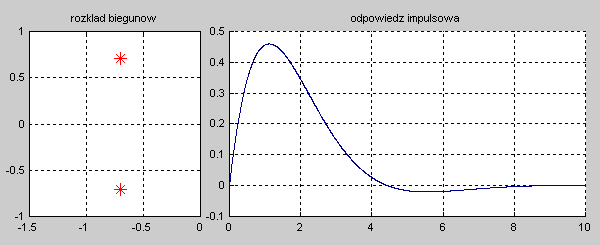
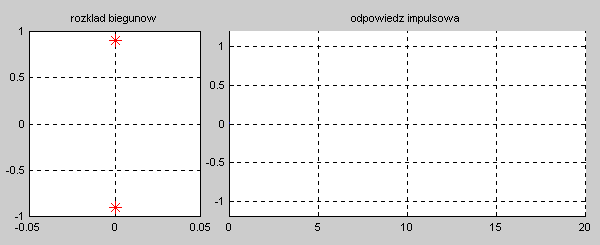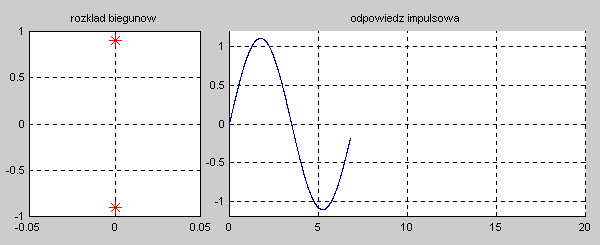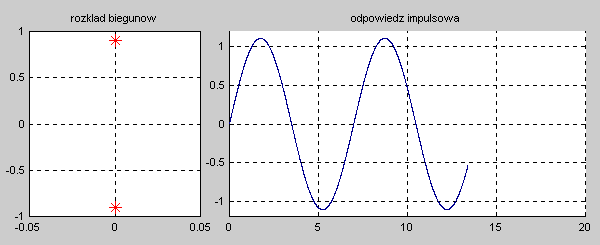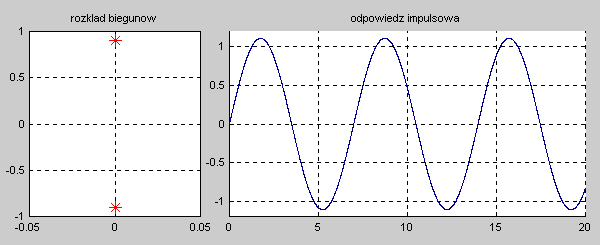
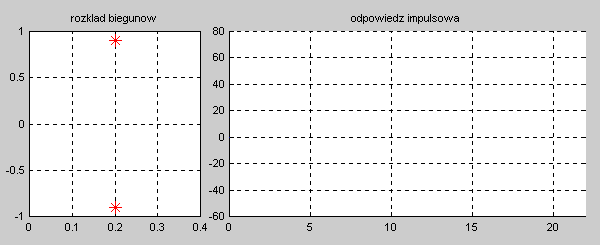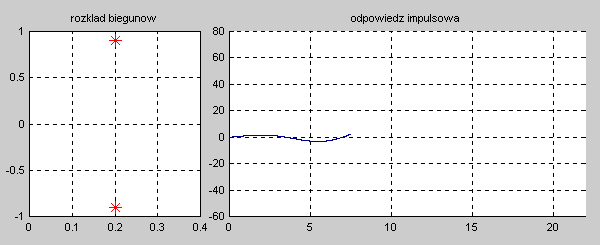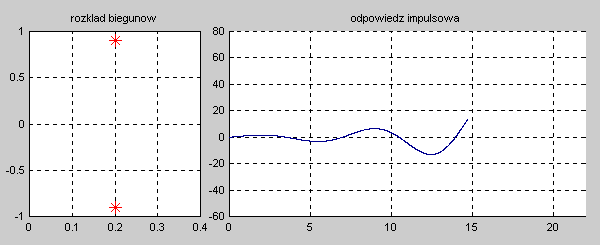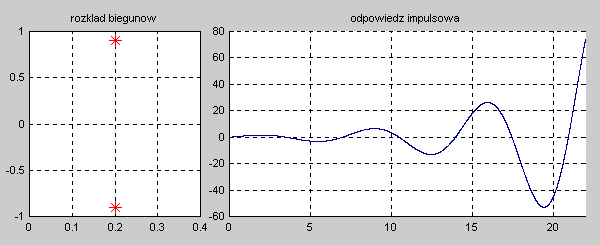
|valign="top"|Na slajdzie obok i poniższych animacjach zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). | |valign="top"|Na slajdzie obok i poniższych animacjach zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). | ||
[[Grafika: | [[Grafika:PEE_M9_rys_9_4a_animacja.gif]] | ||
[[Grafika: | [[Grafika:PEE_M9_rys_9_4b_animacja.gif]] | ||
[[Grafika: | [[Grafika:PEE_M9_rys_9_4c_animacja.gif]] | ||
[[Grafika: | [[Grafika:PEE_M9_rys_9_4d_animacja.gif]] | ||
W zależności od wartości biegunów mamy do czynienia ze stanem aperiodycznym (bieguny położone na osi rzeczywistej) oraz oscylacyjnym (bieguny zespolone). Zanikanie odpowiedzi impulsowej do zera świadczy o stabilności asymptotycznej układu. Odpowiedź o ograniczonej amplitudzie nie zanikająca z czasem świadczy o stabilności zwykłej układu. Odpowiedź narastająca z czasem jest cechą układu niestabilnego. | W zależności od wartości biegunów mamy do czynienia ze stanem aperiodycznym (bieguny położone na osi rzeczywistej) oraz oscylacyjnym (bieguny zespolone). Zanikanie odpowiedzi impulsowej do zera świadczy o stabilności asymptotycznej układu. Odpowiedź o ograniczonej amplitudzie nie zanikająca z czasem świadczy o stabilności zwykłej układu. Odpowiedź narastająca z czasem jest cechą układu niestabilnego. | ||
| Linia 192: | Linia 196: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd11.png|500px]] | ||
|valign="top"|'''Charakterystyką częstotliwościową''' układu nazywać będziemy zależność wartości sygnału wyjściowego tego układu od częstotliwości przy jednostkowym wymuszeniu sinusoidalnym przyłożonym na wejście układu. Charakterystykę tę można wyznaczyć bezpośrednio na podstawie transmitancji operatorowej T(s). Nosi ona nazwę '''transmitancji widmowej''' układu. | |valign="top"|'''Charakterystyką częstotliwościową''' układu nazywać będziemy zależność wartości sygnału wyjściowego tego układu od częstotliwości przy jednostkowym wymuszeniu sinusoidalnym przyłożonym na wejście układu. Charakterystykę tę można wyznaczyć bezpośrednio na podstawie transmitancji operatorowej T(s). Nosi ona nazwę '''transmitancji widmowej''' układu. | ||
| Linia 199: | Linia 203: | ||
: <math>T(j\omega)=T(s)|_{s=j\omega}</math> | : <math>T(j\omega)=T(s)|_{s=j\omega}</math> | ||
Transmitancja widmowa reprezentuje sobą liczbę zespoloną będącą funkcją pulsacji <math>\omega\ | Transmitancja widmowa reprezentuje sobą liczbę zespoloną będącą funkcją pulsacji <math>\omega\ </math>,. Przedstawiając ją w postaci wykładniczej, to jest <math>T(j\omega)=|T(j\omega)|e^{j\varphi (\omega)}</math> można zdefiniować dwa rodzaje charakterystyk częstotliwościowych: | ||
* '''charakterystyka amplitudowa''' przedstawia sobą zależność modułu transmitancji widmowej <math>T(j\omega)</math> od pulsacji <math>\omega\ | * '''charakterystyka amplitudowa''' przedstawia sobą zależność modułu transmitancji widmowej <math>T(j\omega)</math> od pulsacji <math>\omega\ </math>, (częstotliwości f), to jest <math>|T(j\omega)|</math> | ||
* '''charakterystyka fazowa''' określa zależność argumentu transmitancji widmowej <math>T(j\omega)</math> od pulsacji (częstotliwości) to jest <math>\varphi (\omega)</math>. Charakterystyka fazowa reprezentuje sobą przesunięcie fazowe między sygnałem wejściowym a wyjściowym dla danej pulsacji <math>\omega\ | * '''charakterystyka fazowa''' określa zależność argumentu transmitancji widmowej <math>T(j\omega)</math> od pulsacji (częstotliwości) to jest <math>\varphi (\omega)</math>. Charakterystyka fazowa reprezentuje sobą przesunięcie fazowe między sygnałem wejściowym a wyjściowym dla danej pulsacji <math>\omega\ </math>,. | ||
Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\ | Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\ </math>, do <math>10^6</math>) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując '''logarytmiczną charakterystykę amplitudową''' | ||
: <math>20log_{10}(|T(j\omega)|)</math> | : <math>20log_{10}(|T(j\omega)|)</math> | ||
| Linia 214: | Linia 218: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd12.png|500px]] | ||
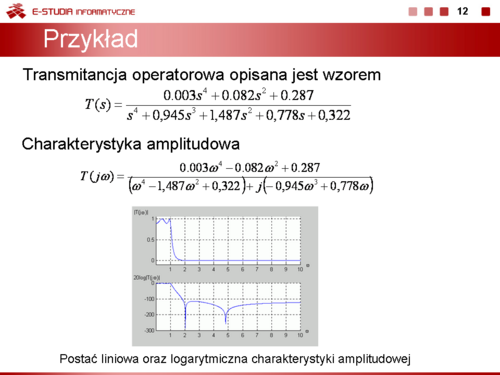
|valign="top"|Jako przykład rozpatrzmy transmitancję operatorową opisaną wzorem | |valign="top"|Jako przykład rozpatrzmy transmitancję operatorową opisaną wzorem | ||
<math>T(s)=\frac{0,003s^4+0,082s^2+0,287}{s^4+0,945s^3+1,487s^2+0,778s+0,322}</math> | : <math>T(s)=\frac{0,003s^4+0,082s^2+0,287}{s^4+0,945s^3+1,487s^2+0,778s+0,322}</math> | ||
Charakterystyka amplitudowa jest określona wzorem | Charakterystyka amplitudowa jest określona wzorem | ||
<math>T(s)=\frac{0,003\omega^4-0,082\omega^2+0,287}{(\omega^4-1,487\omega^2+0,322)+j(-0,945\omega^3+0,778\omega)}</math> | : <math>T(s)=\frac{0,003\omega^4-0,082\omega^2+0,287}{(\omega^4-1,487\omega^2+0,322)+j(-0,945\omega^3+0,778\omega)}</math> | ||
Na slajdzie przedstawiono przykładowo charakterystykę amplitudową oraz logarytmiczną charakterystykę amplitudową odpowiadającą transmitancji danej wzorem. | Na slajdzie i animacji przedstawiono przykładowo charakterystykę amplitudową oraz logarytmiczną charakterystykę amplitudową odpowiadającą transmitancji danej wzorem. | ||
[[Grafika:PEE_M9_rys_9_5_animacja.gif]] | |||
Każdy rodzaj przedstawienia charakterystyki amplitudowej podkreśla inne szczegóły w jej przebiegu. Charakterystyka logarytmiczna podkreśla stosunkowo niewielkie w skali globalnej zmiany dynamiczne w tak zwanym paśmie zaporowym, gdzie amplituda sygnału jest bardzo mała w stosunku do pasma przepustowego, podczas gdy skala liniowa uwypukla globalny charakter przebiegu tracąc drobne szczegóły w zakresie częstotliwości gdzie wartości sygnałów są małe. | Każdy rodzaj przedstawienia charakterystyki amplitudowej podkreśla inne szczegóły w jej przebiegu. Charakterystyka logarytmiczna podkreśla stosunkowo niewielkie w skali globalnej zmiany dynamiczne w tak zwanym paśmie zaporowym, gdzie amplituda sygnału jest bardzo mała w stosunku do pasma przepustowego, podczas gdy skala liniowa uwypukla globalny charakter przebiegu tracąc drobne szczegóły w zakresie częstotliwości gdzie wartości sygnałów są małe. | ||
| Linia 234: | Linia 243: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd13.png|500px]] | ||
|valign="top"|W praktyce inżynierskiej zdefiniowano wiele użytecznych postaci transmitancji operatorowych. Tutaj ograniczymy się jedynie do trzech najprostszych transmitancji pierwszego rzędu: układu całkującego, różniczkującego oraz przesuwnika fazowego. | |valign="top"|W praktyce inżynierskiej zdefiniowano wiele użytecznych postaci transmitancji operatorowych. Tutaj ograniczymy się jedynie do trzech najprostszych transmitancji pierwszego rzędu: układu całkującego, różniczkującego oraz przesuwnika fazowego. | ||
| Linia 244: | Linia 253: | ||
: <math>T(s)=\frac{k}{s}</math> | : <math>T(s)=\frac{k}{s}</math> | ||
Układ nosi nazwę całkującego, gdyż operator 1/s w dziedzinie częstotliwości zespolonej Laplace’a oznacza całkowanie funkcji w dziedzinie czasu. Charakterystykę częstotliwościową układu całkującego opisuje zależność | Układ nosi nazwę całkującego, gdyż operator <math>1/s</math> w dziedzinie częstotliwości zespolonej Laplace’a oznacza całkowanie funkcji w dziedzinie czasu. Charakterystykę częstotliwościową układu całkującego opisuje zależność | ||
: <math>T(j\omega)=\frac{k}{j\omega}=\frac{k}{\omega}e^{-j90^\circ}</math> | : <math>T(j\omega)=\frac{k}{j\omega}=\frac{k}{\omega}e^{-j90^\circ}</math> | ||
| Linia 256: | Linia 265: | ||
: <math>\varphi(\omega)=-90^\circ</math> | : <math>\varphi(\omega)=-90^\circ</math> | ||
dla układu całkującego przy k>0 przedstawiono na slajdzie obok. | dla układu całkującego przy <math>k>0</math> przedstawiono na slajdzie obok i animacji poniżej. | ||
[[Grafika:PEE_M9_rys_9_6_animacja.gif]] | |||
Charakterystyka amplitudowa jest typu hiperbolicznego, a charakterystyka fazowa stała (przesunięcie fazowe stałe i równe <math>-90^\circ</math> niezależnie od częstotliwości). | Charakterystyka amplitudowa jest typu hiperbolicznego, a charakterystyka fazowa stała (przesunięcie fazowe stałe i równe <math>-90^\circ</math> niezależnie od częstotliwości). | ||
| Linia 264: | Linia 277: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd14.png|500px]] | ||
|valign="top"|'''Układ różniczkujący''' | |valign="top"|'''Układ różniczkujący''' | ||
| Linia 271: | Linia 284: | ||
: <math>T(s)=ks</math> | : <math>T(s)=ks</math> | ||
Układ nosi nazwę różniczkującego, gdyż operator s w dziedzinie częstotliwości zespolonej oznacza różniczkowanie funkcji w dziedzinie czasu. Charakterystyka częstotliwościowa opisana jest zależnością | Układ nosi nazwę różniczkującego, gdyż operator <math>s</math> w dziedzinie częstotliwości zespolonej oznacza różniczkowanie funkcji w dziedzinie czasu. Charakterystyka częstotliwościowa opisana jest zależnością | ||
: <math>T(j\omega)=kj\omega=k\omega e^{j90^\circ}</math> | : <math>T(j\omega)=kj\omega=k\omega e^{j90^\circ}</math> | ||
| Linia 283: | Linia 296: | ||
: <math>\varphi(\omega)=90^\circ</math> | : <math>\varphi(\omega)=90^\circ</math> | ||
Wykres obu charakterystyk układu różniczkującego przy k>0 przedstawiono na slajdzie obok. | Wykres obu charakterystyk układu różniczkującego przy <math>k>0</math> przedstawiono na slajdzie obok i animacji poniżej. | ||
|} | |||
[[Grafika:PEE_M9_rys_9_7_animacja.gif]] | |||
|} | |||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd15.png|500px]] | ||
|valign="top"|'''Przesuwnik fazowy''' | |valign="top"|'''Przesuwnik fazowy''' | ||
| Linia 307: | Linia 323: | ||
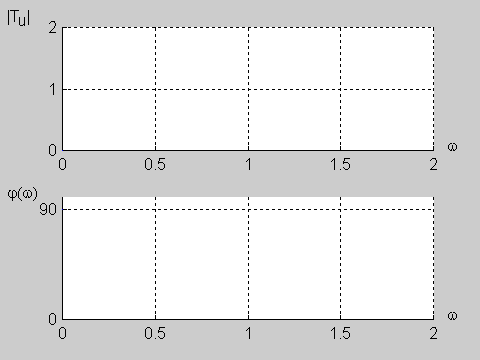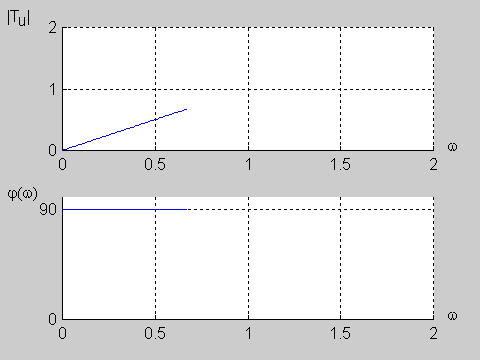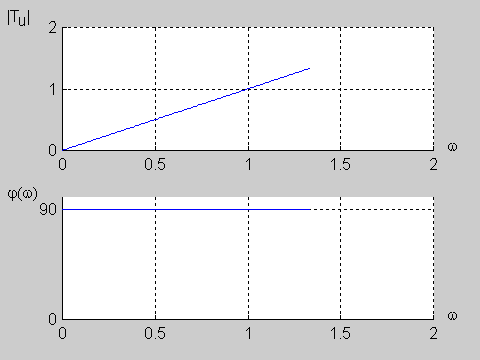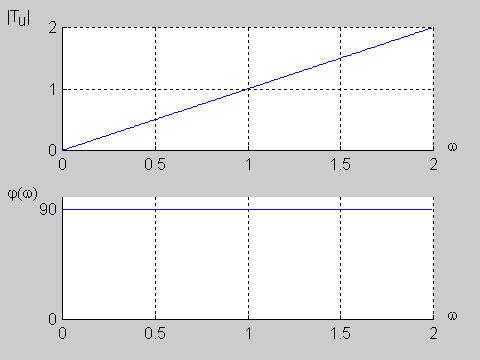
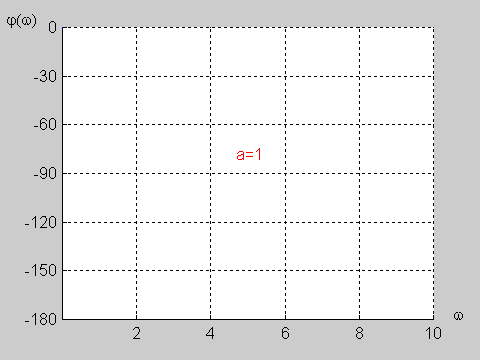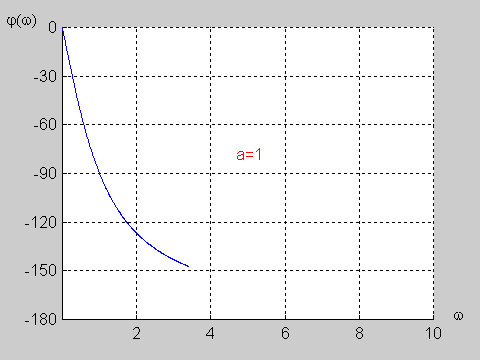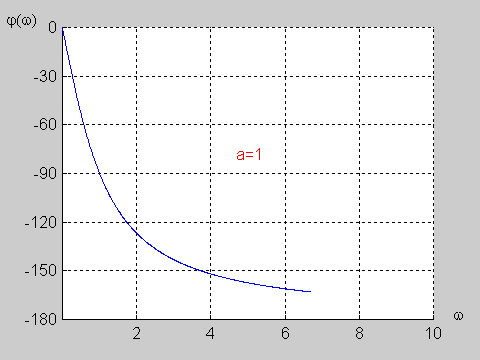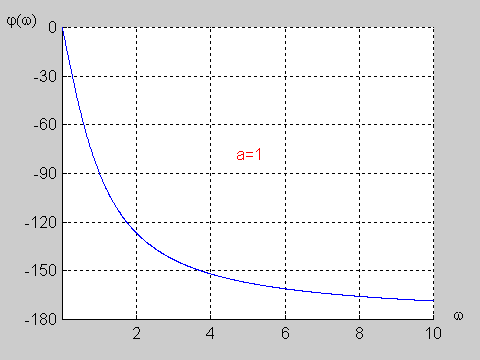
Na slajdzie obok i poniższej animacji przedstawiono wykres charakterystyki fazowej przesuwnika w funkcji pulsacji dla wartości a=1. | Na slajdzie obok i poniższej animacji przedstawiono wykres charakterystyki fazowej przesuwnika w funkcji pulsacji dla wartości <math>a=1</math>. | ||
{| | {| | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M9_rys9_8_animacja.gif]] | ||
|} | |} | ||
|} | |} | ||
| Linia 317: | Linia 334: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd16.png|500px]] | ||
|valign="top"|Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem | |valign="top"|Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem | ||
| Linia 324: | Linia 341: | ||
Załączony do podręcznika program interakcyjny '''CHARAKTERYSTYKI''' umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. | Załączony do podręcznika program interakcyjny '''CHARAKTERYSTYKI''' umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. | ||
Transmitancja widmowa <math>T(j\omega)</math> takiego układu wyznaczana jest z transmitancji operatorowej <math>T(s)\ | Transmitancja widmowa <math>T(j\omega)</math> takiego układu wyznaczana jest z transmitancji operatorowej <math>T(s)\ </math>, przez podstawienie <math>s=j\omega</math>. W wyniku otrzymuje się | ||
: <math>T(s)=\frac{b_m(j\omega)^m+b_{m-1}(j\omega)^{m-1}+...+b_1j\omega+b_0}{a_n(j\omega)^n+a_{n-1}(j\omega)^{n-1}+...+a_1j\omega+a_0}</math> | : <math>T(s)=\frac{b_m(j\omega)^m+b_{m-1}(j\omega)^{m-1}+...+b_1j\omega+b_0}{a_n(j\omega)^n+a_{n-1}(j\omega)^{n-1}+...+a_1j\omega+a_0}</math> | ||
| Linia 332: | Linia 349: | ||
: <math>T(j\omega)=A(\omega)+jB(\omega)</math> | : <math>T(j\omega)=A(\omega)+jB(\omega)</math> | ||
Część rzeczywista <math>A(\omega)</math> i urojona <math>B(\omega)</math> są funkcjami zarówno współczynników <math>a_i</math>, <math>b_i</math> licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji <math>\omega\ | Część rzeczywista <math>A(\omega)</math> i urojona <math>B(\omega)</math> są funkcjami zarówno współczynników <math>a_i</math>, <math>b_i</math> licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji <math>\omega\ </math>,. Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem | ||
: <math>|T(j\omega)|=\sqrt{A^2(\omega)+B^2(\omega)}</math> | : <math>|T(j\omega)|=\sqrt{A^2(\omega)+B^2(\omega)}</math> | ||
| Linia 339: | Linia 356: | ||
: <math>\varphi (\omega)=arctg \left(\frac{B(\omega)}{A(\omega)}\right)</math> | : <math>\varphi (\omega)=arctg \left(\frac{B(\omega)}{A(\omega)}\right)</math> | ||
|} | |} | ||
| Linia 348: | Linia 363: | ||
|valign="top" width="500px"|<applet code="filtr.class" archive="images/6/6a/PEE_M9_filtr.jar" width="462" height="363"> | |valign="top" width="500px"|<applet code="filtr.class" archive="images/6/6a/PEE_M9_filtr.jar" width="462" height="363"> | ||
</applet> | </applet> | ||
|valign="top"|Omawiane zależności zostały wykorzystane do badania charakterystyk częstotliwościowych układów opisanych transmitancją operatorową T(s) zadawaną przez użytkownika. | |valign="top"|Omawiane zależności zostały wykorzystane do badania charakterystyk częstotliwościowych układów opisanych transmitancją operatorową <math>T(s)</math> zadawaną przez użytkownika. | ||
Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. | Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. | ||
| Linia 358: | Linia 373: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd17.png|500px]] | ||
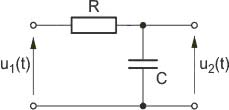
|valign="top"| | |valign="top"|Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: <math>R=1\Omega</math>, <math>L=2H\ </math>,, <math>C=1F\ </math>,. | ||
Schemat operatorowy obwodu przy zerowych warunkach początkowych stosowany do wyznaczenia transmitancji przedstawiony jest na dolnym rysunku. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd18.png|500px]] | |||
|valign="top"|Kolejne etapy wyznaczania transmitancji: | |||
Kolejne etapy wyznaczania transmitancji: | |||
Prąd I(s) | Prąd I(s) | ||
<math>I(s)=\frac{U_1(s)}{R+sL+1/sC}=\frac{sC}{s^2LC+sRC+1}U_1(s)</math> | : <math>I(s)=\frac{U_1(s)}{R+sL+1/sC}=\frac{sC}{s^2LC+sRC+1}U_1(s)</math> | ||
Napięcie wyjściowe | Napięcie wyjściowe | ||
<math>U_2(s)=\frac{1}{sC}I(s)=\frac{sC}{s^2LC+sRC+1}U_1(s)</math> | : <math>U_2(s)=\frac{1}{sC}I(s)=\frac{sC}{s^2LC+sRC+1}U_1(s)</math> | ||
Transmitancja napięciowa | Transmitancja napięciowa | ||
| Linia 387: | Linia 401: | ||
: <math>T_u(s)=\frac{0,5}{s^2+0,5s+0,5}</math> | : <math>T_u(s)=\frac{0,5}{s^2+0,5s+0,5}</math> | ||
|} | |} | ||
| Linia 393: | Linia 406: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
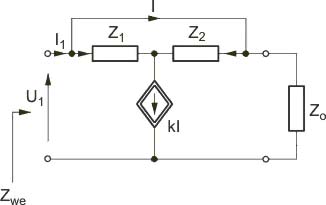
|valign="top"|'''Zadania sprawdzające''' | |||
''Zadanie 9.1'' | |||
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na poniższym rysunku. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową. | |||
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na | |||
{| | {| | ||
| Linia 407: | Linia 419: | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
Z prawa prądowego i napięciowego Kirchhoffa napisanych dla obwodu z | Z prawa prądowego i napięciowego Kirchhoffa napisanych dla obwodu z powyzszego rysunku otrzymuje się | ||
: <math>-U_1+Z_1(I_1-I)=Z_2(I-Y_0U_1)-U_1</math> | : <math>-U_1+Z_1(I_1-I)=Z_2(I-Y_0U_1)-U_1</math> | ||
| Linia 416: | Linia 427: | ||
gdzie <math>Y_0=1/Z_0</math>. Z równania drugiego otrzymuje się | gdzie <math>Y_0=1/Z_0</math>. Z równania drugiego otrzymuje się | ||
: <math>I=\frac{I_1-Y_0U_1}{k}</math> | : <math>I=\frac{I_1-Y_0U_1}{k}</math> | ||
| Linia 422: | Linia 432: | ||
Po podstawieniu do wzoru pierwszego otrzymujemy | Po podstawieniu do wzoru pierwszego otrzymujemy | ||
: <math>\frac{Z_1+Z_2-Z_1k}{k}I_1=\left(Z_2Y_0+\frac{Z_1+Z_2}{k}Y_0 \right)U_1</math> | : <math>\frac{Z_1+Z_2-Z_1k}{k}I_1=\left(Z_2Y_0+\frac{Z_1+Z_2}{k}Y_0 \right)U_1</math> | ||
| Linia 428: | Linia 437: | ||
Stąd | Stąd | ||
: <math>Z_{we}=\frac{U_1}{I_1}=\frac{Z_1+Z_2-Z_1k}{kZ_2Y_0+Y_0(Z_1+Z_2)}</math> | : <math>Z_{we}=\frac{U_1}{I_1}=\frac{Z_1+Z_2-Z_1k}{kZ_2Y_0+Y_0(Z_1+Z_2)}</math> | ||
''Zadanie 9. | ---- | ||
''Zadanie 9.2'' | |||
Wyznaczyć charakterystyki częstotliwościowe obwodu przedstawionego na | Wyznaczyć charakterystyki częstotliwościowe obwodu przedstawionego na poniższym rysunku biorąc pod uwagę transmitancję napięciową. | ||
{| | {| | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Rtxt3.jpg]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Rtxt3.jpg]] | ||
|} | |} | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
Transmitancja napięciowa obwodu określona jest wzorem | Transmitancja napięciowa obwodu określona jest wzorem | ||
: <math>T_u(s)=\frac{1/sC}{R+1/sC}=\frac{1}{sRC+1}</math> | : <math>T_u(s)=\frac{1/sC}{R+1/sC}=\frac{1}{sRC+1}</math> | ||
Transmitancja widmowa obwodu określona jest na podstawie transmitancji operatorowej <math>T_u(s)\ | Transmitancja widmowa obwodu określona jest na podstawie transmitancji operatorowej <math>T_u(s)\ </math>, przy założeniu <math>s=j\omega</math> | ||
: <math>T_u(j\omega)=\frac{1}{j\omega RC+1}</math> | : <math>T_u(j\omega)=\frac{1}{j\omega RC+1}</math> | ||
| Linia 456: | Linia 465: | ||
Charakterystyka amplitudowa | Charakterystyka amplitudowa | ||
: <math>|T_u(j\omega)|=\frac{1}{\sqrt{(\omega RC)^2+1}}</math> | : <math>|T_u(j\omega)|=\frac{1}{\sqrt{(\omega RC)^2+1}}</math> | ||
| Linia 462: | Linia 470: | ||
Charakterystyka fazowa | Charakterystyka fazowa | ||
: <math>\varphi (\omega)=-arctg(\omega RC)</math> | : <math>\varphi (\omega)=-arctg(\omega RC)</math> | ||
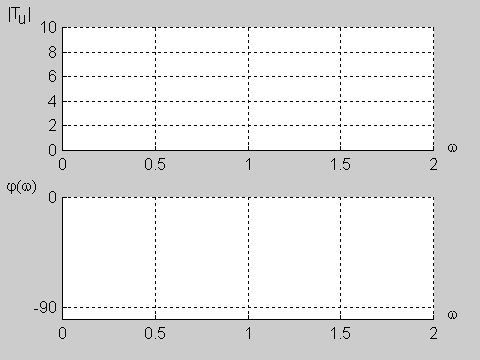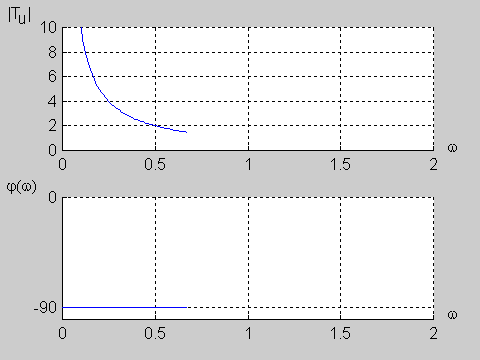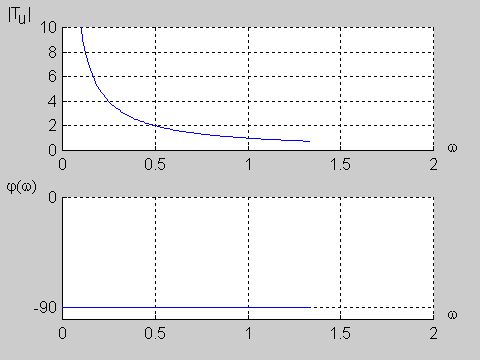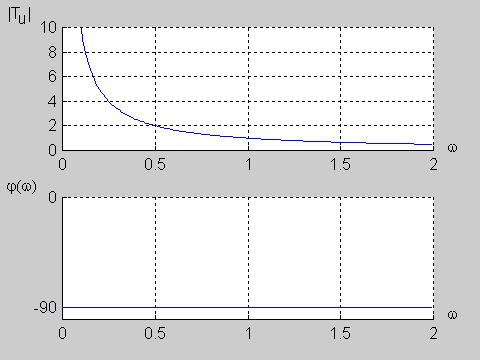
Na | Na poniższym rysunku przedstawiono charakterystykę amplitudową i fazową dla wartości jednostkowych elementów obwodu (<math>R=1\Omega</math> i <math>C=1F\ </math>,) | ||
{| | {| | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M9_rys_9_10.gif]] | ||
|} | |} | ||
Aktualna wersja na dzień 12:04, 5 wrz 2023

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |
|
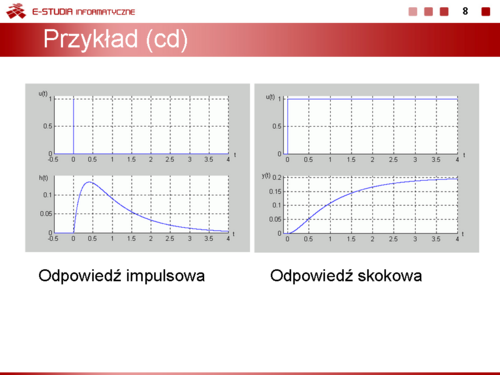
Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej . |

|
Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem
Załączony do podręcznika program interakcyjny CHARAKTERYSTYKI umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. Transmitancja widmowa takiego układu wyznaczana jest z transmitancji operatorowej , przez podstawienie . W wyniku otrzymuje się Transmitancja widmowa przedstawia sobą funkcję zespoloną pulsacji i może być zapisana w postaci ogólnej jako Część rzeczywista i urojona są funkcjami zarówno współczynników , licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji ,. Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem Charakterystyka fazowa jest fazą transmitancji widmowej i wyznaczana jest z zależności |
| <applet code="filtr.class" archive="images/6/6a/PEE_M9_filtr.jar" width="462" height="363">
</applet> |
Omawiane zależności zostały wykorzystane do badania charakterystyk częstotliwościowych układów opisanych transmitancją operatorową zadawaną przez użytkownika.
Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. Wykorzystując podane wcześniej zależności częstotliwościowe program wykreśla charakterystyki amplitudowe (liniową i logarytmiczną wyrażoną w decybelach) oraz charakterystykę fazową w stopniach. Charakterystyki filtru zostają wykreślone w oddzielnych oknach, pozwalających na skalowanie oraz oglądanie w powiększeniu poszczególnych odcinków krzywych. |
|
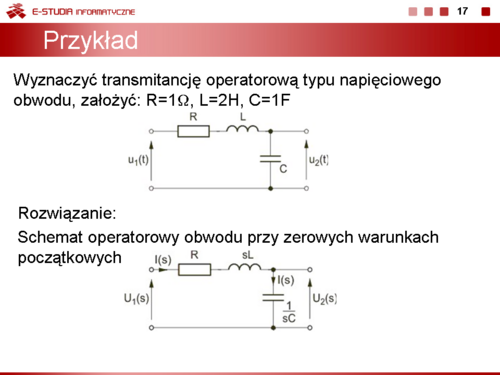
Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: , ,, ,.
|

|
Kolejne etapy wyznaczania transmitancji:
Prąd I(s) Napięcie wyjściowe Transmitancja napięciowa Po podstawieniu wartości liczbowych otrzymuje się |
| Zadania sprawdzające
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na poniższym rysunku. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową.
Rozwiązanie Z prawa prądowego i napięciowego Kirchhoffa napisanych dla obwodu z powyzszego rysunku otrzymuje się
Zadanie 9.2 Wyznaczyć charakterystyki częstotliwościowe obwodu przedstawionego na poniższym rysunku biorąc pod uwagę transmitancję napięciową.
Transmitancja napięciowa obwodu określona jest wzorem
|