Programowanie funkcyjne/Model obliczeń: Różnice pomiędzy wersjami
| (Nie pokazano 42 wersji utworzonych przez 3 użytkowników) | |||
| Linia 8: | Linia 8: | ||
== Środowisko i ramki == | == Środowisko i ramki == | ||
<p align="justify | <p align="justify> | ||
Przedstawiając podstawy Ocamla mówiliśmy o ''środowisku'' przypisującym nazwom | Przedstawiając podstawy Ocamla mówiliśmy o ''środowisku'' przypisującym nazwom stałe ich wartości. | ||
Dodatkowo takich środowisk może być wiele: środowisko zawierające wszystkie aktualnie globalnie zdefiniowane stałe, środowiska powstające na potrzeby definicji lokalnych i wywołań procedur. | Dodatkowo takich środowisk może być wiele: środowisko zawierające wszystkie aktualnie globalnie zdefiniowane stałe, środowiska powstające na potrzeby definicji lokalnych i wywołań procedur. | ||
</p> | </p> | ||
<p align="justify"> | <p align="justify"> | ||
Środowisko jest zrealizowane jako lista jednokierunkowa tzw. ''ramek''. | Środowisko jest zrealizowane jako lista jednokierunkowa, tzw. ''lista ramek''. | ||
Każda ramka zawiera identyfikator (lub identyfikatory) i ich wartości (lub wskaźniki do takich wartości) | Każda ramka zawiera identyfikator (lub identyfikatory) i ich wartości (lub wskaźniki do takich wartości) | ||
oraz wskaźnik do kolejnej ramki tworzącej środowisko. | oraz wskaźnik do kolejnej ramki tworzącej środowisko. | ||
Poszukując w środowisku wartości stałej, przeglądamy kolejne ramki środowiska. | Poszukując w środowisku wartości stałej, przeglądamy kolejne ramki środowiska. | ||
Pierwsza ramka, która zawiera nazwę stałej określa jej wartość. | Pierwsza ramka, która zawiera nazwę stałej, określa jej wartość. | ||
</p> | </p> | ||
<p align="justify"> | <p align="justify"> | ||
Dalej będziemy utożsamiać środowisko ze wskaźnikiem do pierwszej ramki tworzącej środowisko. | |||
Środowisko reprezentowane przez listę ramek bez pierwszej ramki będziemy nazywać ''środowiskiem otaczającym'', a wskaźnik prowadzący z jednej ramki do kolejnej będziemy nazywać ''wskaźnikiem do środowiska otaczającego''. | |||
</p> | |||
Każda | {{przyklad|[Dodawanie ramek do środowiska]||}} | ||
[[Image:Pf-rys-3-a.png||center]] | |||
== Definicje globalne == | |||
<p align="justify"> | |||
Prowadząc interakcję z kompilatorem, pracujemy w kontekście tzw. ''aktualnego środowiska (globalnego)''. | |||
Każda dodana definicja zmienia to środowisko. | |||
Zdefiniowanie nowych wartości powoduje dodanie nowej ramki zawierającej zdefiniowane wartości. | |||
Dotychczasowe środowisko staje się środowiskiem otaczającym tej ramki. | |||
Utworzona ramka staje się nowym aktualnym środowiskiem (globalnym). | |||
</p> | </p> | ||
= | <p align="justify"> | ||
Mechanizm ten pozwala na przesłanianie istniejących w środowisku stałych. | |||
Jeśli zdefiniujemy nową stałą o takiej samej nazwie, to będzie ona znajdowała się we wcześniejszej ramce i to właśnie ona będzie znajdowana w aktualnym środowisku. | |||
Jednak poprzednio zdefiniowana stała nie jest usuwana ze środowiska. | |||
Jak zobaczymy, będzie to miało znaczenie przy obliczaniu procedur odwołujących się do wcześniej zdefiniowanych stałych. | |||
</p> | |||
{{przyklad|[Przysłanianie definicji stałych w środowisku]||}} | |||
[[ | [[Image:pf-rys-3-1.gif||center]] | ||
<br/><center>[[/Przesyłanie definicji stałych w środowisku|Zobacz animację]]</center><br/> | |||
Ramka może zawierać więcej niż jedną | <p align="justify"> | ||
Ramka może zawierać więcej niż jedną stałą, jeżeli w definicji użyjemy spójnika <tt>and</tt>. | |||
</p> | |||
[ | {{przyklad|[Przysłanianie definicji stałych i definicje równoczesne]||}} | ||
[[Image:pf-rys-3-2.gif||center]] | |||
<br/><center>[[/Przysłanianie definicji stałych i definicje równoczesne|Zobacz animację]]</center><br/> | |||
== Wartości typów danych == | |||
<p align="justify"> | |||
Wartości prostych typów wbudowanych (takie jak <tt>int</tt>, <tt>bool</tt>, czy <tt>float</tt>) są pamiętane w ramkach wprost. | |||
Wartości typów złożonych są pamiętane jako wskaźniki do odpowiednich struktur wskaźnikowych reprezentujących te wartości. Dzięki przyjęciu takiej konwencji, reprezentacja dowolnej wartości zajmuje zawsze stałą pamięć. | |||
(Dotyczy to zarówno wartości przechowywanych w ramkach, jak i przekazywanych obliczanych wartości wyrażeń.) | |||
W rezultacie definiując stałe o złożonych wartościach nie kopiujemy tych wartości, a jedynie wskaźniki do nich. | |||
Dodatkowo, ponieważ raz powstałe wartości nie ulegają zmianie, struktury danych reprezentujące różne wartości mogą współdzielić pewne fragmenty. | |||
</p> | |||
<p align="justify"> | |||
Wartości różnych złożonych typów danych są generalnie reprezentowane jako rekordy złożone ze wskaźników do wartości składowych: | |||
* Element produktu kartezjańskiego jest reprezentowany jako n-tka wskaźników do tworzących go wartości współrzędnych. | |||
* Rekord -- podobnie jak produkt kartezjański jest reprezentowany jako rekordy złożony z wskaźników do wartości pól. | |||
* Warianty bez argumentów są pamiętane jako stałe wyznaczające operator, a warianty z argumentami są pamiętane jako pary: stała wyznaczająca operator i wskaźnik do argumentu. | |||
* Lista pusta jest reprezentowana jako stała, a lista niepusta jest reprezentowana jako para: głowa i ogon. | |||
</p> | |||
{{przyklad|[Wartości złożonych typów danych -- <math>n</math>-tki]||}} | |||
[[Image:Pf-rys-3-b.png||center]] | |||
<br/><center>[[/Wartości złożonych typów danych - n-tki|Zobacz animację]]</center><br/> | |||
{{przyklad|[Wartości złożonych typów danych -- listy]||}} | |||
[[Image:Pf-rys-3-c.png||center]] | |||
<br/><center>[[/Wartości złożonych typów danych - listy|Zobacz animację]]</center><br/> | |||
== Wartości proceduralne == | |||
<p align="justify"> | |||
Na wartość procedury składają sie trzy elementy: | Na wartość procedury składają sie trzy elementy: | ||
nazwy | * nazwy parametrów formalnych procedury, | ||
* treść procedury i | |||
* wskaźnik do środowiska, w którym zdefiniowano procedurę. | |||
Pierwsze dwa elementy przekładają się w trakcie kompilacji na kod procedury. | |||
Natomiast wskaźnik do środowiska, w którym zdefiniowano procedurę, może być ustalony dopiero w trakcie obliczeń -- | |||
dotyczy to np. procedur lokalnych. | |||
Reasumując, wartość procedury jest reprezentowana jako para wskaźników: do kodu skompilowanej procedury i do środowiska, w którym procedura została zdefiniowana. | |||
W przypadku procedur rekurencyjnych "środowisko, w którym zdefiniowano procedurę" zawiera jej własną definicję. | |||
</p> | |||
{{uwaga||uwaga_args| Formalnie rzecz biorąc, jak zobaczymy dalej, każda procedura ma tylko jden argument. Dopóki jednak nie dowiemy się dlaczego tak jest i nie wprowadzimy procedur wyższych rzędów, oraz w sytuacjach, gdy takie uproszczenie nie będzie prowadzić do nieporozumień, będziemy dopuszczać obiekty proceduralne z wieloma argumentami. Uproszczenie takie jest możliwe wtedy, gdy w zastosowaniach procedury wszystkie jej parametry otrzymują wartości.}} | |||
=== Zastosowanie procedury do argumentów === | |||
<p align="justify"> | |||
Zastosowanie procedury, czyli obliczenie jej wartości, polega na: | |||
* | * wyliczeniu wartości wszystkich potrzebnych elementów: procedury i jej argumentów, | ||
* stworzeniu nowej ramki, dla której środowiskiem otaczającym jest środowisko, w którym zdefiniowano procedurę, a nazwom parametrów formalnych przyporządkowano wartości argumentów, | |||
* wyliczeniu w takim środowisku wartości wyrażenia stanowiącego treść procedury. | |||
* | </p> | ||
{{przyklad|[Zastosowanie procedury nazwanej]||}} | |||
Wprowadzenie definicji: | |||
'''let''' x = 2;; | '''let''' x = 2;; | ||
| Linia 70: | Linia 119: | ||
'''let''' pitagoras x y = square x + square y;; | '''let''' pitagoras x y = square x + square y;; | ||
[[ | powoduje następujace rozszerzenie środowiska: | ||
{{przyklad|[Definicje procedur globalnych]||}} | |||
[[Image:pf-rys-3-3.gif||center]] | |||
<br/><center>[[/Definicje procedur globalnych|Zobacz animację]]</center><br/> | |||
Obliczenie wyrażenia: | Obliczenie wyrażenia: | ||
pitagoras x (x + 1) + pitagoras x ((square x) + 1);; | pitagoras x (x + 1) + pitagoras x ((square x) + 1);; | ||
[[ | przebiega następująco: | ||
{{przyklad|[Zastosowanie procedur nazwanych]||}} | |||
[[Image:pf-rys-3-4.gif||center]] | |||
<br/><center>[[/Zastosowanie procedur nazwanych|Zobacz animację]]</center><br/> | |||
Prześledźmy obliczenie prostego wyrażenia zawierającego <math>\lambda</math>-abstrakcję: | |||
{{przyklad|[Zastosowanie <math>\lambda</math>-abstrakcji]||}} | |||
[[Image:pf-rys-3-5.gif||center]] | |||
< | <br/><center>[[/Zastosowanie lambda-abstrakcji|Zobacz animację]]</center><br/> | ||
[ | {{przyklad|[Zastosowanie procedury rekurencyjnej]||}} | ||
let '''rec''' silnia n = | let '''rec''' silnia n = | ||
'''if''' n < 2 '''then''' 1 '''else''' n * silnia (n - 1);; | '''if''' n < 2 '''then''' 1 '''else''' n * silnia (n - 1);; | ||
silnia 3;; | silnia 3;; | ||
[[Image:pf-rys-3-6.gif||center]] | |||
<br/><center>[[/Zastosowanie procedury rekurencyjnej|Zobacz animację]]</center><br/> | |||
Jeśli wartości zwracane przez wszystkie wywołania rekurencyjne, bez żadnego przetwarzania są przekazywane jako wynik danej procedury, to mówimy o rekurencji ogonowej. W przypadku rekurencji ogonowej, w momencie wywołania rekurencyjnego nie musimy tworzyć nowej ramki --- możemy wykorzystać istniejącą ramkę zmieniając jedynie wartości argumentów. | == Rekurencja ogonowa == | ||
<p align="justify"> | |||
Jeśli wartości zwracane przez wszystkie wywołania rekurencyjne, bez żadnego przetwarzania, są przekazywane jako wynik danej procedury, to mówimy o rekurencji ogonowej. | |||
W przypadku rekurencji ogonowej, w momencie wywołania rekurencyjnego nie musimy tworzyć nowej ramki --- | |||
możemy wykorzystać istniejącą ramkę, zmieniając jedynie pamiętane w niej wartości argumentów. | |||
W przypadku rekurencji ogonowej koszt pamięciowy związany z ramkami dla kolejnych wywołań rekurencyjnych jest stały, gdyż jest to tylko jedna ramka. | |||
</p> | |||
{{przyklad|[Rekurencja ogonowa -- silnia]||}} | |||
<p align="justify"> | |||
Oto procedura obliczająca silnię z rekurencją ogonową. | |||
Zwróćmy uwagę na dodatkowy parametr <tt>a</tt>, w którym kumuluje się wynik. | |||
Takie dodatkowe parametry są nazywane ''akumulatorami''. | |||
Dzięki zastosowaniu akumulatora mamy rekurencję ogonową. | |||
</p> | |||
'''let''' '''rec''' s a x = | '''let''' '''rec''' s a x = | ||
'''if''' x <= 1 '''then''' a '''else''' s (a * x) (x - 1);; | '''if''' x <= 1 '''then''' a '''else''' s (a * x) (x - 1);; | ||
'''let''' silnia x = s 1 x;; | '''let''' silnia x = s 1 x;; | ||
silnia 3;; | silnia 3;; | ||
[[Image:pf-rys-3-7.gif||center]] | |||
<br/><center>[[/Rekurencja ogonowa - silnia|Zobacz animację]]</center><br/> | |||
{{przyklad|[Rekurencja ogonowa -- liczby Fibonacciego]||}} | |||
<p align="justify"> | |||
Oto procedura obliczająca liczby Fibonacciego z rekurencją ogonową i akumulatorem. | |||
</p> | |||
'''let''' '''rec''' fibpom a b n = | '''let''' '''rec''' fibpom a b n = | ||
'''if''' n = 0 '''then''' a '''else''' fibpom b (a + b) (n - 1);; | '''if''' n = 0 '''then''' a '''else''' fibpom b (a + b) (n - 1);; | ||
| Linia 118: | Linia 191: | ||
fib 5;; | fib 5;; | ||
[[ | [[Image:pf-rys-3-8.gif||center]] | ||
<br/><center>[[/Rekurencja ogonowa - liczby Fibonacciego|Zobacz animację]]</center><br/> | |||
== Definicje lokalne == | |||
<p align="justify"> | |||
Mówiliśmy wcześniej, że wyrażenie postaci: | |||
</p> | |||
'''let''' <math>a</math> = <math>b</math> '''in''' <math>c</math> | '''let''' <math>a</math> = <math>b</math> '''in''' <math>c</math> | ||
jest | <p align="justify"> | ||
jest podobne do zastosowania <math>\lambda</math>-abstrakcji postaci: | |||
</p> | |||
('''function''' <math>a</math> -> <math>c</math>) <math>b</math> | ('''function''' <math>a</math> -> <math>c</math>) <math>b</math> | ||
<p align="justify"> | |||
Sposób obliczania wyrażenia <tt>let ... in ...</tt> jest analogiczny do sposobu obliczania takiej <math>\lambda</math>-abstrakcji: | |||
* tworzona jest ramka zawierająca definicję symboli lokalnych (otaczającym ją środowiskiem jest aktualne środowisko), | * tworzona jest ramka zawierająca definicję symboli lokalnych (otaczającym ją środowiskiem jest aktualne środowisko), | ||
* w tak powstałym środowisku wyliczana jest wartość wyrażenia, | * w tak powstałym środowisku wyliczana jest wartość wyrażenia stojącego po <tt>in</tt>, | ||
* po czym | * po czym przywracane jest aktualne środowisko sprzed obliczenia całego wyrażenia. | ||
Jeżeli definicje lokalne są pozagnieżdżane, to powstaje odpowiednio więcej ramek z wartościami symboli lokalnych. | |||
</p> | |||
{{przyklad|[Zagnieżdżone definicje lokalne]||}} | |||
Następujący przykład pokazuje sposób | Następujący przykład pokazuje sposób obliczania definicji lokalnych. | ||
lokalnych. | |||
'''let''' f x = | '''let''' f x = | ||
| Linia 147: | Linia 225: | ||
x + y + z;; | x + y + z;; | ||
f 9;; | f 9;; | ||
[[Image:pf-rys-3-9.gif||center]] | |||
<br/><center>[[/Zagnieżdżone definicje lokalne|Zobacz animację]]</center><br/> | |||
{{przyklad|[Procedury lokalne]||}} | |||
Niniejszy przykład ilustruje mniej typową kombinację użycia definicji lokalnych i procedur. | Niniejszy przykład ilustruje mniej typową kombinację użycia definicji lokalnych i procedur. | ||
| Linia 159: | Linia 238: | ||
'''let''' h x = f (x * x);; | '''let''' h x = f (x * x);; | ||
h 5;; | h 5;; | ||
[[ | <p align="justify"> | ||
Zwróćmy uwagę na procedurę pomocniczą <tt>g</tt>. | |||
Procedura ta jest widoczna tylko wewnątrz procedury <tt>f</tt>, a jednak jej definicja ma tylko jedną instancję. | |||
</p> | |||
[[Image:pf-rys-3-10.gif||center]] | |||
<br/><center>[[/Procedury lokalne 1|Zobacz animację]]</center><br/> | |||
{{przyklad|[Procedury lokalne]||}} | |||
'''let''' f x y = | '''let''' f x y = | ||
| Linia 172: | Linia 255: | ||
g x + g y;; | g x + g y;; | ||
f 4 2 - f 2 1;; | f 4 2 - f 2 1;; | ||
<p align="justify"> | |||
W tym przykładzie, w każdym wywołaniu procedury <tt>f</tt>powstaje osobna instancja procedury lokalnej <tt>g</tt>. | |||
Jest to naturalne zważywszy, że procedura <tt>g</tt> korzysta z argumentów wywołania procedury <tt>f</tt>. | |||
</p> | |||
[[Image:pf-rys-3-11.gif||center]] | |||
<br/><center>[[/Procedury lokalne 2|Zobacz animację]]</center><br/> | |||
== Ramki a rekordy aktywacji == | |||
<p align="justify"> | |||
Ramkom odpowiadają w językach imperatywnych ''rekordy aktywacji''. | |||
Rekord aktywacji to porcja informacji towarzysząca pojedynczemu wywołaniu procedury. | |||
W rekordach aktywacji pamiętane są np. wartości zmiennych lokalnych. | |||
Rekordy aktywacji są pamiętane na stosie. | |||
W momencie powrotu z wywołania procedury, związany z nim rekord aktywacji jest niszczony. | |||
</p> | |||
<p align="justify"> | |||
Pokażemy na przykładach, że w naszym modelu obliczeniowym tak nie jest. | |||
Wynika to z funkcyjnego charakteru języka oraz z tego, że procedury mogą być wynikami procedur. | |||
Ramka, zawierająca lokalne definicje lub argumenty procedury, nie musi stawać się od razu zbędna, | |||
gdyż mogą na nią wskazywać wartości proceduralne. | |||
Jesli spojrzymy na wszystkie ramki, to nie tworzą one listy ani stosu, ale drzewo | |||
(wskaźniki na otaczające środowisko prowadzą w górę tego drzewa). | |||
Ramki, które trzeba trzymać w pamięci, bo są potrzebne też nie muszą tworzyć listy, tylko drzewo. | |||
Zjawisko to występuje np. wówczas, gdy wynikiem procedury jest procedura mająca dostęp do lokalnie zdefiniowanych symboli. | |||
</p> | |||
{{przyklad|[Procedura lokalna jako wynik]|| | |||
Niniejszy przykład pokazuje sytuację, gdy ramki powstałe w czasie wywołania procedury mogą być potrzebne po jego zakończeniu. | Niniejszy przykład pokazuje sytuację, gdy ramki powstałe w czasie wywołania procedury mogą być potrzebne po jego zakończeniu.}} | ||
'''let''' f x = | '''let''' f x = | ||
| Linia 192: | Linia 293: | ||
h 7;; | h 7;; | ||
[[ | [[Image:pf-rys-3-12.gif||center]] | ||
<br/><center>[[/Procedura lokalna jako wynik|Zobacz animację]]</center><br/> | |||
Ramka zawierająca definicję procedury <tt>g</tt> powstaje w wyniku wywołania <tt>f 6</tt>, ale jest potrzebna później, do obliczenia <tt>h 7</tt>. | |||
{{przyklad|[Przekazywanie wielu argumentów]|| | |||
Poniższy przykład ilustruje sposób przekazywania do procedury wielu argumentów, tak jak to jest realizowane --- po jednym na raz.}} | |||
Poniższy przykład ilustruje sposób przekazywania wielu argumentów, tak jak to jest realizowane --- po jednym na raz. | |||
'''let''' g x = | '''let''' g x = | ||
| Linia 207: | Linia 309: | ||
h 6;; | h 6;; | ||
[[ | [[Image:pf-rys-3-13.gif||center]] | ||
<br/><center>[[/Przekazywanie wielu argumentów|Zobacz animację]]</center><br/> | |||
== Odśmiecanie == | |||
<p align="justify"> | |||
W przedstwaionym modelu obliczeń cały czas są tworzone ramki i elementy struktur danych. | |||
Co więcej, jak widzieliśmy, nie możemy usuwać ramek powstałych na potrzeby definicji lokalnych i | |||
zastosować procedur po obliczeniu wyników, gdyż mogą one być nadal potrzebne. | |||
Gdy brakuje wolnej pamięci, uruchamiany jest proces ''odśmiecania''. | |||
Proces ten usuwa wszystkie te ramki i elementy struktur danych, które nie są dostępne i tym samym nie mogą być już do niczego potrzebne. | |||
</p> | |||
<p align="justify"> | |||
W tym celu przeszukuje się strukturę wskaźnikową ramek i danych. | |||
Za punkt wyjścia służą wszystkie te środowiska, w kontekście których są aktualnie obliczane wyrażenia, plus aktualne środowisko globalne. | |||
Wszystkie te ramki i rekordy, które są z nich dostępne (pośrednio lub bezpośrednio) są potrzebne. | |||
Natomiast te, które są niedostępne, mogą być usunięte. | |||
</p> | |||
<p align="justify"> | |||
Obliczając złożoność czasową programów możemy pominąć koszt odśmiecania. | |||
Zwykle odśmiecanie jest tak zrealizowane, że jego koszt zamortyzowany jest stały. | |||
Można go wliczyć w koszt czasowy tworzenia nowych ramek i rekordów, obciążając utworzenie każdej ramki i rekordu stałym kosztem czasowym. | |||
</p> | |||
<p align="justify"> | |||
Obliczanie kosztu pamięciowego jest skomplikowane. | |||
Należy prześledzić plątaninę powstających ramek i rekordów, | |||
sprawdzić które są w danym momencie niezbędne, a które mogą zostać odśmiecone i | |||
określić minimalną wielkość pamięci niezbędnej do przeprowadzenia obliczeń. | |||
Dodatkowo możemy przyjąć konwencję, że rozmiar danych nie wlicza się do złożoności pamięciowej. | |||
Wynika to z charakteru programowania funkcyjnego. | |||
Przekazane dane nie mogą być modyfikowane przez program. | |||
</p> | |||
== Deser == | |||
[[Image:pf-rys-xkcd-1270.png||center]] | |||
[[http://xkcd.com/1270/ http://xkcd.com/1270/]] | |||
== Ćwiczenia == | |||
[[Programowanie funkcyjne/Model obliczeń/Ćwiczenia |Ćwiczenia]] | |||
Aktualna wersja na dzień 16:06, 5 sty 2014
Wstęp
W tym wykładzie przedstawimy uproszczoną semantykę operacyjną poznanego fragmentu Ocamla. Z jednej strony będzie to model wykonywania obliczeń na tyle dokładny, że pozwoli nam określić wyniki oraz złożoność czasową i pamięciową obliczeń. Z drugiej strony będzie on uproszczony, gdyż pewne kwestie pominiemy, np. kontrolę typów, rozmaite optymalizacje wykonywane przez kompilator, czy sposób realizacji tych elementów języka, których jeszcze nie poznaliśmy. Wyjaśnimy też pewne szczegóły wykonywania obliczeń, które pominęliśmy wcześniej.
Środowisko i ramki
Przedstawiając podstawy Ocamla mówiliśmy o środowisku przypisującym nazwom stałe ich wartości. Dodatkowo takich środowisk może być wiele: środowisko zawierające wszystkie aktualnie globalnie zdefiniowane stałe, środowiska powstające na potrzeby definicji lokalnych i wywołań procedur.
Środowisko jest zrealizowane jako lista jednokierunkowa, tzw. lista ramek. Każda ramka zawiera identyfikator (lub identyfikatory) i ich wartości (lub wskaźniki do takich wartości) oraz wskaźnik do kolejnej ramki tworzącej środowisko. Poszukując w środowisku wartości stałej, przeglądamy kolejne ramki środowiska. Pierwsza ramka, która zawiera nazwę stałej, określa jej wartość.
Dalej będziemy utożsamiać środowisko ze wskaźnikiem do pierwszej ramki tworzącej środowisko. Środowisko reprezentowane przez listę ramek bez pierwszej ramki będziemy nazywać środowiskiem otaczającym, a wskaźnik prowadzący z jednej ramki do kolejnej będziemy nazywać wskaźnikiem do środowiska otaczającego.
Przykład [Dodawanie ramek do środowiska]

Definicje globalne
Prowadząc interakcję z kompilatorem, pracujemy w kontekście tzw. aktualnego środowiska (globalnego). Każda dodana definicja zmienia to środowisko. Zdefiniowanie nowych wartości powoduje dodanie nowej ramki zawierającej zdefiniowane wartości. Dotychczasowe środowisko staje się środowiskiem otaczającym tej ramki. Utworzona ramka staje się nowym aktualnym środowiskiem (globalnym).
Mechanizm ten pozwala na przesłanianie istniejących w środowisku stałych. Jeśli zdefiniujemy nową stałą o takiej samej nazwie, to będzie ona znajdowała się we wcześniejszej ramce i to właśnie ona będzie znajdowana w aktualnym środowisku. Jednak poprzednio zdefiniowana stała nie jest usuwana ze środowiska. Jak zobaczymy, będzie to miało znaczenie przy obliczaniu procedur odwołujących się do wcześniej zdefiniowanych stałych.
Przykład [Przysłanianie definicji stałych w środowisku]
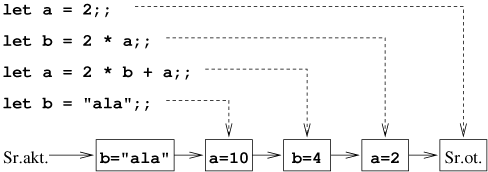
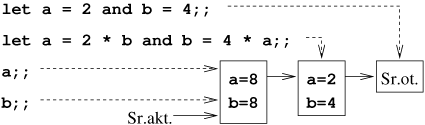
Ramka może zawierać więcej niż jedną stałą, jeżeli w definicji użyjemy spójnika and.
Przykład [Przysłanianie definicji stałych i definicje równoczesne]
Wartości typów danych
Wartości prostych typów wbudowanych (takie jak int, bool, czy float) są pamiętane w ramkach wprost. Wartości typów złożonych są pamiętane jako wskaźniki do odpowiednich struktur wskaźnikowych reprezentujących te wartości. Dzięki przyjęciu takiej konwencji, reprezentacja dowolnej wartości zajmuje zawsze stałą pamięć. (Dotyczy to zarówno wartości przechowywanych w ramkach, jak i przekazywanych obliczanych wartości wyrażeń.) W rezultacie definiując stałe o złożonych wartościach nie kopiujemy tych wartości, a jedynie wskaźniki do nich. Dodatkowo, ponieważ raz powstałe wartości nie ulegają zmianie, struktury danych reprezentujące różne wartości mogą współdzielić pewne fragmenty.
Wartości różnych złożonych typów danych są generalnie reprezentowane jako rekordy złożone ze wskaźników do wartości składowych:
- Element produktu kartezjańskiego jest reprezentowany jako n-tka wskaźników do tworzących go wartości współrzędnych.
- Rekord -- podobnie jak produkt kartezjański jest reprezentowany jako rekordy złożony z wskaźników do wartości pól.
- Warianty bez argumentów są pamiętane jako stałe wyznaczające operator, a warianty z argumentami są pamiętane jako pary: stała wyznaczająca operator i wskaźnik do argumentu.
- Lista pusta jest reprezentowana jako stała, a lista niepusta jest reprezentowana jako para: głowa i ogon.
Przykład [Wartości złożonych typów danych -- -tki]

Przykład [Wartości złożonych typów danych -- listy]
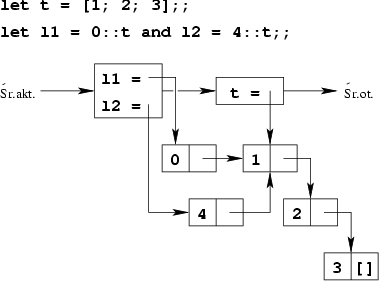
Wartości proceduralne
Na wartość procedury składają sie trzy elementy:
- nazwy parametrów formalnych procedury,
- treść procedury i
- wskaźnik do środowiska, w którym zdefiniowano procedurę.
Pierwsze dwa elementy przekładają się w trakcie kompilacji na kod procedury. Natomiast wskaźnik do środowiska, w którym zdefiniowano procedurę, może być ustalony dopiero w trakcie obliczeń -- dotyczy to np. procedur lokalnych. Reasumując, wartość procedury jest reprezentowana jako para wskaźników: do kodu skompilowanej procedury i do środowiska, w którym procedura została zdefiniowana. W przypadku procedur rekurencyjnych "środowisko, w którym zdefiniowano procedurę" zawiera jej własną definicję.
Zastosowanie procedury do argumentów
Zastosowanie procedury, czyli obliczenie jej wartości, polega na:
- wyliczeniu wartości wszystkich potrzebnych elementów: procedury i jej argumentów,
- stworzeniu nowej ramki, dla której środowiskiem otaczającym jest środowisko, w którym zdefiniowano procedurę, a nazwom parametrów formalnych przyporządkowano wartości argumentów,
- wyliczeniu w takim środowisku wartości wyrażenia stanowiącego treść procedury.
Przykład [Zastosowanie procedury nazwanej]
Wprowadzenie definicji:
let x = 2;; let square x = x * x;; let pitagoras x y = square x + square y;;
powoduje następujace rozszerzenie środowiska:
Przykład [Definicje procedur globalnych]
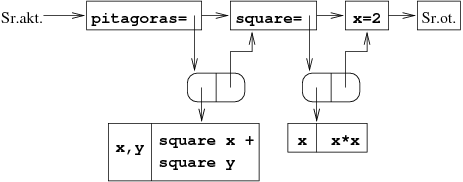
Obliczenie wyrażenia:
pitagoras x (x + 1) + pitagoras x ((square x) + 1);;
przebiega następująco:
Przykład [Zastosowanie procedur nazwanych]
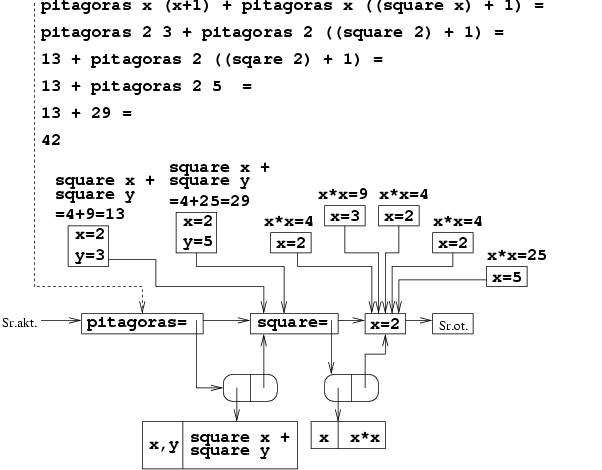
Prześledźmy obliczenie prostego wyrażenia zawierającego -abstrakcję:
Przykład [Zastosowanie -abstrakcji]
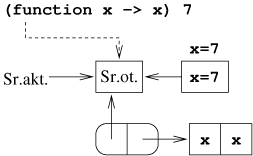
Przykład [Zastosowanie procedury rekurencyjnej]
let rec silnia n = if n < 2 then 1 else n * silnia (n - 1);; silnia 3;;

Rekurencja ogonowa
Jeśli wartości zwracane przez wszystkie wywołania rekurencyjne, bez żadnego przetwarzania, są przekazywane jako wynik danej procedury, to mówimy o rekurencji ogonowej. W przypadku rekurencji ogonowej, w momencie wywołania rekurencyjnego nie musimy tworzyć nowej ramki --- możemy wykorzystać istniejącą ramkę, zmieniając jedynie pamiętane w niej wartości argumentów. W przypadku rekurencji ogonowej koszt pamięciowy związany z ramkami dla kolejnych wywołań rekurencyjnych jest stały, gdyż jest to tylko jedna ramka.
Przykład [Rekurencja ogonowa -- silnia]
Oto procedura obliczająca silnię z rekurencją ogonową. Zwróćmy uwagę na dodatkowy parametr a, w którym kumuluje się wynik. Takie dodatkowe parametry są nazywane akumulatorami. Dzięki zastosowaniu akumulatora mamy rekurencję ogonową.
let rec s a x = if x <= 1 then a else s (a * x) (x - 1);; let silnia x = s 1 x;; silnia 3;;
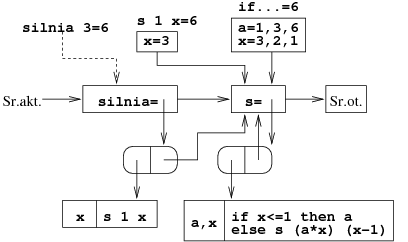
Przykład [Rekurencja ogonowa -- liczby Fibonacciego]
Oto procedura obliczająca liczby Fibonacciego z rekurencją ogonową i akumulatorem.
let rec fibpom a b n =
if n = 0 then a else fibpom b (a + b) (n - 1);;
let fib n = fibpom 0 1 n;;
fib 5;;

Definicje lokalne
Mówiliśmy wcześniej, że wyrażenie postaci:
let = in
jest podobne do zastosowania -abstrakcji postaci:
(function -> )
Sposób obliczania wyrażenia let ... in ... jest analogiczny do sposobu obliczania takiej -abstrakcji:
- tworzona jest ramka zawierająca definicję symboli lokalnych (otaczającym ją środowiskiem jest aktualne środowisko),
- w tak powstałym środowisku wyliczana jest wartość wyrażenia stojącego po in,
- po czym przywracane jest aktualne środowisko sprzed obliczenia całego wyrażenia.
Jeżeli definicje lokalne są pozagnieżdżane, to powstaje odpowiednio więcej ramek z wartościami symboli lokalnych.
Przykład [Zagnieżdżone definicje lokalne]
Następujący przykład pokazuje sposób obliczania definicji lokalnych.
let f x = let y = x + 2 in let z = 2 * y in x + y + z;; f 9;;
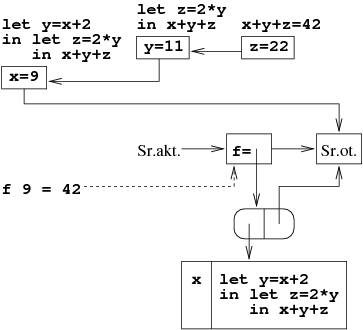
Przykład [Procedury lokalne]
Niniejszy przykład ilustruje mniej typową kombinację użycia definicji lokalnych i procedur.
let f = let g x = x - 8 in fun x -> g (2 * x);; let h x = f (x * x);; h 5;;
Zwróćmy uwagę na procedurę pomocniczą g. Procedura ta jest widoczna tylko wewnątrz procedury f, a jednak jej definicja ma tylko jedną instancję.

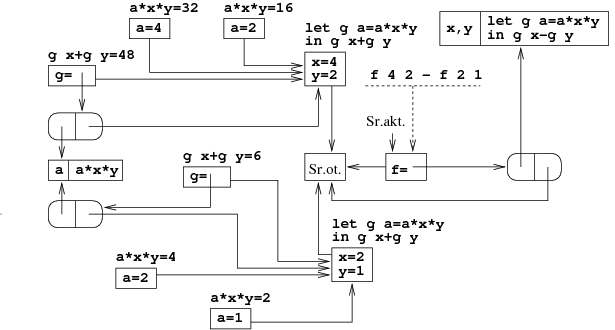
Przykład [Procedury lokalne]
let f x y = let g a = a * x * y in g x + g y;; f 4 2 - f 2 1;;
W tym przykładzie, w każdym wywołaniu procedury fpowstaje osobna instancja procedury lokalnej g. Jest to naturalne zważywszy, że procedura g korzysta z argumentów wywołania procedury f.
Ramki a rekordy aktywacji
Ramkom odpowiadają w językach imperatywnych rekordy aktywacji. Rekord aktywacji to porcja informacji towarzysząca pojedynczemu wywołaniu procedury. W rekordach aktywacji pamiętane są np. wartości zmiennych lokalnych. Rekordy aktywacji są pamiętane na stosie. W momencie powrotu z wywołania procedury, związany z nim rekord aktywacji jest niszczony.
Pokażemy na przykładach, że w naszym modelu obliczeniowym tak nie jest. Wynika to z funkcyjnego charakteru języka oraz z tego, że procedury mogą być wynikami procedur. Ramka, zawierająca lokalne definicje lub argumenty procedury, nie musi stawać się od razu zbędna, gdyż mogą na nią wskazywać wartości proceduralne. Jesli spojrzymy na wszystkie ramki, to nie tworzą one listy ani stosu, ale drzewo (wskaźniki na otaczające środowisko prowadzą w górę tego drzewa). Ramki, które trzeba trzymać w pamięci, bo są potrzebne też nie muszą tworzyć listy, tylko drzewo. Zjawisko to występuje np. wówczas, gdy wynikiem procedury jest procedura mająca dostęp do lokalnie zdefiniowanych symboli.
Przykład [Procedura lokalna jako wynik]
let f x = let g y = x * y in g;; let h = f 6;; h 7;;
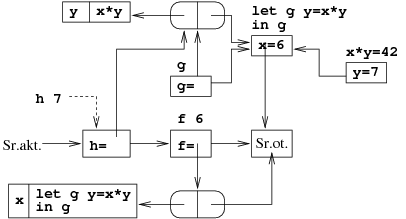
Ramka zawierająca definicję procedury g powstaje w wyniku wywołania f 6, ale jest potrzebna później, do obliczenia h 7.
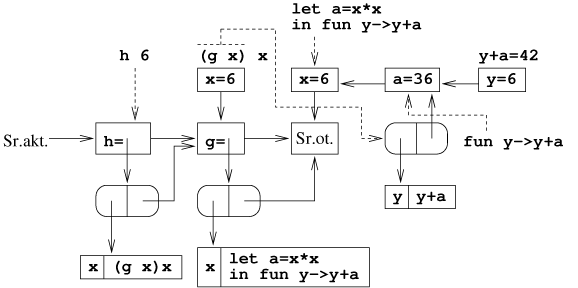
Przykład [Przekazywanie wielu argumentów]
let g x =
let
a = x * x
in
fun y -> y + a;;
let h x = (g x) x;;
h 6;;
Odśmiecanie
W przedstwaionym modelu obliczeń cały czas są tworzone ramki i elementy struktur danych. Co więcej, jak widzieliśmy, nie możemy usuwać ramek powstałych na potrzeby definicji lokalnych i zastosować procedur po obliczeniu wyników, gdyż mogą one być nadal potrzebne. Gdy brakuje wolnej pamięci, uruchamiany jest proces odśmiecania. Proces ten usuwa wszystkie te ramki i elementy struktur danych, które nie są dostępne i tym samym nie mogą być już do niczego potrzebne.
W tym celu przeszukuje się strukturę wskaźnikową ramek i danych. Za punkt wyjścia służą wszystkie te środowiska, w kontekście których są aktualnie obliczane wyrażenia, plus aktualne środowisko globalne. Wszystkie te ramki i rekordy, które są z nich dostępne (pośrednio lub bezpośrednio) są potrzebne. Natomiast te, które są niedostępne, mogą być usunięte.
Obliczając złożoność czasową programów możemy pominąć koszt odśmiecania. Zwykle odśmiecanie jest tak zrealizowane, że jego koszt zamortyzowany jest stały. Można go wliczyć w koszt czasowy tworzenia nowych ramek i rekordów, obciążając utworzenie każdej ramki i rekordu stałym kosztem czasowym.
Obliczanie kosztu pamięciowego jest skomplikowane. Należy prześledzić plątaninę powstających ramek i rekordów, sprawdzić które są w danym momencie niezbędne, a które mogą zostać odśmiecone i określić minimalną wielkość pamięci niezbędnej do przeprowadzenia obliczeń. Dodatkowo możemy przyjąć konwencję, że rozmiar danych nie wlicza się do złożoności pamięciowej. Wynika to z charakteru programowania funkcyjnego. Przekazane dane nie mogą być modyfikowane przez program.
Deser
