Matematyka dyskretna 1/Wykład 2: Rekurencja: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
|||
| (Nie pokazano 41 wersji utworzonych przez 7 użytkowników) | |||
| Linia 1: | Linia 1: | ||
==Definicje rekurencyjne== | =={{kotwica|defrek|Definicje rekurencyjne}}== | ||
Definicja rekurencyjna (indukcyjna): | Definicja rekurencyjna (indukcyjna): | ||
| Linia 15: | Linia 15: | ||
<center><math>n!=n(n-1)\cdot\ldots\cdot2\cdot1 | <center><math>n!=n(n-1)\cdot\ldots\cdot2\cdot1</math></center> | ||
</math></center> | |||
| Linia 35: | Linia 34: | ||
<center><math>\ | <center><math>\begin{align} s_0 &= 1 | ||
\\ | \\ | ||
s_{n} &= | s_{n} &= n \cdot s_{n-1} \quad \text{dla} \quad n\geq 1. | ||
\ | \end{align}</math></center> | ||
| Linia 44: | Linia 43: | ||
<center><math>\ | <center> | ||
<math>\begin{align} s_0 &= 1 | |||
\\ | \\ | ||
s_1 &= | s_1 &= 1 \cdot s_{0} = 1 \cdot 1 = 1 | ||
\\ | \\ | ||
s_2 &= | s_2 &= 2 \cdot s_{1} = 2 \cdot 1 = 2 | ||
\\ | \\ | ||
s_3 &= | s_3 &= 3 \cdot s_{2} = 3 \cdot 2 = 6 | ||
\\ | \\ | ||
s_4 &= | s_4 &= 4 \cdot s_{3} = 4 \cdot 6 = 24 | ||
\\ | \\ | ||
\ldots | \ldots | ||
\ | \end{align}</math> | ||
</center> | |||
| Linia 64: | Linia 65: | ||
<center><math>\ | <center><math>\begin{align} s_0 &= 0 | ||
\\ | \\ | ||
s_{n} &= | s_{n} &= n \cdot s_{n-1}\quad \text{dla}\quad n\geq 1 | ||
\ | \end{align}</math></center> | ||
| Linia 73: | Linia 74: | ||
<center><math>\ | <center><math>\begin{align} s_0 &=\frac{1}{2} | ||
\\ | \\ | ||
s_{n} &= | s_{n} &= n \cdot s_{n-1} \quad \text{dla}\quad n\geq 1 | ||
\ | \end{align}</math></center> | ||
| Linia 82: | Linia 83: | ||
<center><math>\ | <center><math>\begin{align} s_0 &= 1 | ||
\\ | \\ | ||
s_{n} &= | s_{n} &= n \cdot s_{n-2} \quad \text{dla}\quad n\geq 2. | ||
\ | \end{align}</math></center> | ||
| Linia 92: | Linia 93: | ||
W ostatnim przypadku widać, że ponieważ odwołanie jest ''dwa wyrazy wstecz, to już wyliczenie pierwszego wyrazu <math>s_1</math> staje się niemożliwe. | W ostatnim przypadku widać, że ponieważ odwołanie jest ''dwa wyrazy wstecz, to już wyliczenie pierwszego wyrazu <math>s_1</math> staje się niemożliwe. | ||
===Ciąg arytmetyczny=== | ==={{kotwica|carytm|Ciąg arytmetyczny}}=== | ||
{{przyklad||| | {{przyklad||| | ||
| Linia 98: | Linia 99: | ||
<center><math>\ | <center><math>\begin{align} s_0 &= 0 | ||
\\ | \\ | ||
s_{n} &= | s_{n} &= s_{n-1}+2 \quad \text{dla}\quad n\geq 1 | ||
\ | \end{align}</math></center> | ||
| Linia 124: | Linia 125: | ||
<center><math>a_n = a_0 + n\cdot r | <center><math>a_n = a_0 + n\cdot r</math></center> | ||
</math></center> | |||
| Linia 131: | Linia 131: | ||
<center><math>a_0 + 0\cdot r = a_0 \quad\ | <center><math>a_0 + 0\cdot r = a_0 \quad\text{jest rzeczywiście zerowym wyrazem ciągu} | ||
</math></center> | </math></center> | ||
| Linia 141: | Linia 141: | ||
</math></center> | </math></center> | ||
===Ciąg geometryczny=== | ==={{kotwica|cgeo|Ciąg geometryczny}}=== | ||
{{przyklad||| | {{przyklad||| | ||
| Linia 147: | Linia 147: | ||
<center><math>\ | <center><math>\begin{align} s_0 &= 1 | ||
\\ | \\ | ||
s_{n} &= | s_{n} &= 2\cdot s_{n-1} \quad \text{dla}\quad n\geq 1 | ||
\ | \end{align}</math></center> | ||
| Linia 173: | Linia 173: | ||
<center><math>a_n = a_0 \cdot q^n | <center><math>a_n = a_0 \cdot q^n</math></center> | ||
</math></center> | |||
| Linia 180: | Linia 179: | ||
<center><math>a_0 \cdot q^0 = a_0 \cdot 1 = a_0 \quad\ | <center><math>a_0 \cdot q^0 = a_0 \cdot 1 = a_0 \quad\text{jest rzeczywiście zerowym wyrazem ciągu}</math></center> | ||
| Linia 186: | Linia 185: | ||
<center><math>a_0 \cdot q^n = (a_0 \cdot q^{n-1})\cdot q = a_{n-1}\cdot q = a_n | <center><math>a_0 \cdot q^n = (a_0 \cdot q^{n-1})\cdot q = a_{n-1}\cdot q = a_n</math></center> | ||
</math></center> | |||
===Wieże Hanoi=== | ===Wieże Hanoi=== | ||
[[File:Wieza hanoi.mp4|253x253px|thumb|right|Wieża Hanoi]] | |||
{{przyklad|(E.Lucas, 1883)|| | {{przyklad|(E.Lucas, 1883)|| | ||
U zarania czasu Bóg umieścił 64 złote krążki na jednej z trzech diamentowych iglic tak, że krążki wyżej umieszczone miały mniejsze promienie. | U zarania czasu Bóg umieścił 64 złote krążki na jednej z trzech diamentowych iglic tak, że krążki wyżej umieszczone miały mniejsze promienie. | ||
Następnie Bóg polecił grupie mnichów przełożenie tych krążków na trzecią iglicę <math>(C)</math>, ale tak by: | Następnie Bóg polecił grupie mnichów przełożenie tych krążków na trzecią iglicę <math>(C)</math>, ale tak by: | ||
| Linia 211: | Linia 209: | ||
By obliczyć ilość potrzebnych do wykonania ruchów, przeanalizujmy najpierw małe przypadki:<br> | By obliczyć ilość potrzebnych do wykonania ruchów, przeanalizujmy najpierw małe przypadki:<br> | ||
Łatwo zauważyć, że dla 1 krążka potrzebny jest jeden ruch: <math>A\rightarrow C</math><br> | Łatwo zauważyć, że dla 1 krążka potrzebny jest jeden ruch: <math>A\rightarrow C</math><br> | ||
Podobnie dla dwu krążków możemy postąpić: <math>A\rightarrow B, \ \ A\rightarrow C, \ \ B\rightarrow C</math><br> | Podobnie dla dwu krążków możemy postąpić: <math>A \rightarrow B, \ \ A \rightarrow C, \ \ B \rightarrow C</math><br> | ||
Przy 3 krążkach postępujemy tak: | Przy 3 krążkach postępujemy tak: | ||
* najpierw przenosimy dwa górne krążki na iglicę <math>B</math> posługując się iglicą <math>C</math>: | * najpierw przenosimy dwa górne krążki na iglicę <math>B</math> posługując się iglicą <math>C</math>: | ||
<center><math>A\rightarrow C, \ \ A\rightarrow B, \ \ C\rightarrow B | <center><math>A \rightarrow C, \ \ A \rightarrow B, \ \ C \rightarrow B</math></center> | ||
</math></center> | |||
* przenosimy największy krążek z <math>A</math> na <math>C</math>: | * przenosimy największy krążek z <math>A</math> na <math>C</math>: | ||
| Linia 234: | Linia 231: | ||
<center><math>\ | <center><math>\begin{align} H_1 &= 1 | ||
\\ | \\ | ||
H_2 &= | H_2 &=3 | ||
\\ | \\ | ||
H_3 &= | H_3 &=7 | ||
\ | \end{align}</math></center> | ||
| Linia 262: | Linia 259: | ||
<center><math>\ | <center><math>\begin{align} H_1 &= 1 | ||
\\ | \\ | ||
H_{n} &= | H_{n} &= 2\cdot H_{n-1}+1 \quad \text{dla}\quad n\geq 2 | ||
\ | \end{align}</math></center> | ||
| Linia 295: | Linia 292: | ||
<center><math>\ | <center><math>\begin{align} a_0&=2,\\ | ||
a_{n+1}&= | a_{n+1}&=a_n^2. | ||
\ | \end{align}</math></center> | ||
| Linia 304: | Linia 301: | ||
<center><math>a_n = a_{n-1}^2=a_{n-2}^4=a_{n-3}^8= \ldots =a_0^{2^n}=2^{2^n} | <center><math>a_n = a_{n-1}^2=a_{n-2}^4=a_{n-3}^8= \ldots =a_0^{2^n}=2^{2^n}</math></center> | ||
</math></center> | |||
</div></div> | </div></div> | ||
}} | }} | ||
[[File:MD1-1.5.mp4|250x250px|thumb|right|MD1-1.5.swf]] | |||
{{przyklad||| | {{przyklad||| | ||
| Linia 325: | Linia 323: | ||
* Dla trzech prostych jest to <math>7</math>. | * Dla trzech prostych jest to <math>7</math>. | ||
Zauważmy, że nowa prosta zwiększa ilość obszarów o <math>k</math> jeśli | Zauważmy, że nowa prosta zwiększa ilość obszarów o <math>k</math> jeśli | ||
przecina dokładnie <math>k-1</math> z poprzednich prostych i to w nowych punktach przecięć. Z drugiej strony dwie proste mogą się przeciąć w co najwyżej jednym punkcie i przecinają się o ile nie są równolegle. Widzimy zatem, że najwięcej obszarów dostaniemy kładąc kolejne proste w ten sposób aby żadne dwie nie były równoległe i żadne trzy nie przecinały się w jednym punkcie. Otrzymujemy następujące równanie rekurencyjne: | przecina dokładnie <math>k-1</math> z poprzednich prostych i to w nowych punktach przecięć. Z drugiej strony dwie proste mogą się przeciąć w co najwyżej jednym punkcie i przecinają się o ile nie są równolegle. Widzimy zatem, że najwięcej obszarów dostaniemy kładąc kolejne proste w ten sposób aby żadne dwie nie były równoległe i żadne trzy nie przecinały się w jednym punkcie. Otrzymujemy następujące równanie rekurencyjne: | ||
<center> | |||
<center><math>\ | <math>\begin{align} l_0&=1,\\ | ||
l_{n+1}&= | l_{n+1}&=l_n+n. | ||
\ | \end{align}</math> | ||
</center> | |||
Ponownie rozwiążemy równanie rozwijając je: | Ponownie rozwiążemy równanie rozwijając je: | ||
<center> | |||
<center><math>\ | <math>\begin{align} l_n&=l_{n-1}+n=l_{n-2}+(n-1)+n=l_{n-3}+(n-2)+(n-1)+n=\ldots\\ | ||
&= | &=l_0+1+2+\ldots+n=1+\frac{n(n+1)}{2}, | ||
\ | \end{align}</math> | ||
</center> | |||
gdzie ostatnia równość wynika z - już udowodnionego - wzoru na sumę kolejnych liczb naturalnych. | gdzie ostatnia równość wynika z - już udowodnionego - wzoru na sumę kolejnych liczb naturalnych. | ||
| Linia 350: | Linia 346: | ||
==Liczby Fibonacciego== | ==Liczby Fibonacciego== | ||
[[ | [[grafika:Fibonacci1.jpg|thumb|right||Leonardo Fibonacci (1175-1250)<br>[[Biografia Fibonacci|Zobacz biografię]]]] | ||
Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest | Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest | ||
'''ciąg Fibonacciego''' <math>{\left\{ {f_i} \right\}\ }_{i\in\mathbb{N}}</math> zadany przez | {{kotwica|cfibo|'''ciąg Fibonacciego'''}} <math>{\left\{ {f_i} \right\}\ }_{i\in\mathbb{N}}</math> zadany przez | ||
<center><math>\ | <center> | ||
f_1&= | <math>\begin{align} f_0&=0,\\ | ||
f_{n+2}&= | f_1&=1,\\ | ||
\ | f_{n+2}&=f_n+f_{n+1}. | ||
\end{align}</math> | |||
</center> | |||
| Linia 365: | Linia 363: | ||
<center><math>\begin{array} { | <center> | ||
<math>\begin{array} {c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} | |||
n&0&1&2&3&4&5&6&7&8&9&10&11&12&13&14\\ | n&0&1&2&3&4&5&6&7&8&9&10&11&12&13&14\\ | ||
\hline | \hline | ||
0&1&1&2&3&5&8&13&21&34&55&89&144&233&377&610 | 0&1&1&2&3&5&8&13&21&34&55&89&144&233&377&610\\ | ||
\ | |||
\end{array} | \end{array} | ||
</math></center> | </math> | ||
</center> | |||
| Linia 382: | Linia 380: | ||
Pierwsze pytanie - póki co - wydaje się dość beznadziejne. | Pierwsze pytanie - póki co - wydaje się dość beznadziejne. | ||
[[File:Domino-1.6-1.8.mp4|250x250px|thumb|right|Domino-1.6-1.8.swf]] | |||
{{przyklad||| | {{przyklad||| | ||
Na ile sposobów można ułożyć domina na prostokącie o rozmiarze <math>2 \times n</math>? | Na ile sposobów można ułożyć domina na prostokącie o rozmiarze <math>2 \times n</math>? | ||
<center> | |||
<math>\begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} | |||
\hline | |||
&&&&&&&&&&&&&&&&&&&&&&&&&&&\\ | |||
\hline | |||
&&&&&&&&&&&&&&&&&&&&&&&&&&&\\ | |||
\hline | |||
\end{array} | |||
</math> | |||
</center> | |||
Oznaczmy, tę liczbę przez <math>d_n</math> w zależności od <math>n</math>. | Oznaczmy, tę liczbę przez <math>d_n</math> w zależności od <math>n</math>. | ||
* Dla <math>n=1</math> jest to możliwe na dokładnie jeden sposób, tzn. <math>d_1=1</math> | * Dla <math>n=1</math> jest to możliwe na dokładnie jeden sposób, tzn. <math>d_1=1</math> | ||
* Dla <math>n=2</math> są już dwa takie sposoby:<br> | * Dla <math>n=2</math> są już dwa takie sposoby:<br> | ||
- ustawiamy obie kostki poziomo, lub obie pionowo,<br> | - ustawiamy obie kostki poziomo, lub obie pionowo,<br> | ||
a zatem <math>d_2=2</math>. | a zatem <math>d_2=2</math>. | ||
* Dla <math>n=3</math> są trzy sposoby, | * Dla <math>n=3</math> są trzy sposoby, | ||
* Pokrywając większy prostokąt <math>2 \times n</math> musimy jakoś pokryć dwa skrajne pola przylegające do krótszej krawędzi o długości <math>2</math>. Można to zrobić na dwa sposoby: | * Pokrywając większy prostokąt <math>2 \times n</math> musimy jakoś pokryć dwa skrajne pola przylegające do krótszej krawędzi o długości <math>2</math>. Można to zrobić na dwa sposoby: | ||
** ułożyć jedno domino pionowo - pozostanie prostokąt <math>2 \times (n - 1)</math>, który można pokryć na <math>d_{n-1}</math> sposobów, | ** ułożyć jedno domino pionowo - pozostanie prostokąt <math>2 \times (n - 1)</math>, który można pokryć na <math>d_{n-1}</math> sposobów, | ||
| Linia 410: | Linia 410: | ||
Czyli łącznie jest <math>d_n = d_{n-1}+d_{n-2}</math> sposobów pokrycia tablicy <math>2 \times n</math>. | Czyli łącznie jest <math>d_n = d_{n-1}+d_{n-2}</math> sposobów pokrycia tablicy <math>2 \times n</math>. | ||
Rozpoznajemy w tym łatwo ciąg Fibonacci'ego <math>d_n = f_{n+1}</math> (bo oczywiście pusty prostokąt <math>2 \times 0</math> można pokryć na dokładnie jeden sposób, <math>d_0= | Rozpoznajemy w tym łatwo ciąg Fibonacci'ego <math>d_n = f_{n+1}</math> (bo oczywiście pusty prostokąt <math>2 \times 0</math> można pokryć na dokładnie jeden sposób, <math>d_0=1</math>). | ||
}} | }} | ||
{{ | {{obserwacja|2.1|obs 2.1| | ||
<math>f_0+f_1+\ldots+f_n=f_{n+2}-1 | <math>f_0+f_1+\ldots+f_n=f_{n+2}-1</math>. | ||
}} | }} | ||
[[File:MD1-1.10.svg|350x150px|thumb|right|1.10]] | |||
{{dowod||| | {{dowod||| | ||
| Linia 428: | Linia 430: | ||
** jeśli na samym początku jest para poziomych domin, to pozostaje prostokąt <math>2\times (n-1)</math>, który możemy wypełnić dowolnie na <math>f_{n}</math> sposobów; | ** jeśli na samym początku jest para poziomych domin, to pozostaje prostokąt <math>2\times (n-1)</math>, który możemy wypełnić dowolnie na <math>f_{n}</math> sposobów; | ||
** jeśli na początku jest <math>i</math> (gdzie <math>0\leq i\leq n</math>) pionowych domin, a potem następuje para poziomych, to pozostaje prostokąt <math>2\times (n-i-1)</math>, który można wypełnić na <math>f_{n-i}</math> sposobów; | ** jeśli na początku jest <math>i</math> (gdzie <math>0\leq i\leq n</math>) pionowych domin, a potem następuje para poziomych, to pozostaje prostokąt <math>2\times (n-i-1)</math>, który można wypełnić na <math>f_{n-i}</math> sposobów; | ||
** para poziomych domin może się pojawić najdalej po <math>i=n-1</math> pionowych dominach | ** para poziomych domin może się pojawić najdalej po <math>i=n-1</math> pionowych dominach | ||
| Linia 436: | Linia 437: | ||
}} | }} | ||
{{ | [[File:MD1-1.11.mp4|250x250px|thumb|right|AM1.M15.W.R01]] | ||
{{obserwacja|2.2|obs 2.2| | |||
<math>f_0^2+f_1^2+\ldots+f_n^2=f_n\cdot f_{n+1}</math>.}} | |||
{{dowod||| | {{dowod||| | ||
| Linia 448: | Linia 450: | ||
* do założonej indukcyjnie równości <math>f_0^2+f_1^2+\ldots+f_k^2=f_k\cdot f_{k+1}</math> dodajmy obustronnie <math>f_{k+1}^2</math> otrzymując | * do założonej indukcyjnie równości <math>f_0^2+f_1^2+\ldots+f_k^2=f_k\cdot f_{k+1}</math> dodajmy obustronnie <math>f_{k+1}^2</math> otrzymując | ||
<center> | |||
<center><math>f_0^2+f_1^2+\ldots+f_k^2+f_{k+1}^2 = f_k\cdot f_{k+1}+f_{k+1}^2 = | <math>f_0^2+f_1^2+\ldots+f_k^2+f_{k+1}^2 = f_k\cdot f_{k+1}+f_{k+1}^2 = | ||
f_{k+1}\cdot(f_k+f_{k+1}) = f_{k+1}\cdot f_{k+2} | f_{k+1}\cdot(f_k+f_{k+1}) = f_{k+1}\cdot f_{k+2}</math>, | ||
</math></center> | </center> | ||
co kończy dowód kroku indukcyjnego. | co kończy dowód kroku indukcyjnego. | ||
| Linia 459: | Linia 460: | ||
{{twierdzenie|2.3 [wzór Eulera-Bineta]|tw 2.3| | {{twierdzenie|2.3 [wzór Eulera-Bineta]|tw 2.3| | ||
<center><math>f_n=\frac{1}{\sqrt{5}} | |||
\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right] | <center> | ||
</math></center> | <math>f_n=\frac{1}{\sqrt{5}} | ||
\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]</math> | |||
</center> | |||
| Linia 470: | Linia 473: | ||
<center><math>f^2-f-1=0 | <center> | ||
</math></center> | <math>f^2-f-1=0</math> | ||
</center> | |||
| Linia 493: | Linia 497: | ||
<center><math>x_1 = \frac{1+\sqrt{5}}{2} | <center><math>x_1 = \frac{1+\sqrt{5}}{2} | ||
\ \ \ \ \ \ \ \ \ \ | \ \ \ \ \ \ \ \ \ \ | ||
x_2 = \frac{1-\sqrt{5}}{2} | x_2 = \frac{1-\sqrt{5}}{2}</math></center> | ||
</math></center> | |||
| Linia 504: | Linia 507: | ||
Oznacza to w szczególności, że zbiór <math>F</math> ciągów spełniających zależność <math>f^{n+2}=f^{n+1}+f^n</math> jest podprzestrzenią wektorową przestrzeni <math>\mathbb{R}^\mathbb{N}</math>. | Oznacza to w szczególności, że zbiór <math>F</math> ciągów spełniających zależność <math>f^{n+2}=f^{n+1}+f^n</math> jest podprzestrzenią wektorową przestrzeni <math>\mathbb{R}^\mathbb{N}</math>. | ||
Przestrzen <math>F</math> jest dwuwymiarowa o bazie <math>\varphi, 1-\varphi</math> | '''Ćwiczenie''': ''Przestrzen <math>F</math> jest dwuwymiarowa o bazie <math>\varphi, 1-\varphi</math>'' | ||
Przypuśćmy na chwilę, że jakaś kombinacja liniowa ciągów <math>x_1^n, x_2^n</math>, tzn. | Przypuśćmy na chwilę, że jakaś kombinacja liniowa ciągów <math>x_1^n, x_2^n</math>, tzn. | ||
| Linia 524: | Linia 527: | ||
<center><math>\ | <center><math>\begin{align} c_1 &= \frac{f_1 - f_0x_2}{x_1-x_2}= \frac{1}{\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}} =\frac{1}{\sqrt{5}} | ||
\\ | \\ | ||
c_2 &= | c_2 &= \frac{f_1 - f_0x_1}{x_2-x_1}= \frac{1}{\frac{1-\sqrt{5}}{2}-\frac{1+\sqrt{5}}{2}} =-\frac{1}{\sqrt{5}} | ||
\ | \end{align}</math></center> | ||
| Linia 533: | Linia 536: | ||
<center><math>F(n) = \frac{1}{\sqrt{5}}\cdot\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n} - \left(\frac{1-\sqrt{5}}{2}\right)^{n}\right] | <center><math>F(n) = \frac{1}{\sqrt{5}}\cdot\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n} - \left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]</math>,</center> | ||
</math></center> | |||
jako potencjalnego kandydata na ciąg Fibonacci'ego. W istocie potrzebujemy indukcyjnego dowodu, że <math>F(n)=f_n</math>. Dla wygody oznaczmy <math>\varphi=\frac{1+\sqrt{5}}{2}</math>. | jako potencjalnego kandydata na ciąg Fibonacci'ego. W istocie potrzebujemy indukcyjnego dowodu, że <math>F(n)=f_n</math>. Dla wygody oznaczmy <math>\varphi=\frac{1+\sqrt{5}}{2}</math>. | ||
* Ponieważ liczby Fibonacci'ego są zadane wzorem odwołującym się | *Ponieważ liczby Fibonacci'ego są zadane wzorem odwołującym się do dwóch poprzednich elementów sprawdzamy dwie pierwsze wartości: | ||
do dwóch poprzednich elementów sprawdzamy dwie pierwsze wartości: | **<math>F(0)=\frac{1}{\sqrt{5}}\varphi^0-\frac{1}{\sqrt{5}}(1-\varphi)^0=\frac{1}{\sqrt{5}}-\frac{1}{\sqrt{5}}=0=f_0</math>, | ||
** <math>F(0)=\frac{1}{\sqrt{5}}\varphi^0-\frac{1}{\sqrt{5}}(1-\varphi)^0=\frac{1}{\sqrt{5}}-\frac{1}{\sqrt{5}}=0=f_0</math>, | |||
** <math>F(1)=\frac{1}{\sqrt{5}}\varphi-\frac{1}{\sqrt{5}}(1-\varphi)=\frac{1}{\sqrt{5}}(2\cdot\frac{1+\sqrt{5}}{2}-1)=1=f_1</math>, | ** <math>F(1)=\frac{1}{\sqrt{5}}\varphi-\frac{1}{\sqrt{5}}(1-\varphi)=\frac{1}{\sqrt{5}}(2\cdot\frac{1+\sqrt{5}}{2}-1)=1=f_1</math>, | ||
| Linia 547: | Linia 548: | ||
<center><math>\ | <center><math>\begin{align} F(k+2)&=\frac{1}{\sqrt{5}}\varphi^{k+2}-\frac{1}{\sqrt{5}}(1-\varphi)^{k+2}\\ | ||
&= | &=\frac{1}{\sqrt{5}}(\varphi^{k}+\varphi^{k+1})-\frac{1}{\sqrt{5}}((1-\varphi)^{k}+(1-\varphi)^{k+1})\\ | ||
&= | &=\frac{1}{\sqrt{5}}(\varphi^{k}-(1-\varphi)^{k})+\frac{1}{\sqrt{5}}(\varphi^{k+1}-(1-\varphi)^{k+1})\\ | ||
&= | &=F(k)+F(k+1)\\ | ||
&= | &=f_k+f_{k+1}\\ | ||
&= | &=f_{k+2}. | ||
\ | \end{align}</math></center> | ||
}} | }} | ||
[[grafika:Kepler.jpg|thumb|right||Jan Kepler (1571-1630)<br>[[Biografia Kepler|Zobacz biografię]]]] | |||
Liczba <math>\varphi=\frac{1+\sqrt{5}}{2}</math> jest powszechnie znana jako | Liczba <math>\varphi=\frac{1+\sqrt{5}}{2}</math> jest powszechnie znana jako | ||
'''złota liczba'''. Opisuje ona tak zwane złote proporcje w sztuce. Pojawia się ona również bardzo często przy okazji różnych obiektów kombinatorycznych. Występuje również w kolejnym wniosku, który po raz pierwszy zaobserwował Johannes Kepler. | {{kotwica|zlota|'''złota liczba'''}}. Opisuje ona tak zwane złote proporcje w sztuce. Pojawia się ona również bardzo często przy okazji różnych obiektów kombinatorycznych. Występuje również w kolejnym wniosku, który po raz pierwszy zaobserwował Johannes Kepler. | ||
| Linia 567: | Linia 567: | ||
<center><math>\lim_{n\rightarrow\infty}\frac{f_{n+1}}{f_n}=\varphi | <center> | ||
</math></center> | <math>\lim_{n\rightarrow\infty}\frac{f_{n+1}}{f_n}=\varphi</math> | ||
</center> | |||
| Linia 576: | Linia 577: | ||
<center><math>\ | <center> | ||
&= | <math>\begin{align} \lim_{n\rightarrow\infty}\frac{f_{n+1}}{f_n}&=\lim_{n\rightarrow\infty}\frac{\frac{1}{\sqrt{5}}(\varphi^{n+1}-(1-\varphi)^{n+1})}{\frac{1}{\sqrt{5}}(\varphi^n-(1-\varphi)^n)}\\ | ||
&= | &=\lim_{n\rightarrow\infty}\frac{\frac{1}{\sqrt{5}}\varphi-\frac{1}{\sqrt{5}}(1-\varphi)(\frac{1-\varphi}{\varphi})^n}{\frac{1}{\sqrt{5}}-\frac{1}{\sqrt{5}}(\frac{1-\varphi}{\varphi})^n}\\ | ||
\ | &=\varphi, | ||
\end{align}</math> | |||
</center> | |||
| Linia 585: | Linia 588: | ||
<center><math>\lim_{n\rightarrow\infty}\left(\frac{1-\varphi}{\varphi}\right)^n=0, | <center> | ||
</math></center> | <math>\lim_{n\rightarrow\infty}\left(\frac{1-\varphi}{\varphi}\right)^n=0, | ||
</math> | |||
</center> | |||
| Linia 597: | Linia 602: | ||
<center><math>\left[ | <center> | ||
<math>\left[ | |||
\begin{array} {cc} | \begin{array} {cc} | ||
f_{n+2}& f_{n+1} | f_{n+2}& f_{n+1} | ||
| Linia 603: | Linia 609: | ||
\end{array} | \end{array} | ||
\right] | \right] | ||
</math></center> | </math> | ||
</center> | |||
| Linia 609: | Linia 616: | ||
<center><math>\left[ | <center> | ||
<math>\left[ | |||
\begin{array} {cc} | \begin{array} {cc} | ||
f_{n+2}& f_{n+1} | f_{n+2}& f_{n+1} | ||
| Linia 631: | Linia 639: | ||
\end{array} | \end{array} | ||
\right]. | \right]. | ||
</math></center> | </math> | ||
</center> | |||
| Linia 637: | Linia 646: | ||
<center><math>\left[ | <center> | ||
<math>\left[ | |||
\begin{array} {cc} | \begin{array} {cc} | ||
f_2&f_1 | f_2&f_1 | ||
| Linia 651: | Linia 661: | ||
1&0 | 1&0 | ||
\end{array} | \end{array} | ||
\right] | \right]</math>, | ||
</math></center> | </center> | ||
| Linia 672: | Linia 682: | ||
1&0 | 1&0 | ||
\end{array} | \end{array} | ||
\right]^n | \right]^n</math></center> | ||
</math></center> | |||
Przyrównując wyznaczniki obu macierzy otrzymujemy tożsamość, którą jako pierwszy opublikował Jean-Dominique Cassini w 1680 roku. | [[grafika:Cassini.jpg|thumb|right||Giovanni Domenico Cassini (1625-1712)<br>[[Biografia Cassini|Zobacz biografię]]]]Przyrównując wyznaczniki obu macierzy otrzymujemy tożsamość, którą jako pierwszy opublikował Jean-Dominique Cassini w 1680 roku. | ||
{{ | {{obserwacja|2.5|obs 2.5| | ||
<math>f_{n+1}f_{n-1}-f_n^2=(-1)^n | <math>f_{n+1}f_{n-1}-f_n^2=(-1)^n</math>.}} | ||
Korzystając z kolei z faktu, że <math>A^mA^n=A^{m+n}</math> | Korzystając z kolei z faktu, że <math>A^mA^n=A^{m+n}</math> | ||
dla dowolnej kwadratowej macierzy <math>A</math>, otrzymujemy: | dla dowolnej kwadratowej macierzy <math>A</math>, otrzymujemy: | ||
{{ | {{obserwacja|2.6|obs 2.6| | ||
<center><math>\ | <center><math>\begin{align} f_n^2+f_{n-1}^2&=f_{2n-1},\\ | ||
f_{n+1}f_m+f_nf_{m-1}&= | f_{n+1}f_m+f_nf_{m-1}&=f_{m+n}. | ||
\ | \end{align}</math></center> | ||
| Linia 702: | Linia 710: | ||
<center><math>s_n = a\cdot s_{n-1} + b\cdot s_{n-2} | <center><math>s_n = a\cdot s_{n-1} + b\cdot s_{n-2}</math>,</center> | ||
</math></center> | |||
| Linia 743: | Linia 750: | ||
<center><math>c_1 = s_0 | <center><math>c_1 = s_0 | ||
\ \ \ \ \ \ \ \ | \ \ \ \ \ \ \ \ | ||
c_2 = \frac{s_1 - s_0x_0}{x_0} | c_2 = \frac{s_1 - s_0x_0}{x_0}</math></center> | ||
</math></center> | |||
==Drzewa binarne== | ==Drzewa binarne== | ||
| Linia 750: | Linia 756: | ||
Poznaliśmy wiele przykładów ciągów liczbowych zadanych równaniami rekurencyjnymi. Teraz poznamy zupełnie inną strukturę zadaną definicją rekurencyjną. | Poznaliśmy wiele przykładów ciągów liczbowych zadanych równaniami rekurencyjnymi. Teraz poznamy zupełnie inną strukturę zadaną definicją rekurencyjną. | ||
'''Drzewo binarne''' to dowolny obiekt powstały zgodnie z regułami: | [[File:MD1-1.12.svg|350x200px|thumb|right|Interpretacja graficzna kilku, małych drzew binarnych]] | ||
{{kotwica|dbin|'''Drzewo binarne'''}} to dowolny obiekt powstały zgodnie z regułami: | |||
* <math>\perp</math> jest drzewem binarnym, | * <math>\perp</math> jest drzewem binarnym, | ||
* jeśli <math>T_0</math> i <math>T_1</math> są drzewami binarnymi to <math>T_0\wedge T_1 </math> też jest drzewem binarnym. | * jeśli <math>T_0</math> i <math>T_1</math> są drzewami binarnymi to <math>T_0\wedge T_1</math> też jest drzewem binarnym. | ||
'''Zbiór wszystkich drzew binarnych''' oznaczamy przez <math>\mathbb{T}</math>. | {{kotwica|zdbin|'''Zbiór wszystkich drzew binarnych'''}} oznaczamy przez <math>\mathbb{T}</math>. | ||
Wypisując konkretne drzewo binarne używamy nawiasów aby ujednoznacznic kolejność aplikacji reguł z definicji rekurencyjnej. | Wypisując konkretne drzewo binarne używamy nawiasów aby ujednoznacznic kolejność aplikacji reguł z definicji rekurencyjnej. | ||
{{ | {{kotwica|wieldbin|'''Wielkość drzewa binarnego'''}} jest wyznaczona funkcją | ||
'''Wielkość drzewa binarnego''' jest wyznaczona funkcją | |||
<center><math>\mathbb{T} \ni T \mapsto \left\vert T\right\vert \in \mathbb{N} | <center> | ||
</math></center> | <math>\mathbb{T} \ni T \mapsto \left\vert T\right\vert \in \mathbb{N} | ||
</math> | |||
</center> | |||
| Linia 779: | Linia 782: | ||
* <math>\left\vert T_0\wedge T_1\right\vert=\left\vert T_0\right\vert+\left\vert T_1\right\vert+1</math>. | * <math>\left\vert T_0\wedge T_1\right\vert=\left\vert T_0\right\vert+\left\vert T_1\right\vert+1</math>. | ||
'''Szerokość drzewa binarnego''' jest wyznaczona funkcją | {{kotwica|sdbin|'''Szerokość drzewa binarnego'''}} jest wyznaczona funkcją | ||
<center><math>\mathbb{T} \ni T \mapsto \ | <center> | ||
</math></center> | <math>\mathbb{T} \ni T \mapsto \mathsf{ h}(T) \in \mathbb{N} | ||
</math> | |||
</center> | |||
zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako: | zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako: | ||
* <math>\ | * <math>\mathsf{ w}(\perp)=1</math>, | ||
* <math>\ | * <math>\mathsf{ w}(T_0\wedge T_1)=\mathsf{ w}(T_0)+\mathsf{ w}(T_1)</math>. | ||
'''Wysokość drzewa binarnego''' jest wyznaczona funkcją | {{kotwica|wysdbin|'''Wysokość drzewa binarnego'''}} jest wyznaczona funkcją | ||
<center><math>\mathbb{T} \ni T \mapsto \ | <center><math>\mathbb{T} \ni T \mapsto \mathsf{ h}(T) \in \mathbb{N} | ||
</math></center> | </math></center> | ||
| Linia 801: | Linia 806: | ||
zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako: | zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako: | ||
* <math>\ | * <math>\mathsf{ h}(\perp)=0</math>, | ||
* <math>\mathsf{ h}(T_0\wedge T_1)=\max\left(\mathsf{ h}(T_0),\mathsf{ h}(T_1) \right)+1</math>. | |||
[[File:MD1-1.13.svg|200x200px|thumb|right|1-13]] | |||
{{przyklad||| | {{przyklad||| | ||
<center> | |||
<math>\begin{align}\left\vert(\perp\wedge(\perp\wedge\perp))\wedge(\perp\wedge\perp)\right\vert&=\left\vert\perp\wedge(\perp\wedge\perp)\right\vert+\left\vert\perp\wedge\perp\right\vert+1\\ | |||
&=(\left\vert\perp\right\vert+\left\vert\perp\wedge\perp\right\vert+1)+(\left\vert\perp\right\vert+\left\vert\perp\right\vert+1)+1\\ | |||
<center><math>\ | &=(2+(\left\vert\perp\right\vert+\left\vert\perp\right\vert+1))+3+1\\ | ||
&= | &=9. | ||
&= | \end{align}</math> | ||
&= | </center> | ||
\ | |||
<center><math>\ | <center> | ||
&= | <math>\begin{align}\mathsf{ w}((\perp\wedge(\perp\wedge\perp))\wedge(\perp\wedge\perp)) | ||
&= | &=\mathsf{ w}(\perp\wedge(\perp\wedge\perp))+\mathsf{ w}(\perp\wedge\perp)\\ | ||
&= | &=(\mathsf{ w}(\perp)+\mathsf{ w}(\perp\wedge\perp))+(\mathsf{ w}(\perp)+\mathsf{ w}(\perp))\\ | ||
&= | &=(\mathsf{ w}(\perp)+(\mathsf{ w}(\perp)+\mathsf{ w}(\perp))+(\mathsf{ w}(\perp)+\mathsf{ w}(\perp))\\ | ||
\ | &=5. | ||
\end{align}</math> | |||
</center> | |||
<center><math>\ | <center> | ||
&= | <math>\begin{align}\mathsf{ h}((\perp\wedge(\perp\wedge\perp))\wedge(\perp\wedge\perp)) | ||
&= | &=\max\left(\mathsf{ h}(\perp\wedge(\perp\wedge\perp)),\mathsf{ h}(\perp\wedge\perp) \right)+1\\ | ||
&= | &=\max\left(\max\left(\mathsf{ h}(\perp),\mathsf{ h}(\perp\wedge\perp) \right)+1,\max\left(\mathsf{ h}(\perp),\mathsf{ h}(\perp) \right)+1 \right)+1\\ | ||
\ | &=4. | ||
\end{align}</math> | |||
</center> | |||
}} | }} | ||
[[File:MD1-1.14.svg|350x250px|thumb|right|1-14]] | |||
[[ | |||
{{ | {{obserwacja|2.7|obs 2.7| | ||
Dla <math>T=T_0\wedge T_1</math> mamy | Dla <math>T=T_0\wedge T_1</math> mamy | ||
* <math>\ | * <math>\mathsf{ h}(T_i)<\mathsf{ h}(T)</math>, | ||
* <math>\ | * <math>\mathsf{ w}(T_i)<\mathsf{ w}(T)</math>, | ||
* <math>\left\vert T_i\right\vert < \left\vert T\right\vert</math>.}} | * <math>\left\vert T_i\right\vert < \left\vert T\right\vert</math>.}} | ||
| Linia 864: | Linia 870: | ||
{{dowod||| | {{dowod||| | ||
Dla dowodu niewprost załóżmy, że w <math>S</math> nie ma wszystkich drzew. | Dla dowodu niewprost załóżmy, że w <math>S</math> nie ma wszystkich drzew. | ||
Zatem zbiór <math>S'=\mathbb{T}-S</math> jest niepusty. Tym samym niepusty jest też zbiór <math>Z={\left\{ {\ | Zatem zbiór <math>S'=\mathbb{T}-S</math> jest niepusty. Tym samym niepusty jest też zbiór <math>Z={\left\{ {\mathsf{ h}(T) : T \in S'} \right\}\ }</math> | ||
Na mocy założenia o <math>S</math> wiemy, że <math>\perp\notin S'</math>, | Na mocy założenia o <math>S</math> wiemy, że <math>\perp\notin S'</math>, | ||
co wraz z [[#wn_2.8|Wnioskiem 2.8]] implikuje, że <math>0\notin Z</math>. | co wraz z [[#wn_2.8|Wnioskiem 2.8]] implikuje, że <math>0\notin Z</math>. | ||
Ponieważ <math>Z</math> jest niepusty, to na podstawie Zasady Minimum | Ponieważ <math>Z</math> jest niepusty, to na podstawie Zasady Minimum | ||
ma element najmniejszy, powiedzmy <math>z</math>. Wiemy już, że <math>z>0</math>. Niech <math>T\in S'</math> poświadcza fakt, że <math>z\in Z</math>, tzn. <math>\ | ma element najmniejszy, powiedzmy <math>z</math>. Wiemy już, że <math>z>0</math>. Niech <math>T\in S'</math> poświadcza fakt, że <math>z\in Z</math>, tzn. <math>\mathsf{ h}(T)=z>0</math>. Ponownie z [[#wn_2.8|Wniosku 2.8]] dostajemy <math>T'\neq\perp</math>, czyli <math>T'=T_0\wedge T_1</math> dla pewnych <math>T_1,T_2</math>. Z [[#obs_2.7|Obserwacji 2.7]] mamy <math>\mathsf{ h}(T_0)<\mathsf{ h}(T)=z</math> oraz <math>\mathsf{ h}(T_1)<\mathsf{ h}(T)=z</math>. Zatem minimalność <math>z</math> w <math>S_0'</math> daje <math>\mathsf{ h}(T_0),\mathsf{ h}(T_1)\notin Z</math>, czyli <math>T_0,T_1\notin S'</math> i w konsekwencji <math>T_0,T_1\in S</math>. | ||
Ale wtedy, z założenia o zbiorze <math>S</math>, dostajemy <math>T=T_0\wedge T_1=T\in S</math>. Sprzeczność. | Ale wtedy, z założenia o zbiorze <math>S</math>, dostajemy <math>T=T_0\wedge T_1=T\in S</math>. Sprzeczność. | ||
| Linia 876: | Linia 882: | ||
Zasada Indukcji dla drzew binarnych to przykład na to, że w strukturach zdefiniowanych rekurencyjnie można dowodzić przy pomocy zasady analogicznej do Zasady Indukcji. Poniżej przedstawiamy przykład używający tego narzędzia. | Zasada Indukcji dla drzew binarnych to przykład na to, że w strukturach zdefiniowanych rekurencyjnie można dowodzić przy pomocy zasady analogicznej do Zasady Indukcji. Poniżej przedstawiamy przykład używający tego narzędzia. | ||
{{ | {{obserwacja|2.10|obs 2.10| | ||
Dla dowolnego drzewa binarnego <math>T\in\mathbb{T}</math> mamy: | Dla dowolnego drzewa binarnego <math>T\in\mathbb{T}</math> mamy: | ||
* <math>\ | * <math>\mathsf{ h}(T) \le \mathsf{ w}(T) \le \left\vert T\right\vert</math>, | ||
* <math>\left\vert T\right\vert=2\cdot\ | * <math>\left\vert T\right\vert=2\cdot\mathsf{ w}(T)-1</math>.}} | ||
{{dowod||| | {{dowod||| | ||
Niech <math>S\subseteq\mathbb{T}</math> będzie zbiorem drzew binarnych spełniających powyższe własności. | Niech <math>S\subseteq\mathbb{T}</math> będzie zbiorem drzew binarnych spełniających powyższe własności. | ||
* <math>\ | * <math>\mathsf{ h}(\perp)=0 \le 1 =\mathsf{ w}(\perp)= \left\vert\perp\right\vert</math>, oraz <math>\left\vert\perp\right\vert=1=2\mathsf{ w}(\perp)-1</math>, czyli <math>\perp\in S</math>. | ||
* W kroku indukcyjnym zakładamy, że <math>T=T_0\wedge T_1</math> oraz że drzewa <math>T_0,T_1</math> mają już opisane w Obserwacji własności. Wtedy | * W kroku indukcyjnym zakładamy, że <math>T=T_0\wedge T_1</math> oraz że drzewa <math>T_0,T_1</math> mają już opisane w Obserwacji własności. Wtedy | ||
<center><math>\ | <center><math>\begin{align}\left\vert T_0\wedge T_1\right\vert&=\left\vert T_0\right\vert+\left\vert T_1\right\vert+1 | ||
=(2\ | =(2\mathsf{ w}(T_0)-1)+(2\mathsf{ w}(T_1)-1)+1\\ | ||
&= | &=2(\mathsf{ w}(T_0)+\mathsf{ w}(T_1))-1\\ | ||
&= | &=2\mathsf{ w}(T_0\wedge T_1)-1. | ||
\ | \end{align}</math></center> | ||
| Linia 901: | Linia 907: | ||
<center><math>\ | <center><math>\begin{align}\mathsf{ h}(T_0\wedge T_1) | ||
&= | &=\max\left(\mathsf{ h}(T_0),\mathsf{ h}(T_1) \right)+1 | ||
\\ | \\ | ||
&\leq | &\leq \max\left(\mathsf{ w}(T_0),\mathsf{ w}(T_1) \right)+1 | ||
\\ | \\ | ||
&\leq | &\leq \mathsf{ w}(T_0)+\mathsf{ w}(T_1) | ||
\\ | \\ | ||
&= | &=\mathsf{ w}(T_0\wedge T_1), | ||
\ | \end{align}</math></center> | ||
gdzie ostatnia nierówność wynika bezpośrednio z faktu, że szerokość każdego drzewa wynosi co najmniej <math>1</math>. | gdzie ostatnia nierówność wynika bezpośrednio z faktu, że szerokość każdego drzewa wynosi co najmniej <math>1</math>. | ||
}} | }} | ||
Aktualna wersja na dzień 21:48, 11 wrz 2023
Definicje rekurencyjne
Definicja rekurencyjna (indukcyjna):
- nieformalnie - taka definicja, która odwołuje się do samej siebie - ale trzeba tu uważać, by odwołanie było do instancji o mniejszej komplikacji,
- zwykle chodzi o ciąg , - dla którego przepis na element wykorzystuje jakieś poprzednie elementy: itp.,
- początkowy element (lub kilka początkowych) muszą być zadane konkretnie - żeby było od czego zacząć,
- zwykle definicja rekurencyjna odwołuje się do jednego lub kilku poprzednich elementów, ale może też odwoływać się do wszystkich poprzednich.
Przykład
Silnia liczby (zapisywana jako ) to iloczyn kolejnych liczb naturalnych od do , czyli
Przyjmuje się że . Oto wartości silni dla kilku początkowych liczb naturalnych
Ciąg aby mógł być precyzyjnie rozumiany np. przez komputer, powinien być zadany rekurencyjnie jako:
Ponieważ pierwszy wyraz jest zadany, to możemy kolejno obliczać:
Przykład
Jaki ciąg jest zdefiniowany poprzez małą modyfikację w definicji silni?
A co definiują następujące określenia:
oraz
W ostatnim przypadku widać, że ponieważ odwołanie jest dwa wyrazy wstecz, to już wyliczenie pierwszego wyrazu staje się niemożliwe.
Ciąg arytmetyczny
Przykład
W ciągu zadanym poprzez równania:
łatwo rozpoznać kolejne liczby parzyste:
Ogólnie ciąg zadany poprzez ustalenie oraz
to tzw. ciąg arytmetyczny.
Jego -ty wyraz dany jest wzorem:
Aby to uzasadnić, pokazujemy indukcyjnie, że:
oraz
Ciąg geometryczny
Przykład
W ciągu zadanym poprzez równania:
łatwo rozpoznać kolejne potęgi liczby :
Ogólnie ciąg zadany poprzez ustalenie oraz zadanie
to tzw. ciąg geometryczny.
Jego -ty wyraz dany jest wzorem:
Aby to uzasadnić, pokazujemy indukcyjnie, że:
oraz
Wieże Hanoi
Przykład (E.Lucas, 1883)
U zarania czasu Bóg umieścił 64 złote krążki na jednej z trzech diamentowych iglic tak, że krążki wyżej umieszczone miały mniejsze promienie.
Następnie Bóg polecił grupie mnichów przełożenie tych krążków na trzecią iglicę , ale tak by:
- w jednym ruchu przenosić tylko jeden krążek,
- krążek większy nigdy nie może leżeć na krążku mniejszym,
- można posługiwać się iglicą .
Mnisi pracują od zarania dziejów dzień i noc ... .Ile czasu im to zajmie?
Wieże Hanoi - analiza
By obliczyć ilość potrzebnych do wykonania ruchów, przeanalizujmy najpierw małe przypadki:
Łatwo zauważyć, że dla 1 krążka potrzebny jest jeden ruch:
Podobnie dla dwu krążków możemy postąpić:
Przy 3 krążkach postępujemy tak:
- najpierw przenosimy dwa górne krążki na iglicę posługując się iglicą :
- przenosimy największy krążek z na :
- przenosimy krążki z na posługując się iglicą :
co pokazuje, że potrzeba tu 7 ruchów.
Czy już wiesz jak rozwiązać to zadanie w ogólności (dla krążków)?
Oznaczmy przez liczbę ruchów potrzebnych do przeniesienia krążków z jednej iglicy na drugą. Wiemy już, że:
Aby przenieść krążków z na możemy postąpić podobnie jak w przypadku 3 krążków, redukując zadanie do:
- przenosimy górnych krążków na iglicę posługując się iglicą - potrzeba na to ruchów
- przenosimy największy krążek z na - to tylko jeden ruch
- przenosimy krążków z na posługując się iglicą - znów potrzeba na to ruchów
A zatem
Ile wobec tego wynosi ?
Mamy więc równanie rekurencyjne
bardzo podobne do ciągu geometrycznego.
Możemy policzyć kilka jego wyrazów:
i rozpoznać w nim ciąg potęg dwójki zmniejszonych o 1.
Ale czy rzeczywiście ?
I znów, aby się upewnić, że nasze odgadnięcie było poprawne, sprawdzamy indukcyjnie, że
co oznacza, że rzeczywiście ciąg spełnia równanie rekurencyjne, którym zadany jest ciąg .
A wiec ,
co przy przenoszeniu jednego krążka na sekundę zajmie ponad lat, a przenosząc te krążki "komputerem" 3GHz potrzeba będzie... i tak ponad tysiąc lat!
Przykład
Przykład
Jaka jest największa możliwa liczba obszarów wyznaczonych przez prostych na płaszczyźnie?
Sprawdźmy najpierw kilka pierwszych wartości.
- Gdy nie ma żadnej prostej obszar jest jeden.
- Jedna prosta tworzy zawsze dwa różne obszary.
- Kładąc drugą prostą (byle nie równoległą do pierwszej) otrzymujemy obszary.
W tym momencie możemy pokusić się o zgadywanie i przypuścić, że . Jednakże
- Dla trzech prostych jest to .
Zauważmy, że nowa prosta zwiększa ilość obszarów o jeśli przecina dokładnie z poprzednich prostych i to w nowych punktach przecięć. Z drugiej strony dwie proste mogą się przeciąć w co najwyżej jednym punkcie i przecinają się o ile nie są równolegle. Widzimy zatem, że najwięcej obszarów dostaniemy kładąc kolejne proste w ten sposób aby żadne dwie nie były równoległe i żadne trzy nie przecinały się w jednym punkcie. Otrzymujemy następujące równanie rekurencyjne:
Ponownie rozwiążemy równanie rozwijając je:
gdzie ostatnia równość wynika z - już udowodnionego - wzoru na sumę kolejnych liczb naturalnych.
Liczby Fibonacciego

Zobacz biografię
Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego zadany przez
Wszystkie wyrazy ciągu, oprócz pierwszych dwu, są sumą dwu poprzednich elementów. Oto kilka pierwszych wartości ciągu Fibonacciego:
- Jak odgadnąć wzór na ogólny wyraz ciągu?
- Jeśli nie można odgadnąć, to jak oszacować szybkość wzrostu tego ciągu?
- Czy rośnie on wielomianowo czy raczej wykładniczo?
Pierwsze pytanie - póki co - wydaje się dość beznadziejne.
Przykład
Na ile sposobów można ułożyć domina na prostokącie o rozmiarze ?
Oznaczmy, tę liczbę przez w zależności od .
- Dla jest to możliwe na dokładnie jeden sposób, tzn.
- Dla są już dwa takie sposoby:
- ustawiamy obie kostki poziomo, lub obie pionowo,
a zatem .
- Dla są trzy sposoby,
- Pokrywając większy prostokąt musimy jakoś pokryć dwa skrajne pola przylegające do krótszej krawędzi o długości . Można to zrobić na dwa sposoby:
- ułożyć jedno domino pionowo - pozostanie prostokąt , który można pokryć na sposobów,
- ułożyć dwa domina poziomo - pozostanie prostokąt , który można pokryć na sposobów.
Czyli łącznie jest sposobów pokrycia tablicy .
Rozpoznajemy w tym łatwo ciąg Fibonacci'ego (bo oczywiście pusty prostokąt można pokryć na dokładnie jeden sposób, ).
Obserwacja 2.1
.
Dowód
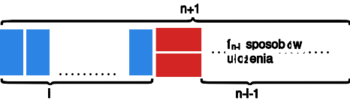
Polecamy jako ćwiczenie bardzo łatwy dowód powyższej równości przez indukcję. Przedstawimy alternatywny dowód posługujący się intuicją z poprzedniego przykładu. Wiemy zatem, że prostokąt wielkości można pokryć kostkami domina na sposobów.
Dla dowodu obserwacji, policzmy na ile sposobów można ułożyć prostokąt wielkości w taki sposób aby było tam chociaż jedno domino ustawione poziomo. Policzymy to dwiema różnymi metodami:
- Jest tylko jedna metoda ułożenia prostokąta bez poziomych klocków. A zatem jest sposobów ułożenia prostokąta z chociaż jednym dominem poziomym.
- Rozważmy kolejne możliwe miejsca pierwszego poziomego domina (tak naprawdę pary domin) w prostokącie od lewej:
- jeśli na samym początku jest para poziomych domin, to pozostaje prostokąt , który możemy wypełnić dowolnie na sposobów;
- jeśli na początku jest (gdzie ) pionowych domin, a potem następuje para poziomych, to pozostaje prostokąt , który można wypełnić na sposobów;
- para poziomych domin może się pojawić najdalej po pionowych dominach
To dowodzi, iż jest dokładnie sposobów ułożenia prostokąta z chociaż jednym dominem poziomym.
Policzyliśmy na dwa różne sposoby to samo, otrzymując obie strony postulowanej równości. To kończy dowód.
Obserwacja 2.2
Dowód
Dowód przez indukcję po :
- dla mamy ,
- do założonej indukcyjnie równości dodajmy obustronnie otrzymując
,
co kończy dowód kroku indukcyjnego.
Twierdzenie 2.3 [wzór Eulera-Bineta]
Dowód
Rozważmy równanie:
Mnożąc je obustronnie przez otrzymujemy:
Oznacza to, że jeśli jest pierwiastkiem równania , to ciąg spełnia zależność rekurencyjną Fibonacci'ego:
Tyle, że równanie ma dwa rzeczywiste rozwiązania:
Który więc z ciągów jest ciągiem Fibonacci'ego? Okazuje się, że żaden, bo na przykład ilorazy kolejnych wyrazów ciągu Fibonacci'ego nie są stałe, a takie musiałyby być dla ciągów geometrycznych . Co więcej:
- jeśli ciąg spełnia zależność , to dla dowolnej liczby rzeczywistej ciąg też spełnia tę zależność,
- jeśli ciągi i spełniają zależność , to ich suma też spełnia tę zależność.
Oznacza to w szczególności, że zbiór ciągów spełniających zależność jest podprzestrzenią wektorową przestrzeni .
Ćwiczenie: Przestrzen jest dwuwymiarowa o bazie
Przypuśćmy na chwilę, że jakaś kombinacja liniowa ciągów , tzn.
jest poszukiwanym ciągiem Fibonacci'ego. Aby wyznaczyć stałe zauważmy, że muszą one spełniać układ równań:
co po rozwiązaniu daje:
i ostatecznie dostajemy ciąg:
jako potencjalnego kandydata na ciąg Fibonacci'ego. W istocie potrzebujemy indukcyjnego dowodu, że . Dla wygody oznaczmy .
- Ponieważ liczby Fibonacci'ego są zadane wzorem odwołującym się do dwóch poprzednich elementów sprawdzamy dwie pierwsze wartości:
- ,
- ,
- Aby pokazać, że użyjemy pod koniec naszych obliczeń założenia indukcyjnego, że i , a także tego, że zarówno jak i spełniają zależność :

Zobacz biografię
Liczba jest powszechnie znana jako złota liczba. Opisuje ona tak zwane złote proporcje w sztuce. Pojawia się ona również bardzo często przy okazji różnych obiektów kombinatorycznych. Występuje również w kolejnym wniosku, który po raz pierwszy zaobserwował Johannes Kepler.
Wniosek 2.4
Dowód
Macierze liczb Fibonacci'ego
Rozważając specjalne kwadratowe macierze liczb Fibonacci'ego postaci
łatwo zauważamy, że
Ponieważ równocześnie:
,
to łatwo indukcyjnie łatwo udowodnić, że

Zobacz biografię
Przyrównując wyznaczniki obu macierzy otrzymujemy tożsamość, którą jako pierwszy opublikował Jean-Dominique Cassini w 1680 roku.
Obserwacja 2.5
Korzystając z kolei z faktu, że dla dowolnej kwadratowej macierzy , otrzymujemy:
Obserwacja 2.6
Rozwiązywanie liniowych równań rekurencyjnych - metoda ogólna
Rozumowanie dotyczące ciągu Fibonacci'ego możemy uogólnić. Chwilowo skupimy się jedynie na przypadku, gdy dla rozwiązania równania rekurencyjnego
równanie kwadratowe
ma dokładnie dwa różne pierwiastki . Wtedy bowiem łatwo pokazać, że ciąg
ze stałymi
jest poszukiwanym rozwiązaniem.
Gdy równanie ma tylko jeden pierwiastek (podwójny, gdy ), to wkrótce pokażemy, że rozwiązaniem jest
ze stałymi wyznaczonymi, jak poprzednio, poprzez dwa pierwsze wyrazy początkowe:
Drzewa binarne
Poznaliśmy wiele przykładów ciągów liczbowych zadanych równaniami rekurencyjnymi. Teraz poznamy zupełnie inną strukturę zadaną definicją rekurencyjną.
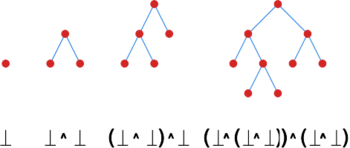
Drzewo binarne to dowolny obiekt powstały zgodnie z regułami:
- jest drzewem binarnym,
- jeśli i są drzewami binarnymi to też jest drzewem binarnym.
Zbiór wszystkich drzew binarnych oznaczamy przez . Wypisując konkretne drzewo binarne używamy nawiasów aby ujednoznacznic kolejność aplikacji reguł z definicji rekurencyjnej.
Wielkość drzewa binarnego jest wyznaczona funkcją
zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako:
- ,
- .
Szerokość drzewa binarnego jest wyznaczona funkcją
zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako:
- ,
- .
Wysokość drzewa binarnego jest wyznaczona funkcją
zdefiniowana rekurencyjnie (z uwagi na budowę drzewa) jako:
- ,
- .

Przykład
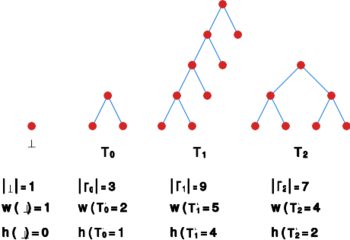
Obserwacja 2.7
Dla mamy
- ,
- ,
- .
Wniosek 2.8
Twierdzenie 2.9 [Zasada Indukcji dla drzew binarnych]
Gdy jest zbiorem drzew binarnych spełniającym warunki:
- ,
- jeśli to ,
to .
Dowód
Dla dowodu niewprost załóżmy, że w nie ma wszystkich drzew. Zatem zbiór jest niepusty. Tym samym niepusty jest też zbiór Na mocy założenia o wiemy, że , co wraz z Wnioskiem 2.8 implikuje, że .
Ponieważ jest niepusty, to na podstawie Zasady Minimum ma element najmniejszy, powiedzmy . Wiemy już, że . Niech poświadcza fakt, że , tzn. . Ponownie z Wniosku 2.8 dostajemy , czyli dla pewnych . Z Obserwacji 2.7 mamy oraz . Zatem minimalność w daje , czyli i w konsekwencji .
Ale wtedy, z założenia o zbiorze , dostajemy . Sprzeczność.
Zasada Indukcji dla drzew binarnych to przykład na to, że w strukturach zdefiniowanych rekurencyjnie można dowodzić przy pomocy zasady analogicznej do Zasady Indukcji. Poniżej przedstawiamy przykład używający tego narzędzia.
Obserwacja 2.10
Dla dowolnego drzewa binarnego mamy:
- ,
- .
Dowód