SW wykład 9 - Slajd1

<<powrót do strony wykładu

Dziedziny podstawowe Suma i produkt Suma spłaszczona i produkt spłaszczony Przestrzeń funkcji ciągłych Izomorfizm dziedzin Konstruowanie funkcji ciągłych Złożenie funkcji i indeksowanie Inne konstrukcje Operator punktu stałego Równania stałopunktowe Równania dziedzinowe Rekurencyjne równania dziedzinowe Rekurencyjne równania dziedzinowe Problemy Dziedziny refleksywne Rozwiązanie naiwne dziedziny Scotta

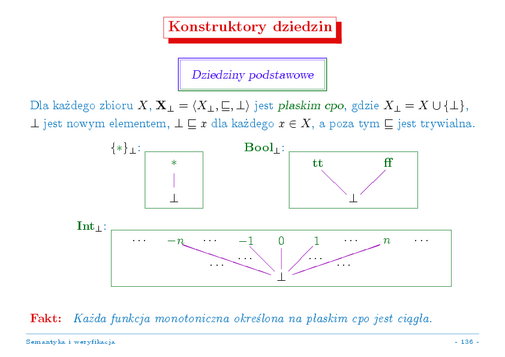
Zacznijmy od konstruowania najprostszych dziedzin semantycznych jako zbiorów łańcuchowo zupełnych.

Dla dowolnego zbioru danych tworzymy z niego zbiór łańcuchowo zupełny dodając nowy, "sztuczny" element najmniejszy. Owo dodane "denko" jest w relacji porządku ze wszystkimi elementami tego zbioru (i, oczywiscie, też ze sobą); każdy inny element jest w relacji tylko z samym sobą.

W tak utworzonym zbiorze łańcuchowo zupełnym jedyne więcej niż jednoelementowe łańcuchy składają się z denka i pewnego elementu z pierwotnego zbioru. Nieformalnie: w takich "płaskich" zbiorach łańcuchowo zupełnych mamy do czynienia jedynie z elementem "nieokreślonym" (najmniejszym w zbiorze) i z elementami "w pełni określonymi" (wszystkie pozostałe elementy są w tym porządku maksymalne).

Łatwo też sprawdzić, że ciągłość funkcji na takich zbiorach jest równoważna jej monotoniczności. Własność tę można uogólnić na wszystkie zbiory łańcuchowo zupełne, w których wszystkie łańcuchy są skończone.

Podobnie definiujemy operację "podnoszenia" dowolnego zbioru łańcuchowo zupełnego przez dodanie do niego nowego elementu najmniejszego (z zachowaniem porządku na dotychczasowych elementach). Łatwo widać, że operacja ta buduje zbiór łańcuchowo zupełny ze zbioru łańcuchowo zupełnego.