CWGI Ćwiczenie 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 4 wersji utworzonych przez 2 użytkowników) | |||
| Linia 9: | Linia 9: | ||
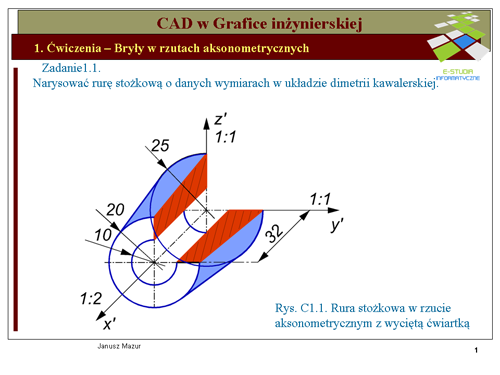
Układ dimetrii kawalerskiej pozwala przedstawiać elementy płaskie, bez zniekształceń, znajdujące się w płaszczyźnie <math>0yz\ | Układ dimetrii kawalerskiej pozwala przedstawiać elementy płaskie, bez zniekształceń, znajdujące się w płaszczyźnie <math>0yz\ </math>,. Przekrojem poprzecznym rury będą okręgi. Należy, zatem przyjąć takie usytuowanie rury w układzie dimetrii kawalerskiej, aby oś rury pokrywała się z kierunkiem osi x (przekrój poprzeczny rury będzie wówczas znajdował się na rzucie <math>0yz\ </math>,. Rozpoczynając rysowanie dokonujemy analizy skrótów aksonometrycznych w poszczególnych osiach. W kierunku osi <math>x\ </math>, skrót aksonometryczny wynosi 1:2, a więc wymiary rury w tym kierunku będą zmniejszone o połowę. Mając takie informacje można rozpocząć konstruowanie rury. Dla pokazania przelotowości rury i jej wnętrza wyznaczamy widok z wycięta ćwiartka na całej długości (rys.C1.1). | ||
|} | |} | ||
| Linia 21: | Linia 21: | ||
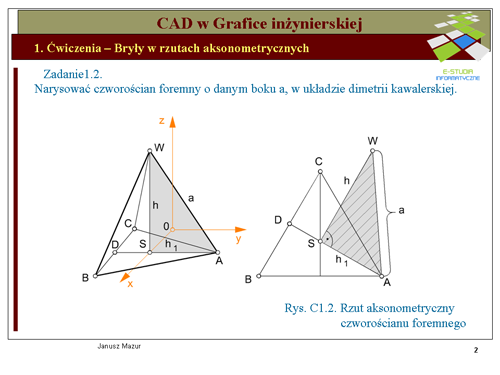
Czworościan foremny jest bryłą, której wszystkie ściany są trójkątami równobocznymi (przyjmujemy wielkość boku a = 50 mm). Na rysunku C1.2. przedstawiono, po prawej stronie, trójkąt ABC, który jest podstawą tego czworościanu. Wyznaczając wysokości trójkąta, można wyznaczyć spodek wysokości czworościanu, a następnie budując trójkąt prostokątny w oparciu o znaną przyprostokątną (2/3 wysokości trójkąta - <math>AS\ | Czworościan foremny jest bryłą, której wszystkie ściany są trójkątami równobocznymi (przyjmujemy wielkość boku a = 50 mm). Na rysunku C1.2. przedstawiono, po prawej stronie, trójkąt ABC, który jest podstawą tego czworościanu. Wyznaczając wysokości trójkąta, można wyznaczyć spodek wysokości czworościanu, a następnie budując trójkąt prostokątny w oparciu o znaną przyprostokątną (2/3 wysokości trójkąta - <math>AS\ </math>,) oraz przeciwprostokątną <math>AW\ </math>, - krawędź <math>a\ </math>, czworościanu) otrzymamy wszystkie jego wielkości geometryczne, niezbędne do budowy bryły w układzie aksonometrycznym, a w szczególności wysokość <math>h\ </math>, czworościanu będącą rzeczywista wielkością odcinka <math>SW\ </math>,. | ||
Rozwiązanie zadania rozpoczynamy od wykreślenia układu aksonometrycznego - perspektywy kawalerskiej. Przypominając, w osiach <math>y\ | Rozwiązanie zadania rozpoczynamy od wykreślenia układu aksonometrycznego - perspektywy kawalerskiej. Przypominając, w osiach <math>y\ </math>, i <math>z\ </math>,, skrót aksonometryczny wynosi 1:1, natomiast w osi <math>x\ </math>, wynosi 1:2. Podstawę czworościanu wykreślimy przyjmując w niezmienionej wielkości wysokość <math>AD\ </math>, podstawy i umieszczając ją równolegle do osi <math>y\ </math>,, przyjmując w pierwszej kolejności spodek wysokości <math>S\ </math>, w dowolnym punkcie na osi <math>y\ </math>,. Bok <math>BC\ </math>,, prostopadły do wysokości <math>AD\ </math>,, przyjmie kierunek osi <math>x\ </math>,. Wielkość boku <math>BC\ </math>, będzie oczywiście o połowę mniejsza od rzeczywistej, ponieważ skrót aksonometryczny w kierunku tej osi wynosi 1:2. Ze spodka wysokości w niezmienionej wielkości wykreślamy wysokość czworościanu, wyznaczając wierzchołek <math>W\ </math>, czworościanu. Łącząc wierzchołek <math>W\ </math>, czworościanu z wierzchołkami <math>A, B, C\ </math>, wyznaczymy zarys bryły. Na zakończenie należy uwzględnić widoczność krawędzi obserwując bryłę z kierunku prostopadłego do płaszczyzny określonej osiami <math>y, z\ </math>,. Krawędzie widoczne rysuje się linią grubą ciągłą, krawędzie niewidoczne linią | ||
|} | |} | ||
| Linia 33: | Linia 33: | ||
|valign="top"|''Zadanie1.3.'' | |valign="top"|''Zadanie1.3.'' | ||
''Narysować sześcian o danym boku w dowolnym rzucie aksonometrycznym. Wyznaczyć przekrój sześcianu płaszczyzna określona przez trzy punkty <math>(P,Q,R)\ | ''Narysować sześcian o danym boku w dowolnym rzucie aksonometrycznym. Wyznaczyć przekrój sześcianu płaszczyzna określona przez trzy punkty <math>(P,Q,R)\ </math>,, leżące na ścianach bocznych sześcianu'' | ||
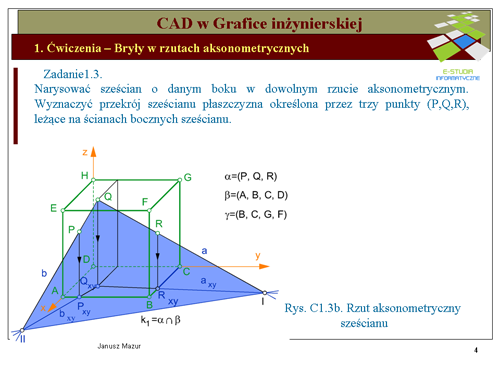
Korzystając z niezmienników rzutowania równoległego i twierdzenia o punkcie wspólnym trójki płaszczyzn, rysujemy rzut sześcianu o boku <math>a = 30 mm</math> w układzie perspektywy kawalerskiej. | Korzystając z niezmienników rzutowania równoległego i twierdzenia o punkcie wspólnym trójki płaszczyzn, rysujemy rzut sześcianu o boku <math>a = 30 mm</math> w układzie perspektywy kawalerskiej. | ||
Obieramy dowolną trójkę punktów <math>P, Q, R,\ | Obieramy dowolną trójkę punktów <math>P, Q, R,\ </math>, leżących na jego ścianach bocznych (rys.C1.3a). | ||
Zadanie rozwiążemy wykorzystując twierdzenie '''''"o punkcie wspólnym trójki płaszczyzn"'''''. W tym celu przyjmijmy symboliczny opis trzech wybranych płaszczyzn, z których jedna jest płaszczyzną <math>\alpha (PQR)\ | Zadanie rozwiążemy wykorzystując twierdzenie '''''"o punkcie wspólnym trójki płaszczyzn"'''''. W tym celu przyjmijmy symboliczny opis trzech wybranych płaszczyzn, z których jedna jest płaszczyzną <math>\alpha (PQR)\ </math>,, krojącą poszczególne ściany sześcianu. Dla ściślejszego zdefiniowania poszczególnych punktów <math>PQR\ </math>,, w założeniach podano rzuty prostopadłe tych punktów na płaszczyznę podstawy <math>ABCD\ </math>,, którą opiszemy symbolicznie literą <math>\beta\ </math>,. Jako trzecią z płaszczyzn, biorących udział w konstrukcji przyjmijmy ścianę <math>BCFG\ </math>, jako <math>\gamma\ </math>,. | ||
Zadaniem naszym jest wyznaczenie krawędzi przecięcia się płaszczyzny <math>\alpha (PQR)\ | Zadaniem naszym jest wyznaczenie krawędzi przecięcia się płaszczyzny <math>\alpha (PQR)\ </math>, ze ścianami sześcianu. | ||
|} | |} | ||
| Linia 51: | Linia 51: | ||
|valign="top"|Krawędzie poszczególnych par płaszczyzn oznaczymy kolejno: | |valign="top"|Krawędzie poszczególnych par płaszczyzn oznaczymy kolejno: | ||
<math>k_1=\alpha \cap \beta\ | <math>k_1=\alpha \cap \beta\ </math>, <math>k_2=\beta \cap \gamma\ </math>, <math>k_3=\alpha \cap \gamma\ </math> | ||
Wyznaczając konstrukcyjnie krawędzie <math>k_1\ | Wyznaczając konstrukcyjnie krawędzie <math>k_1\ </math> i <math>k_2\ </math>, możemy następnie, korzystając z twierdzenia o punkcie wspólnym trójki płaszczyzn, wyznaczyć poszukiwaną w zadaniu krawędź <math>k_3\ </math>. | ||
'''Wyznaczanie krawędzi <math>k_1\ | '''Wyznaczanie krawędzi <math>k_1\ </math>''' | ||
Poprowadźmy dwie proste należące do płaszczyzny <math>\alpha (PQR)\ | Poprowadźmy dwie proste należące do płaszczyzny <math>\alpha (PQR)\ </math>: prostą <math>a\ </math>, przechodzącą przez punkty <math>Q\ </math>,, <math>R\ </math>, oraz prostą b przechodzącą przez punkty <math>Q\ </math>,, <math>P\ </math>,. Proste te przecinają się w punkcie <math>Q\ </math>,. Rzuty <math>a_{xy}\ </math> i <math>b_{xy}\ </math> tych prostych na płaszczyznę podstawy <math>\beta (ABCD)\ </math>, będą przecinały się w punkcie <math>Q_{xy}\ </math>. Proste <math>a\ </math> i <math>a_{xy}\ </math> przecinają się w punkcie oznaczonym cyfrą <math>I\ </math>,. Punkt <math>I\ </math>, jest, zatem wspólnym dla płaszczyzn <math>\alpha\ </math> i <math>\beta\ </math>, ponieważ należy do prostych <math>a\ </math> i <math>a_{xy}\ </math>, a te z kolei należą odpowiednio do płaszczyzn <math>\alpha\ </math> i <math>\beta\ </math>. Drugi punkt <math>II\ </math>, wspólny płaszczyzn <math>\alpha\ </math> i <math>\beta\ </math> wyznaczymy prowadząc dwie, należące odpowiednio do płaszczyzn <math>\alpha \cap \beta\ </math>, kolejne proste <math>b\ </math> i <math>b_{xy}\ </math> które przetną się właśnie w tym punkcie. Łącząc punkty <math>I\ </math>, i <math>II\ </math>, wyznaczymy pierwsza z poszukiwanych krawędzi <math>k_1 =\alpha \cap \beta\ </math>. Jak widać na rysunku C1.3b krawędź <math>k_1\ </math> leży na płaszczyźnie <math>\beta (ABCD)\ </math>,, lecz nie przecina ściany <math>ABCD\ </math>, sześcianu. | ||
|} | |} | ||
| Linia 69: | Linia 69: | ||
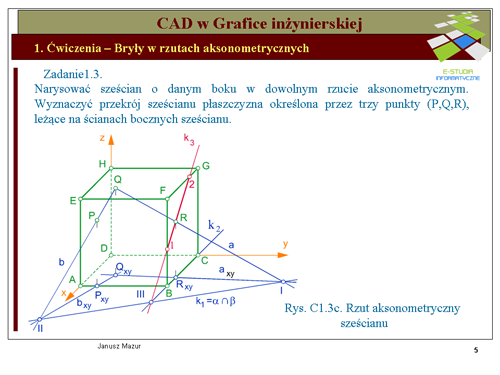
'''Wyznaczanie krawędzi <math>k_2\ | '''Wyznaczanie krawędzi <math>k_2\ </math>''' | ||
Krawędź <math>k_2\ | Krawędź <math>k_2\ </math> wyznaczymy w sposób natychmiastowy, albowiem stanowi ona wspólną krawędź ścian <math>ABCD\ </math>, oraz <math>BCFG\ </math>, sześcianu. | ||
'''Wyznaczanie krawędzi <math>k_3\ | '''Wyznaczanie krawędzi <math>k_3\ </math>''' | ||
Krawędź <math>k_2\ | Krawędź <math>k_2\ </math> przecina krawędź <math>k_1\ </math> w punkcie oznaczonym cyfrą <math>III\ </math>,. Punkt <math>III\ </math>, jest, zatem punktem '''''wspólnym trójki płaszczyzn''''' <math>\alpha\ </math>,, <math>\beta\ </math>, i <math>\gamma\ </math>,. Przez ten punkt, zgodnie z cytowanym wcześniej twierdzeniem, będzie przechodziła trzecia krawędź <math>k_3=\alpha \cap \gamma\ </math>. Drugi punkt wspólny tych płaszczyzn jest punktem <math>R\ </math>, (z założenia punkt należący do płaszczyzny <math>\alpha\ </math>, i <math>\beta\ </math>,). Punkty <math>III\ </math>, i <math>R\ </math>, wyznaczą nam poszukiwaną krawędź <math>k_3\ </math>,, która jest krawędzią przekroju płaszczyzny <math>\alpha\ </math>, z jedną ze ścian sześcianu. Krawędź <math>k_3\ </math>, przecina krawędzie sześcianu: <math>BF\ </math>, w punkcie <math>1\ </math>, oraz <math>CG\ </math>, w punkcie <math>2\ </math>,. Punkty te wyznaczają odcinek będący krawędzią przekroju ściany <math>BCGF\ </math>, sześcianu płaszczyzną <math>\alpha\ </math>,. | ||
|} | |} | ||
| Linia 84: | Linia 84: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_CW1_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:CWGI_CW1_Slajd6.png]] | ||
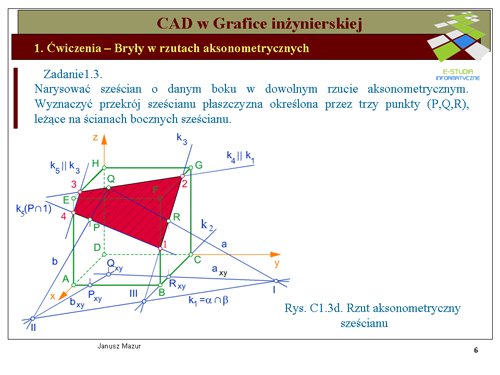
|valign="top"|Kolejne krawędzie przekroju sześcianu płaszczyzną <math>\alpha\ | |valign="top"|Kolejne krawędzie przekroju sześcianu płaszczyzną <math>\alpha\ </math>, można wyznaczyć powtarzając nasze rozumowanie, przy założeniu, że w miejsce jednej z płaszczyzn, np. <math>\gamma\ </math>, wprowadzimy kolejną płaszczyznę przechodzącą przez inną ścianę sześcianu. Możemy jednak wyznaczyć następne boki przekroju korzystając z '''''niezmienników rzutowania równoległego''''' (rys.c1.3d). | ||
Wyznaczony wcześniej punkt | Wyznaczony wcześniej punkt <math>2\ </math>, należy do krawędzi <math>k_3\ </math>,, a wiec należy do płaszczyzny <math>\alpha\ </math>,Punkt ten należy również do ściany <math>EFGH\ </math>, sześcianu. Drugim punktem wspólnym płaszczyzny <math>\alpha\ </math>, i górnej podstawy <math>EFGH\ </math>, jest punkt <math>Q\ </math>, z założenia należący do tych płaszczyzn. Zatem Kolejna krawędź <math>k_4\ </math>, będzie przechodziła przez punkty <math>Q\ </math>, i <math>2\ </math>,. Krawędź <math>k_4\ </math>,, jak wynika z niezmienników rzutowania równoległego (płaszczyzna kroi dwie równoległe do siebie płaszczyzny wzdłuż dwóch prostych równoległych) będzie równoległa do krawędzi <math>k_1\ </math>,. | ||
Kolejna krawędź <math>k_5\ | Kolejna krawędź <math>k_5\ </math>,, należąca do przekroju, będzie przechodziła przez punkt <math>3\ </math>, znajdujący się na krawędzi <math>k_4\ </math>, oraz boku <math>EH\ </math>, sześcianu. Krawędź ta będzie również równoległa do krawędzi <math>k_3\ </math>,. Zamykająca przekrój krawędź <math>k_6\ </math>, będzie przechodziła przez punkty <math>4\ </math>,, <math>P\ </math>,, i <math>1\ </math>,. | ||
|} | |} | ||
| Linia 96: | Linia 96: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_CW1_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:CWGI_CW1_Slajd7.png]] | ||
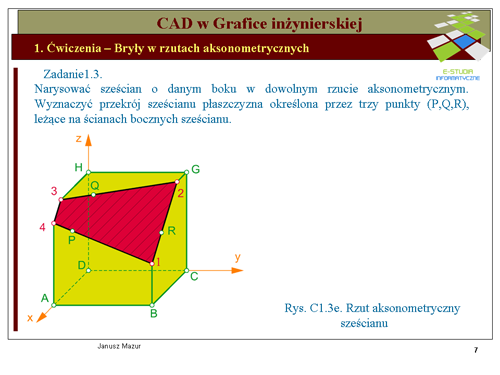
|valign="top"|Kończąc zadanie: usuwamy części krawędzi sześcianu, które zostały odcięte płaszczyzną <math>\alpha\ | |valign="top"|Kończąc zadanie: usuwamy części krawędzi sześcianu, które zostały odcięte płaszczyzną <math>\alpha\ </math>, oraz kreskujemy figurę w płaszczyźnie przekroju, zgodnie z zasadami zapisu konstrukcji. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Aktualna wersja na dzień 12:05, 5 wrz 2023
|
Kończąc zadanie: usuwamy części krawędzi sześcianu, które zostały odcięte płaszczyzną , oraz kreskujemy figurę w płaszczyźnie przekroju, zgodnie z zasadami zapisu konstrukcji. |