MN09: Różnice pomiędzy wersjami
Nie podano opisu zmian |
|||
| Linia 36: | Linia 36: | ||
[[grafika:Lagrange.jpg|thumb|right|| Lagrange<br> [[Biografia Lagrange|Zobacz biografię]]]] | [[grafika:Lagrange.jpg|thumb|right|| Lagrange<br> [[Biografia Lagrange|Zobacz biografię]]]] | ||
{{twierdzenie|Istnienie i jednoznaczność zadania interpolacji Lagrange'a|| | {{twierdzenie|Istnienie i jednoznaczność zadania interpolacji Lagrange'a|interpolacja_lagrangea| | ||
Dla dowolnej funkcji <math>\displaystyle f:D\toR</math> istnieje | Dla dowolnej funkcji <math>\displaystyle f:D\toR</math> istnieje | ||
Wersja z 14:35, 28 wrz 2006
Interpolacja wielomianowa
Zadanie interpolacji, czyli poprowadzenia krzywej zadanego rodzaju przez zestaw danych punktów, jest jednym z podstawowych zadań obliczeniowych. Stosuje się je nagminnie w najróżniejszych dziedzinach życia, np.
- Na podstawie próbki sygnału dźwiękowego (to znaczy: ciągu wartości
amplitud sygnału zmierzonych w kolejnych odstępach czasu) odtwarzanie jego przebiegu.
- Przybliżanie wykresu skomplikowanej (lub wręcz nieznanej) funkcji na
podstawie jej wartości uprzednio stablicowanych w wybranych punktach
- Interpolację stosuje się szczególnie chętnie w samej numeryce. Na przykład idea
metody siecznych polega na tym, by funkcję, której miejsca zerowego szukamy, przybliżyć prostą interpolującą tę funkcję w dwóch punktach. Metody numerycznego całkowania oraz rozwiązywania równań różniczkowych także korzystają z interpolacji.
Niech Parser nie mógł rozpoznać (nieznana funkcja „\subsetR”): {\displaystyle \displaystyle D\subsetR} i niech będzie pewnym zbiorem funkcji Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle f:D\toR} . Niech będzie ustalonym zbiorem parami różnych punktów z zwanych później węzłami.
Powiemy, że wielomian interpoluje funkcję w węzłach , gdy
Oznaczmy przez przestrzeń liniową wielomianów stopnia co najwyżej o współczynnikach rzeczywistych,
Zadanie znalezienia wielomianu interpolującego zadane wartości nazywamy zadaniem interpolacji Lagrange'a.
Zobacz biografię
Twierdzenie Istnienie i jednoznaczność zadania interpolacji Lagrange'a
Dla dowolnej funkcji Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle f:D\toR} istnieje dokładnie jeden wielomian interpolujący w węzłach , .
Dowód
Wybierzmy w dowolną bazę wielomianów , ,
Wtedy każdy wielomian z można jednoznacznie przedstawić w postaci rozwinięcia względem wybranej bazy. Warunkiem koniecznym i dostatecznym na to, aby wielomian interpolował jest spełnienie układu równań liniowych
z niewiadomymi , który w postaci macierzowej wygląda następująco:
Aby wykazać, że układ ten ma jednoznaczne rozwiązanie wystarczy, aby wektor zerowy był jedynym rozwiązaniem układu jednorodnego. Rzeczywiście, układ jednorodny odpowiada interpolacji danych zerowych, , . Istnienie niezerowego rozwiązania byłoby więc równoważne istnieniu niezerowego wielomianu stopnia nie większego od , który miałby różnych zer , co jest niemożliwe.
Zadanie znalezienia dla danej funkcji jej wielomianu interpolacyjnego stopnia co najwyżej jest więc dobrze zdefiniowane, tzn. rozwiązanie istnieje i jest wyznaczone jednoznacznie. Zauważmy, że wielomian interpolacyjny jako taki nie może być wynikiem obliczeń w naszym modelu obliczeniowym. Możemy natomiast wyznaczyć jego współczynniki w wybranej bazie.
Definicja
Niech będzie bazą w przestrzeni wielomianów stopnia co najwyżej . Zadanie interpolacji wielomianowej polega na obliczeniu dla danej funkcji współ\-czyn\-ni\-ków takich, że wielomian
interpoluje w punktach , .
Uwarunkowanie
Danymi w zadaniu interpolacji są zarówno wartości interpolowanej funkcji, jak i węzły interpolacji. Traktując węzły jako sztywno zadane parametry zadania i dopuszczając jedynie zaburzenia wartości funkcji, możemy pokazać, że jeśli zamiast rozpatrzyć jej zaburzenie , gdzie , to
gdzie
Wybór bazy wielomianowej
Jak już wiemy, zadanie interpolacji Lagrange'a sprowadza się do rozwiązania układu równań liniowych. Okazuje się, że w zależności od wyboru sposobu reprezentacji naszego wielomianu (czyli od wyboru bazy wielomianowej ), układ ten może być albo bardzo łatwy do rozwiązania, albo bardzo trudny. Co więcej, jego rozwiązanie w arytmetyce może napotykać na większe bądź mniejsze trudności (w zależności np. od uwarunkowania macierzy układu, który musimy rozwiązać).
W naturalny sposób powstaje więc problem wyboru "wygodnej" bazy w . Rozpatrzymy trzy bazy: Lagrange'a, potęgową i Newtona.
Baza Lagrange'a (kanoniczna)
Zdefiniujmy dla wielomiany
Zauważmy, że każdy z jest stopnia dokładnie oraz
Teraz widać, że wielomiany te stanowią bazę w , którą nazywamy bazą Lagrange'a. Macierz układu zadania interpolacji jest w takim wypadku identycznością i w konsekwencji , . Wielomian interpolacyjny dla funkcji można więc zapisać jako
Koszt kombinatoryczny rozwiązania zadania interpolacji jest przy tym zerowy.
Przypuśćmy, że chcielibyśmy obliczyć wartość wielomianu interpolacyjnego w punkcie różnym od , . Podstawiając
oraz mamy pierwszy wzór barycentryczny
i ostatecznie dostajemy tzw. drugi wzór barycentryczny na wielomian interpolacyjny,
gdzie . W ostatniej równości wykorzystaliśmy fakt, że , co można łatwo zobaczyć rozpatrując zadanie interpolacji funkcji . Drugi wzór barycentryczny jest korzystniejszy w implementacji.
Dla wielu układów węzłów wagi są zadane jawnymi wzorami, np. dla węzłów równoodległych (niezależnie od tego, na jakim odcinku!) wagi w drugim wzorze barycentrycznym wynoszą po prostu
Również dla Dodaj link: węzłów Czebyszewa istnieją eleganckie wzory na takie współczynnki.
Można pokazać, że wartość wielomianu iterpolacyjnego obliczona w arytmetyce według pierwszego algorytmu barycentrycznego spełnia
gdzie , a więc jest to algorytm numerycznie poprawny. Zachowanie drugiej postaci wzoru barycentrycznego w arytmetyce jest nieco bardziej skomplikowane w typowych zadaniach.
Baza potęgowa (naturalna)
Znacznie prościej można obliczyć wartość wielomianu interpolacyjnego, (a także jego pochodnych), gdy jest on dany w najczęściej używanej bazie potęgowej, , . Jeśli bowiem
to również
co sugeruje zastosowanie następującego schematu Hornera do obliczenia :
Algorytm Algorytm Hornera
<math>\displaystyle v_n = a_n;</math>
for (j=n-1; j >= 0 ; j--)
<math>\displaystyle v_j\, = \,v_{j+1}\cdot x\,+\,a_j</math>;
Po wykonaniu tego algorytmu . Schemat Hornera wymaga wykonania tylko mnożeń i dodawań. Ma on również głębszy sens, bo jego produktem ubocznym mogą być także wartości pochodnych naszego wielomianu w . Algorytm Hornera okazuje się optymalny. Każdy inny algorytm znając współczynniki wielomianu obliczający jego dokładną wartość wymaga wykonania co najmniej mnożeń i dodawań. Algorytm Hornera jest też numerycznie poprawny.
Zauważmy jednak, że w przypadku bazy potęgowej macierz układu zadania interpolacji jest pełna. Jest to tzw. macierz Vandermonde'a. Obliczenie współczynników wielomianu interpolacyjnego w bazie potęgowej bezpośrednio z tego układu stosując jedną ze znanych nam już metod kosztowałoby rzędu operacji arytmetycznych. Co gorsza, w często spotykanym przypadku, gdy węzły interpolacji są równoodległe, ta macierz jest bardzo źle uwarunkowana!
Baza Newtona
Rozwiązaniem pośrednim, które łączy prostotę obliczenia współczynników z prostotą obliczenia wartości i ewentualnie jego pochodnych, jest wybór bazy Newtona,
W tym przypadku współczynniki rozwinięcia wielomianu interpolacyjnego będziemy oznaczać przez ,
Zwróćmy od razu uwagę na ważną własność bazy Newtona. Jeśli jest wielomianem interpolacyjnym dla funkcji opartym na węzłach , , to oraz
Wartość możemy obliczyć, stosując prostą modyfikację algorytmu Hornera:
Algorytm Algorytm Hornera dla bazy Newtona
<math>\displaystyle v_n = b_n;</math>
for (j=n-1; j >= 0 ; j--)
<math>\displaystyle v_j\, = \,v_{j+1}\cdot (x-x_j)\,+\,b_j</math>;
Ponadto układ równań zadania interpolacji jest trójkątny dolny, o specyficznej strukturze, dzięki czemu można stworzyć elegancki algorytm, który teraz przedstawimy.
Algorytm różnic dzielonych
Różnicę dzieloną funkcji opartą na różnych węzłach , gdzie , definiuje się indukcyjnie jako
Zachodzi następujące ważne twierdzenie.
Twierdzenie O różnicach dzielonych
Współczynniki wielomianu interpolacyjnego Newtona dla danej funkcji dane są przez różnice dzielone w węzłach , tzn.
Dowód
Dla , oznaczmy przez wielomian z interpolujący w węzłach . Wtedy ma miejsce następująca równość ():
Aby ją pokazać, wystarczy że prawa strona tej równości, którą oznaczymy przez , przyjmuje wartości dla , . Rzeczywiście, jeśli to
Ponadto
oraz podobnie . Stąd jest wielominem z interpolującym w węzłach , , czyli .
Dalej postępujemy indukcyjnie ze względu na stopień wielomianu interpolacyjnego. Dla mamy oczywiście . Niech . Ponieważ, jak łatwo zauważyć,
z założenia indukcyjnego mamy dla . Aby pokazać podobną równość dla , zauważmy, że
Zauważmy teraz, że jest współczynnikiem przy w wielomianie . Z założenia indukcyjnego wynika, że współczynniki przy w wielomianach i są ilorazami różnicowymi opartymi odpowiednio na węzłach i . Stąd
co kończy dowód.
Różnicę dzieloną możemy łatwo obliczyć na podstawie wartości , , budując następującą tabelkę:
Zauważmy przy tym, że "po drodze" obliczamy dla wszystkich , a więc w szczególności również interesujące nas różnice dzielone . Stąd i z twierdzenia o różnicach dzielonych wynika algorytm obliczania współczynników wielomianu interpolacyjnego w bazie Newtona. Po wykonaniu następującego algorytmu,
Algorytm Metoda różnic dzielonych
for (j = 0; j <= n; j++)
<math>\displaystyle b_j</math> = <math>\displaystyle f(x_j)</math>;
for (j = 0; j <= n; j++)
for (k = n; k >= j; k--)
<math>\displaystyle b_j</math> = <math>\displaystyle (b_k-b_{k-1})/(x_k - x_{k-j})</math>;
współczynniki na końcu algorytmu zawierają wspólczynniki wielomianu interpolacyjnego w bazie Newtona. Czy gdybyś zobaczył ten algorytm na samym początku tego wykładu, zgadłbyś, do czego może służyć?!
Okazuje się, że przy realizacji w algorytmu różnic dzielonych istotną rolę odgrywa porządek węzłów. Można pokazać, że algorytm liczenia jest numerycznie poprawny ze względu na dane interpolacyjne , o ile węzły są uporządkowane nierosnąco lub niemalejąco.
Przypadek węzłów wielokrotnych
Uogólnieniem rozpatrzonego zadania interpolacji jest zadanie interpolacji Hermite'a. Zakładamy, że oprócz (różnych) węzłów dane są również ich krotności , , przy czym . Należy skonstruować wielomian taki, że
Oczywiście zakładamy przy tym, że odpowiednie pochodne funkcji istnieją.
Lemat
Zadanie interpolacji Hermite'a ma jednoznaczne rozwiązanie.
Zobacz biografię
Dowód
Istnienie i jednoznaczność rozwiązania można uzasadnić tak samo jak w przypadku węzłów jednokrotnych. Przedstawiając wielomian w dowolnej bazie otrzymujemy układ równań z niewiadomymi, który dla zerowej prawej strony ma jedynie rozwiązanie zerowe. Inaczej bowiem istniałby wielomian niezerowy stopnia nie większego niż , który miałby zera o łącznej krotności większej niż .
Nas oczywiście interesuje konstrukcja wielomianu . W tym celu ustawimy węzły w ciąg
i zdefiniujemy uogólnioną bazę Newtona w jako
Uogólnimy również pojęcie różnicy dzielonej na węzły powtarzające się, kładąc
dla , oraz
dla . Zauważmy, że przy tej definicji różnice możemy łatwo obliczyć stosując schemat podobny do tego z przypadku węzłów jednokrotnych.
Twierdzenie
Współczynniki wielomianu interpolacyjnego Hermite'a w bazie Newtona,
dane są przez odpowiednie różnice dzielone, tzn.
Dowód
Dowód przeprowadzimy podobnie jak dla węzłów jednokrotnych. Niech oznacza wielomian interpolacyjny Hermite'a oparty na (być może powtarzających się) węzłach . To znaczy, interpoluje w węzłach takich, że występuje w ciągu , a jego krotność jest liczbą powtórzeń w tym ciągu.
Zauważmy najpierw, że dla zachodzi znany nam już wzór,
Rzeczywiście, oznaczmy przez prawą stronę powyższej równości. Dla mniejszego od krotności danego węzła w ciągu , mamy , a ponieważ
to
Korzystając z tego wzoru sprawdzamy, że spełnia odpowiednie warunki interpolacyjne, a stąd .
Dalej postępujemy indukcyjnie ze względu na . Dla mamy . Dla wystarczy pokazać, że . W tym celu rozpatrzymy dwa przypadki.
Jeśli , to mamy jeden węzeł o krotności . Wielomian interpolacyjny jest wtedy postaci
a stąd . Jeśli zaś , to równość wynika z wcześniej wyprowadzonych wzorów oraz z założenia indukcyjnego.
Zauważmy, ze pojęcie różnicy dzielonej formalnie zdefiniowaliśmy jedynie dla ciągu węzłów postaci , gdzie są parami różne. Tą definicję można rozszerzyć do dowolnego ciągu węzłów. Można bowiem powiedzieć, że jest współczynnikiem przy wielomianu interpolującego w węzłach (uwzględniając krotności). Równoważnie,
Błąd interpolacji
Gdy mamy do czynienia z funkcją, która jest "skomplikowana", często dobrze jest zastąpić ją funkcją "prostszą". Mówimy wtedy o aproksymacji (przybliżaniu) funkcji. Funkcję musimy również aproksymać wtedy, gdy nie jesteśmy w stanie uzyskać pełnej o niej informacji. Na przykład, gdy funkcja reprezentuje pewien proces fizyczny, często zdarza się, że dysponujemy jedynie ciągiem próbek, czyli wartościami tej funkcji w pewnych punktach. Jasne jest, że chcielibyśmy przy tym, aby błąd aproksymacji był możliwie mały.
Z tego punktu widzenia, intepolacja wielomianowa może być traktowana jako jeden ze sposobów aproksymacji funkcji, opartym na próbkowaniu. Naturalnym staje się więc pytanie o błąd takiej aproksymacji.
Niech będą (niekoniecznie różnymi) węzłami należącymi do pewnego (być może nieskończonego) przedziału Parser nie mógł rozpoznać (nieznana funkcja „\subsetR”): {\displaystyle \displaystyle D\subsetR} . Dla danej funkcji Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle f:D\toR} , przez rozważamy, tak jak w całym wykładzie, wielomian interpolacyjny stopnia co najwyżej interpolujący w zadanych węzłach. W przypadku węzłów wielokrotnych jest to oczywiście wielomian interpolacyjny Hermite'a; gdy węzły są jednokrotne, mamy do czynienia z interpolacją Lagrange'a.
Lemat Postać błędu interpolacji
Dla dowolnego punktu błąd interpolacji w wyraża się wzorem
Jeśli ponadto , czyli pochodna w istnieje i jest ciągła, to
gdzie jest pewnym punktem należącym do najmniejszego przedziału zawierającego punkty .
Dowód
Możemy założyć, że nie jest żadnym z węzłów , . Niech będzie wielomianem interpolacyjnym funkcji opartym na węzłach i dodatkowo na węźle . Mamy wtedy
a ponieważ z warunku interpolacyjnego , to mamy też pierwszą równość w lemacie.
Aby pokazać drugą część lematu, rozpatrzmy funkcję Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle \psi:D\toR} ,
Z warunków interpolacyjnych na wynika, że funkcja ma punkty zerowe o łącznej krotności co najmniej . Wykorzystując twierdzenie Rolle'a wnioskujemy stąd, że ma zera o łącznej krotności co najmniej , ma zera o łącznej krotności co najmniej , itd. W końcu funkcja zeruje się w co najmniej jednym punkcie należącym do najmniejszego przedziału zawierającego . Wobec tego, że , a -sza pochodna wielomianu wynosi , mamy
Stąd
Zwykle interesuje nas nie tyle błąd w ustalonym punkcie , ale na całym przedziale . Zakładając teraz, że przedział jest domknięty, czyli
dla pewnych , błąd ten będziemy mierzyć w normie jednostajnej (Czebyszewa). Dla funkcji ciągłej Parser nie mógł rozpoznać (nieznana funkcja „\toR”): {\displaystyle \displaystyle g:[a,b]\toR} , norma ta jest zdefiniowana jako
Niech , gdzie , będzie klasą funkcji
gdzie . Mamy następujące twiedzenie.
Twierdzenie
Załóżmy, że każdą funkcję aproksymujemy jej wielomianem interpolacyjnym opartym na węzłach . Wtedy maksymalny błąd takiej aproksymacji wynosi
Dowód
Oszacowanie górne wynika bezpośrednio z lematu o postaci błędu interpolacji, bowiem dla mamy
Z drugiej strony zauważmy, że dla wielomianu mamy oraz
Przykład: Zjawisko Rungego
Rozważmy zadanie interpolacji funkcji
w równoodległych węzłach na przedziale . Okazuje się, że dla dużych wartości , wielomian interpolacyjny ma poważne kłopoty z aproksymacją tej funkcji przy krańcach przedziału:
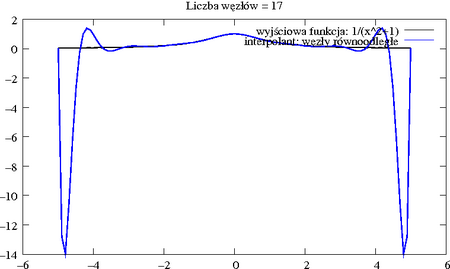
Z kolei wielomian oparty na węzłach Czebyszewa znacznie lepiej przybliża tę funkcję.
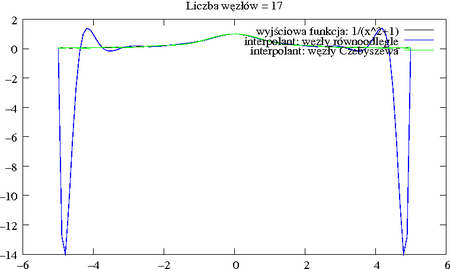
Rzeczywiście, węzły Czebyszewa zagęszczają się w pobliżu krańców odcinka.
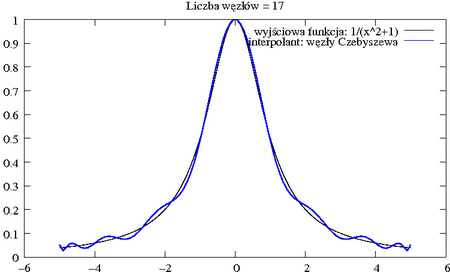
Zauważmy, że błąd aproksymacji w istotny sposób zależy od wyboru węzłów . Naturalne jest więc teraz następujące pytanie: w których punktach przedziału należy obliczać wartości funkcji, aby błąd był minimalny? Problem ten sprowadza się oczywiście do minimalizacji wielkości względem węzłów .
Twierdzenie O "optymalnym" doborze węzłów
Błąd aproksymacji w klasie funkcji jest minimalny gdy węzły interpolacji są zadane jako węzły Czebyszewa na , tzn.
Ponadto, dla optymalnych węzłów mamy
Dowód tego twierdzenia opiera się na własnościach pewnego ważnego ciągu wielomianów, który teraz przedstawimy.
Wielomiany Czebyszewa
Ciąg wielomianów Czebyszewa (pierwszego rodzaju) zdefiniowany jest indukcyjnie jako

Zobacz biografię
Zauważmy, że jest wielomianem stopnia dokładnie o współczynniku przy równym (). Ponadto wielomian można dla przedstawić w postaci
Rzeczywiście, łatwo sprawdzić, że jest to prawdą dla . Stosując podstawienie , , oraz wzór na sumę cosinusów otrzymujemy dla
co jest równoważne formule rekurencyjnej dla .

Ze wzoru wynikają również inne ważne własności wielomianów Czebyszewa. Norma wielomianu Czebyszewa na wynosi
i jest osiągana w punktach tego przedziału równych
przy czym .
W końcu, -ty wielomian Czebyszewa ma dokładnie pojedynczych zer w równych
Konsekwencją wymienionych własności jest następująca własność ekstremalna wielomianów Czebyszewa.
Przez oznaczymy klasę wielomianów stopnia o współczynniku wiodącym równym , tzn.
Twierdzenie o minimaksie
Niech . W klasie minimalną normę jednostajną na przedziale ma wielomian , tzn.
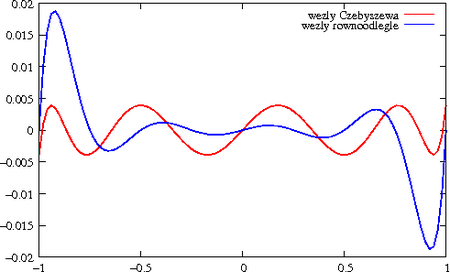
Miejsca zerowe wielomianu Czebyszewa będziemy nazywać węzłami Czebyszewa.
Dowód Twierdzenia o optymalnym doborze węzłów
Dowód wynika teraz bezpośrednio z twierdzenia o minimaksie. Zauważmy bowiem, że wielomian jest w klasie . Stąd dla optymalnymi węzłami są zera wielomianu Czebyszewa, przy których
Jeśli przedział jest inny niż , należy dokonać liniowej zamiany zmiennych tak, aby przeszedł on na . Bezpośrednie sprawdzenie pokazuje, że w klasie minimalną normę Czebyszewa na przedziale ma wielomian
Stąd
Wielomiany Czebyszewa znajdują bardzo wiele czasem zaskakujących zastosowań w różnych działach numeryki, m.in. w konstrukcji metod iteracyjnych rozwiązywania równań liniowych.
Równie interesujący jest fakt, że wielomian interpolacyjny oparty na węzłach Czebyszewa jest prawie optymalnym przybliżeniem wielomianowym zadanej funkcji:
Twierdzenie Jacksona
Dla dostatecznie gładkiej, wielomian interpolacyjny stopnia co najwyżej , oparty na węzłach Czebyszewa, spełnia
gdzie jest wielomianem stopnia co najwyżej najlepiej aproksymującym w sensie normy jednostajnej.
Jeśli więc , to wielomian oparty na węzłach Czebyszewa jest co najwyżej 3.02 razy, a gdy , maksymalnie 4 razy gorszy od optymalnego. Można więc powiedzieć, że jest prawie optymalny.