Matematyka dyskretna 1/Wykład 15: Metody algebraiczne w teorii grafów

Metody algebraiczne w teorii grafów

Graf regularny stopnia $r$ to graf, w którym wszystkie wierzchołki mają stopień $r$.
Graf taki nazywany jest także $r$-regularnym.

Maksymalny stopień wierzchołka w grafie

$\mathbf{𝐆}$

, oznaczany przez

$\mathrm{\Delta }\left(\mathbf{𝐆}\right)$

to

$\mathrm{\Delta }\left(\mathbf{𝐆}\right):=\max \{\mathsf{d}\mathsf{e}\mathsf{g}v:v\in \mathsf{V}\left(G\right)\}$.

Macierz sąsiedztwa $\mathsf{A}\left(\mathbf{𝐆}\right)$ grafu prostego $\mathbf{𝐆}=(\{v_1,\dots ,v_n\},E)$ to zero-jedynkowa macierz $⟨a_{ij}⟩$ rozmiaru $n\times n$, gdzie

$a_{ij}=\{\begin{array}{ll}1,& \text{jeżeli}{v}_i{v}_j\in E,\\ 0,& \text{w przeciwnym wypadku.}\end{array}$

Uwaga

Macierz sąsiedztwa grafu nieskierowanego jest symetryczna.

Graf prosty ${\mathbf{𝐆}}_0$ i graf skierowany ${\mathbf{𝐆}}_1$

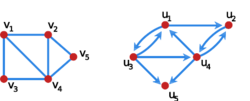
Przykład

Na rysunku Graf prosty przedstawiono graf prosty ${\mathbf{𝐆}}_0$ o wierzchołkach $v_0,\dots ,v_5$ oraz graf skierowany ${\mathbf{𝐆}}_1$ o wierzchołkach $u_1,\dots ,u_5$. Macierze sąsiędztwa grafów ${\mathbf{𝐆}}_0$ oraz ${\mathbf{𝐆}}_1$ wyglądają następująco:

$\mathsf{A}\left({\mathbf{𝐆}}_0\right)=\left[\begin{array}{ccccc}0& 1& 1& 1& 0\\ 1& 0& 0& 1& 1\\ 1& 0& 0& 1& 0\\ 1& 1& 1& 0& 1\\ 0& 1& 0& 1& 0\end{array}\right],\mathsf{A}\left({\mathbf{𝐆}}_1\right)=\left[\begin{array}{ccccc}0& 1& 1& 0& 0\\ 0& 0& 0& 1& 1\\ 1& 0& 0& 1& 1\\ 1& 1& 0& 0& 1\\ 0& 0& 0& 0& 0\end{array}\right]$

Domknięcie przechodnie grafu skierowanego $\mathbf{𝐆}$, to graf $\mathsf{T}\mathsf{C}\left(\mathbf{𝐆}\right)$ taki, że:

• $\mathsf{V}\left(\mathsf{T}\mathsf{C}\left(\mathbf{𝐆}\right)\right)=\mathsf{V}\left(\mathbf{𝐆}\right)$, oraz
• $(v,w)\in \mathsf{E}\left(\mathsf{T}\mathsf{C}\left(\mathbf{𝐆}\right)\right)$

wtedy i tylko wtedy, gdy w grafie $\mathbf{𝐆}$ istnieje skierowana marszruta z $v$ do $w$.

Twierdzenie 15.1

Niech $\mathbf{𝐆}=(\{v_1,\dots ,v_n\},E)$ będzie grafem skierowanym. Wtedy liczba skierowanych marszrut z $v_i$ do $v_j$ jest dana elementem $a_{ij}$ macierzy:

$⟨a_{ij}⟩=\mathsf{A}{\left(\mathbf{𝐆}\right)}^1+\mathsf{A}{\left(\mathbf{𝐆}\right)}^2+\dots +\mathsf{A}{\left(\mathbf{𝐆}\right)}^{(n-1)}$

Dowód

Wystarczy pokazać, że

(*) $⟨a{\text{'}}_{ij}⟩=\mathsf{A}{\left(\mathbf{𝐆}\right)}^k$ jest macierzą, w której $a{\text{'}}_{ij}$ jest liczbą skierowanych marszrut z $v_i$ do $v_j$ o długości $k$.

Dowód własności (*) przeprowadzimy indukcją względem $k$. Macierz $\mathsf{A}{\left(\mathbf{𝐆}\right)}^1$ jest macierzą sąsiedztwa, co natychmiast daje (*) dla $k=1$. Niech teraz $k>1$. Oczywiście

$\mathsf{A}{\left(\mathbf{𝐆}\right)}^k=\mathsf{A}{\left(\mathbf{𝐆}\right)}^{k-1}\cdot \mathsf{A}\left(\mathbf{𝐆}\right)$

Jeśli więc $⟨a_{ij}⟩=\mathsf{A}\left(\mathbf{𝐆}\right)$, $⟨a{\text{'}}_{ij}⟩=\mathsf{A}{\left(\mathbf{𝐆}\right)}^k$, oraz $⟨a^{\prime }{\text{'}}_{ij}⟩=\mathsf{A}{\left(\mathbf{𝐆}\right)}^{k-1}$, to

$a{\text{'}}_{ij}=a^{\prime }{\text{'}}_{i1}{a}_{1j}+\dots +a^{\prime }{\text{'}}_{in}{a}_{nj}$

Wartość $a^{\prime }{\text{'}}_{il}$ to liczba wszystkich skierowanych marszrut z $v_i$ do $v_l$ o długości $k-1$. Tak więc iloczyn $a^{\prime }{\text{'}}_{il}{a}_{lj}$ jest równy liczbie wszystkich skierowanych $k$-elementowych marszrut mających postać $v_i\to \dots \to v_l\to v_j$, czyli takich skierowanych marszrut z $v_i$ do $v_j$ o $k$ elementach, których przedostatni wierzchołek to $v_l$. Sumując te wartości po wszystkich $l$, czyli dopuszczając dowolny wierzchołek $v_l$ jako przedostatni, otrzymujemy liczbę wszystkich $k$-elementowych skierowanych marszrut z $v_i$ do $v_j$. To kończy dowód (*), a zatem i całego twierdzenia.

Load video

Local File

Local File might collect personal data.

Continue Dismiss

Graf ${\mathbf{𝐆}}_2$ (a) oraz jego przechodnie domknięcie ${\mathbf{𝐆}}_3=\mathsf{T}\mathsf{C}\left({\mathbf{𝐆}}_2\right)$ (b)

Przykład

Grafy ${\mathbf{𝐆}}_2=(\{u_1,\dots ,u_5\},E)$ i ${\mathbf{𝐆}}_3=(\{u_1,\dots ,u_5\},E^{\prime })$ zostały przedstawione na animacji.

Macierz sąsiedztwa grafu ${\mathbf{𝐆}}_2$ to

$\mathsf{A}\left({\mathbf{𝐆}}_2\right)=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1\\ 1& 0& 0& 1& 1\\ 1& 1& 0& 0& 1\\ 0& 0& 0& 0& 0\end{array}\right]$

Ponadto

$\sum _{i=1}^4\mathsf{A}{\left({\mathbf{𝐆}}_2\right)}^i=\left[\begin{array}{ccccc}1& 3& 0& 2& 3\\ 2& 3& 0& 3& 5\\ 4& 5& 0& 4& 7\\ 3& 5& 0& 3& 6\\ 0& 0& 0& 0& 0\end{array}\right]$

W macierzy $⟨a{\text{'}}_{ij}⟩=\sum _{i=1}^4\mathsf{A}{\left({\mathbf{𝐆}}_2\right)}^i$ wartość $a{\text{'}}_{ij}$ mówi o liczbie różnych skierowanych marszrut z wierzchołka $v_i$ do $v_j$ o długości co najwyżej $4$. Dla przykładu $a_{34}=4$ i rzeczywiście $u_3\to u_4$, $u_3\to u_4\to u_2\to u_4$, $u_3\to u_1\to u_2\to u_4$, i $u_3\to u_4\to u_1\to u_2\to u_4$ są wszystkimi skierowanymi marszrutami jakie można znaleźć w grafie ${\mathbf{𝐆}}_2$ prowadzące z wierzchołka $v_3$ do $v_4$ o długości co najwyżej $4$. Z kolei macierz sąsiedztwa dla przechodniego domknięcia grafu ${\mathbf{𝐆}}_2$ to

$\mathsf{A}\left(\mathsf{T}\mathsf{C}\left({\mathbf{𝐆}}_2\right)\right)=\left[\begin{array}{ccccc}0& 1& 0& 1& 1\\ 1& 0& 0& 1& 1\\ 1& 1& 0& 1& 1\\ 1& 1& 0& 0& 1\\ 0& 0& 0& 0& 0\end{array}\right]$

Warto zaobserwować oczywisty fakt, że macierz $\mathsf{A}\left(\mathsf{T}\mathsf{C}\left({\mathbf{𝐆}}_2\right)\right)$ można równie dobrze uzyskać z macierzy $\sum _{i=1}^4\mathsf{A}{\left({\mathbf{𝐆}}_2\right)}^i$ przez zamianę każdej niezerowej wartości na $1$ oraz wyzerowanie przekątnej.

Wniosek 15.2

Dla grafu $\mathbf{𝐆}$ o wierzchołkach $v_1,\dots ,v_n$ i macierzy $⟨a_{ij}⟩=\mathsf{A}{\left(\mathbf{𝐆}\right)}^1+\mathsf{A}{\left(\mathbf{𝐆}\right)}^2+\dots +\mathsf{A}{\left(\mathbf{𝐆}\right)}^{(n-1)}$, jeśli tylko $i\ne j$, to

$a_{ij}>0\text{wtedy i tylko wtedy, gdy}(v_i,v_j)\in \mathsf{E}\left(\mathsf{T}\mathsf{C}\left(\mathbf{𝐆}\right)\right)$

Macierz incydencji $\mathsf{B}\left(\mathbf{𝐆}\right)$ grafu $\mathbf{𝐆}=(\{v_1,\dots ,v_n\},\{e_1,\dots ,e_m\})$ to zero-jedynkowa macierz $⟨b_{ij}⟩$ rozmiaru $n\times m$, gdzie

$b_{ij}=\{\begin{array}{ll}1,& \text{jeśli wierzchołek}{v}_i\text{jest incydentny z krawędzią}{e}_j,\\ 0,& \text{w przeciwnym wypadku.}\end{array}$

Zorientowana macierz incydencji $\mathsf{C}\left(\mathbf{𝐆}\right)$ grafu prostego to macierz $⟨c_{ij}⟩$, rozmiaru $n\times m$, otrzymana z macierzy incydencji $\mathsf{B}\left(\mathbf{𝐆}\right)$ poprzez zastąpienie w każdej kolumnie jednej z dwu jedynek przez $-1$(minus jeden).

Graf prosty ${\mathbf{𝐆}}_4$

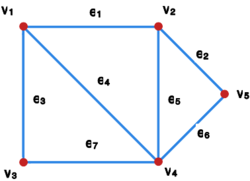
Przykład

Dla grafu ${\mathbf{𝐆}}_4=(\{v_1,\dots ,v_5\},\{e_1,\dots ,e_7\})$ przedstawionego na rysunku Graf prosty G4 macierz incydencji oraz zorientowana macierz incydencji, to odpowiednio:

$\mathsf{B}\left({\mathbf{𝐆}}_4\right)=\left[\begin{array}{ccccccc}1& 0& 1& 1& 0& 0& 0\\ 1& 1& 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 1& 1\\ 0& 1& 0& 0& 0& 1& 0\end{array}\right],$

$\mathsf{C}\left({\mathbf{𝐆}}_4\right)=\left[\begin{array}{ccccccc}-1& 0& 1& -1& 0& 0& 0\\ 1& -1& 0& 0& 1& 0& 0\\ 0& 0& -1& 0& 0& 0& -1\\ 0& 0& 0& 1& -1& -1& 1\\ 0& 1& 0& 0& 0& 1& 0\end{array}\right]$

Obserwacja 15.3

• Dla macierzy incydencji $⟨b_{ij}⟩$ oraz zorientowanej macierzy incydencji $⟨c_{ij}⟩=\mathsf{C}\left(\mathbf{𝐆}\right)$ zachodzi $b_{ij}=\left|c_{ij}\right|\text{dla}i=1,\dots ,n\text{oraz}j=1,\dots ,m$.
• W zorientowanej macierzy incydencji $⟨c_{ij}⟩$ mamy: $c_{1j}+\dots +c_{nj}=0\text{dla}j=1,\dots ,m$.

Macierz stopni $\mathsf{D}\left(\mathbf{𝐆}\right)$ grafu prostego $\mathbf{𝐆}=(\{v_1,\dots ,v_n\},E)$ to diagonalna macierz $⟨d_{ij}⟩$ rozmiaru $n\times n$, gdzie

$d_{ij}=\{\begin{array}{ll}\mathsf{d}\mathsf{e}\mathsf{g}{v}_i,& \text{jeżeli}i=j,\\ 0,& \text{w przeciwnym wypadku.}\end{array}$

Przykład

Dla grafu ${\mathbf{𝐆}}_4$ przedstawionego na rysunku Graf prosty G4 odpowiednia macierz stopni to

$\mathsf{D}\left({\mathbf{𝐆}}_4\right)=\left[\begin{array}{ccccc}3& 0& 0& 0& 0\\ 0& 3& 0& 0& 0\\ 0& 0& 2& 0& 0\\ 0& 0& 0& 4& 0\\ 0& 0& 0& 0& 2\end{array}\right]$

Twierdzenie 15.4

Jeśli $\mathbf{𝐆}=(V,E)$ jest grafem prostym, to

$\mathsf{B}\left(\mathbf{𝐆}\right)\cdot \mathsf{B}{\left(\mathbf{𝐆}\right)}^T=\mathsf{D}\left(\mathbf{𝐆}\right)+\mathsf{A}\left(\mathbf{𝐆}\right)$,

gdzie $\mathsf{B}{\left(\mathbf{𝐆}\right)}^T$ jest macierzą transponowaną macierzy $\mathsf{B}\left(\mathbf{𝐆}\right)$.

Przykład

Policzmy macierze opisane w Twierdzeniu 15.4 dla grafu ${\mathbf{𝐆}}_4$ z rysunku Graf prosty G4. Tak więc

$\begin{array}{rlr}\mathsf{B}\left({\mathbf{𝐆}}_4\right)\cdot \mathsf{B}{\left({\mathbf{𝐆}}_4\right)}^T& =& \left[\begin{array}{ccccccc}1& 0& 1& 1& 0& 0& 0\\ 1& 1& 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 1& 1\\ 0& 1& 0& 0& 0& 1& 0\end{array}\right]\cdot \left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 0& 1& 0& 0& 1\\ 1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 0& 1& 0& 1& 0\\ 0& 0& 0& 1& 1\\ 0& 0& 1& 1& 0\end{array}\right]\\ & =& \left[\begin{array}{ccccc}3& 1& 1& 1& 0\\ 1& 3& 0& 1& 1\\ 1& 0& 2& 1& 0\\ 1& 1& 1& 4& 1\\ 0& 1& 0& 1& 2\end{array}\right]=\mathsf{D}\left({\mathbf{𝐆}}_4\right)+\mathsf{A}\left({\mathbf{𝐆}}_4\right).\end{array}$

Dowód [Twierdzenia 15.4]

Niech $m_{ij}$ będzie elementem w $i$-tym wierszu oraz w $j$-tej kolumnie macierzy $M=\mathsf{B}\left(\mathbf{𝐆}\right)\cdot \mathsf{B}{\left(\mathbf{𝐆}\right)}^T$. Z definicji $M$ wynika, że

$m_{ij}=b_{i1}\cdot b_{j1}+\dots +b_{i\left|E\right|}\cdot b_{j\left|E\right|}$

Rozważmy dwa przypadki:

• $i\ne j$. Wtedy $b_{ik}\cdot b_{jk}=1$ jest równoważne temu, że krawędź $e_k$ łączy wierzchołek $v_i$ z $v_j$. Tak więc $m_{ij}=1$ wtedy i tylko wtedy, gdy $v_i$ sąsiaduje z $v_j$.
• $i=j$. Wtedy $b_{ik}\cdot b_{jk}=1$ jest równoważne temu, że krawędź $e_k$ jest incydentna z $v_i$. Sumując wartości $b_{ik}\cdot b_{ik}$ dla $k=1,\dots ,\left|E\right|$ uzyskujemy liczbę krawędzi incydentnych do $v_i$, czyli stopień $\mathsf{d}\mathsf{e}\mathsf{g}{v}_i$.

Twierdzenie 15.5

Niech $\mathbf{𝐆}$ będzie grafem skierowanym o $n$ wierzchołkach, a macierz $M$ o rozmiarach $(n-1)\times (n-1)$, będzie minorem (podmacierzą) zorientowanej macierzy incydencji $\mathsf{C}\left(\mathbf{𝐆}\right)$, w którym kolumny odpowiadają krawędziom z pewnego podzbioru $\mathsf{E}\left(M\right)$ zbioru $\mathsf{E}\left(\mathbf{𝐆}\right)$. Wtedy

$\mathbf{𝐇}=(\mathsf{V}\left(\mathbf{𝐆}\right),\mathsf{E}\left(M\right))$jest drzewem wtedy i tylko wtedy, gdy $M$ jest nieosobliwa.

Przykładowe drzewo $\mathbf{𝐇}$ wraz z zaznaczoną ścieżką $P_i$

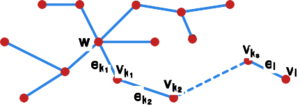
Dowód

Niech $w$ będzie wierzchołkiem odpowiadającym jedynemu wierszowi pominiętemu w minorze $M$.

Niech $\mathbf{𝐇}=(\mathsf{V}\left(\mathbf{𝐆}\right),\mathsf{E}\left(M\right))$ będzie drzewem. Dla pokazania, że wtedy macierz $M$ jest nieosobliwa, dokonamy takiej permutacji wierszy i kolumn macierzy $M$, by uzyskana w ten sposób macierz $M^{\prime }=⟨m{\text{'}}_{ij}⟩$ była trójkątna i miała wyłącznie niezerowe elementy na przekątnej. Zostanie to uzyskane przez takie ponumerowanie wierzchołków i krawędzi grafu $\mathbf{𝐇}$, by w nowej macierzy

$m{\text{'}}_{ij}\ne 0$ wtedy i tylko wtedy, gdy wierzchołek $v_i$ jest incydentny z $e_j$.

Przypomnijmy, że odległość pomiędzy dwoma wierzchołkami $x$ i $y$ w grafie to liczność najkrótszej ścieżki od $x$ do $y$. Ponumerujmy wierzchołki z $\mathsf{V}\left(\mathbf{𝐆}\right)$ w taki sposób, że jeśli $v_i$ jest bliżej wierzchołka $w$, niż $v_j$ to $i\le j$. Numeracji takich może być wiele, ale dla nas nie ma znaczenia, którą z nich wybierzemy i ustalimy dla dalszej części dowodu. Zauważmy jedynie, że w każdej takiej numeracji wierzchołek $w$ znajduje się na początku. Ponieważ graf $\mathbf{𝐇}$ jest drzewem, to między wierzchołkiem $w$ i dowolnym $v_i$ istnieje dokładnie jedna ścieżka. Oznaczmy ją przez $P_i=w\to v_{k_1}\to \dots \to v_{k_s}\to v_i$. Oczywiście, dla $i\ne j$ ostanie krawędzie w ścieżkach $P_i$ i $P_j$ są różne. Tę ostatnią krawędź ścieżki $P_i$ oznaczmy, tak jak na rysunku, indeksem $i$, czyli $e_i=v_{k_s}{v}_i$.

Ponieważ w drzewie $\mathbf{𝐇}$ jest dokładnie $n-1$ krawędzi, przypisanie wierzchołkowi $v_i$ krawędzi $e_i$ jest bijekcją między $\mathsf{V}\left(\mathbf{𝐆}\right)-\left\{w\right\}$ a $\mathsf{E}\left(\mathbf{𝐇}\right)$. W kolumnie $j_0$ macierzy $M$, odpowiadającej krawędzi $e_{j_0}=v_{j_1}{v}_{j_0}$, są jedynie dwa niezerowe elementy - jeden leży w wierszu $j_0$, odpowiadającemu wierzchołkowi $v_{j_0}$, a drugi w wierszu $j_1$. Skoro krawędź $e_{j_0}$ ma ten sam numer co wierzchołek $v_{j_0}$, wierzchołek $v_{j_1}$ musi leżeć na ścieżce z $w$ do $v_{j_0}$. Tym samym $v_{j_1}$ jest bliżej $w$ niż $v_{j_0}$, a zatem $j_1<j_0$. Macierz $M^{\prime }$ jest więc macierzą trójkątną górną z niezerową przekątną, co kończy dowód.

Załóżmy teraz, że $\mathbf{𝐇}$ nie jest drzewem. Ponieważ $\mathbf{𝐇}$ ma jedynie $n-1$ krawędzi, to zależność miedzy liczbą wierzchołków, krawędzi i składowych spójnych daje, że $\mathbf{𝐇}$ ma co najmniej $2$ składowe. Niech wierzchołki $v_{i_1},\dots ,v_{i_l}$ tworzą składową, w której nie występuje $w$. Jeżeli, w $i_p$-tym wierszu i $r$-tej kolumnie macierzy $M$ jest niezerowy element $x=\pm 1$, to wierzchołek $v_{i_p}$ jest incydentny z krawędzią $e_r=v_{i_p}{v}_{i_s}$. Wierzchołek $v_{i_s}$ będący drugim końcem krawędzi $e_r$ leży oczywiście w tej samej składowej co $v_{i_p}$, a zatem macierz $M$ ma liczbę $-x$ w $r$-tej kolumnie i w $i_s$-tym wierszu. Sumując teraz wiersze macierzy $M$ o indeksach $i_1,\dots ,i_l$ otrzymujemy wektor zerowy. To oczywiście oznacza, że macierz $M$ jest osobliwa.

Wniosek 15.6

W spójnym grafie prostym $\mathbf{𝐆}$ o $n$ wierzchołkach rząd macierzy $\mathsf{C}\left(\mathbf{𝐆}\right)$ wynosi $n-1$.

Wielomian charakterystyczny grafu $\mathbf{𝐆}$ to wielomian charakterystyczny macierzy sąsiedztwa $\mathsf{A}\left(\mathbf{𝐆}\right)$.

Permanent grafu $\mathbf{𝐆}$ to permanent macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$, czyli

$\mathsf{p}\mathsf{e}\mathsf{r}\mathsf{A}\left(\mathbf{𝐆}\right)=\sum _{\sigma }{a}_{1,\sigma (1)}\cdot a_{2,\sigma (2)}\cdot \dots \cdot a_{n,\sigma (n)}$,

gdzie suma $\sum _{\sigma }$ rozciąga się po wszystkich permutacjach $\sigma$, zaś $a_{ij}$ oznacza element macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$.

Wyznacznik grafu $\mathbf{𝐆}$ to wyznacznik macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$, czyli

$\mathsf{d}\mathsf{e}\mathsf{t}\mathsf{A}\left(\mathbf{𝐆}\right)=\sum _{\sigma }(-1{)}^{\mathsf{s}\mathsf{g}\mathsf{n}(\sigma )}{a}_{1,\sigma (1)}\cdot a_{2,\sigma (2)}\cdot \dots \cdot a_{n,\sigma (n)}$.

Skojarzenie niedoskonałe (a) i doskonałe (b)

Algebraiczne pojęcie permanentu macierzy okazuje się użytecznym przy badaniu skojarzeń w grafie. Rozważaliśmy już skojarzenia w grafach dwudzielnych.

Skojarzenie w grafie $\mathbf{𝐆}=(V,E)$ to taki podzbiór $M\subseteq E$, że żadne jego dwie krawędzie nie są incydentne z tym samym wierzchołkiem.

Skojarzenie doskonałe to skojarzenie wykorzystujące wszystkie wierzchołki grafu.

Twierdzenie 15.7

Prosty graf dwudzielny $\mathbf{𝐆}=(V_1\cup V_2,E)$ ma skojarzenie doskonałe wtedy i tylko wtedy, gdy $\mathbf{𝐆}$ ma niezerowy permanent.

Dowód

Niech $⟨a_{ij}⟩=\mathsf{A}\left(\mathbf{𝐆}\right)$. Dowód ma dwa etapy. Najpierw pokażemy, że:

1. Permanent grafu $\mathbf{𝐆}$ jest niezerowy wtedy i tylko wtedy, gdy istnieje permutacja ${\rho }_0$ liczb $1,\dots ,n$ taka, że $a_{i{\rho }_0\left(i\right)}=1$ dla $i=1,\dots ,n$.

Istotnie, każdy składnik sumy dającej permanent grafu $\mathbf{𝐆}$

$\mathsf{p}\mathsf{e}\mathsf{r}\mathsf{A}\left(\mathbf{𝐆}\right)=\sum _{\sigma }{a}_{1,\sigma (1)}\cdot a_{2,\sigma (2)}\cdot \dots \cdot a_{n,\sigma (n)}$

jest zawsze nieujemny. A zatem cała suma będzie dodatnia wtedy i tylko wtedy, gdy choć jeden jej składnik będzie niezerowy. To z kolei jest równoważne temu, że dla choć jednej permutacji ${\rho }_0$ zachodzi

$a_{i{\rho }_0\left(i\right)}=1$

dla wszystkich $i=1,\dots ,n$.

2. Graf $\mathbf{𝐆}$ ma doskonałe skojarzenie $M\subseteq E$ wtedy i tylko wtedy, gdy istnieje permutacja ${\rho }_0$ liczb $1,\dots ,n$ taka, że $a_{i{\rho }_0\left(i\right)}=1$ dla $i=1,\dots ,n$.

Istotnie, w skojarzeniu doskonałym każdy wierzchołek jest incydentny z dokładnie jedną krawędzią. A zatem skojarzenie $M$ wyznacza permutację ${\rho }_0$ poprzez

${\rho }_0\left(i\right)=j\text{wtedy i tylko wtedy, gdy }{v}_i{v}_j\in M$

Nadto $a_{i{\rho }_0\left(i\right)}=1$ dla wszystkich $i=1,\dots ,n$.

Z drugiej strony, jeśli $(i_1,\dots ,i_k)$ jest cyklem permutacji ${\rho }_0$, tzn.

${\rho }_0\left(i_1\right)=i_2,{\rho }_0\left(i_2\right)=i_3,\dots ,{\rho }_0\left(i_{k-1}\right)=i_k,{\rho }_0\left(i_k\right)=i_1$,

to założona równość $a_{i{\rho }_0\left(i\right)}=1$ mówi, że cyklowi temu odpowiada cykl $v_{i_1}\to v_{i_2}\to \dots \to v_{i_k}\to v_{i_1}$ w grafie $\mathbf{𝐆}$. Oczywiście w grafie dwudzielnym cykl taki musi mieć parzystą liczbę wierzchołków, tak więc zbiór krawędzi

$\{v_{i_1}{v}_{i_2},v_{i_3}{v}_{i_4},\dots ,v_{i_{k-1}}{v}_{i_k}\}$

tworzy doskonałe skojarzenie zbioru wierzchołków $\{v_{i_1},v_{i_2},v_{i_3},\dots v_{i_{k-1}},v_{i_k}\}$. Po zsumowaniu skojarzeń odpowidającym wszystkim cyklom permutacji ${\rho }_0$ otrzymamy skojarzenie doskonałe w grafie $\mathbf{𝐆}$.

Graf ${\mathbf{𝐆}}_5$

Skojarzenie doskonałe w grafie ${\mathbf{𝐆}}_5$

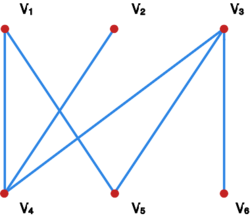
{{przyklad||| Rozważmy graf ${\mathbf{𝐆}}_5=(\{v_1,v_2,v_3,v_4,v_5,v_6\},E)$ przedstawiony na rysunku Graf G5.

Macierz sąsiedztwa $\mathsf{A}\left({\mathbf{𝐆}}_5\right)$ to

$\mathsf{A}\left({\mathbf{𝐆}}_5\right)=\left[\begin{array}{cccccc}0& 0& 0& 1& 1& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 1& 1& 1& 0& 0& 0\\ 1& 0& 1& 0& 0& 0\\ 1& 1& 1& 0& 0& 0\end{array}\right]$

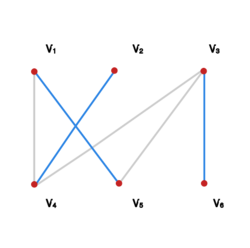
Permanent $\mathsf{p}\mathsf{e}\mathsf{r}{\mathbf{𝐆}}_5=1$, tak więc istnieje skojarzenie doskonałe $M$. Jedno z takich skojarzeń, przedstawione na rysunku Skojarzenie doskonałe w grafie G5, odpowiada wyróżnionym elementom macierzy:

$\mathsf{A}\left({\mathbf{𝐆}}_5\right)=\left[\begin{array}{cccccc}0& 0& 0& 1& \underset{\_}{\mathbf{1}}& 0\\ 0& 0& 0& \underset{\_}{\mathbf{1}}& 0& 0\\ 0& 0& 0& 1& 1& \underset{\_}{\mathbf{1}}\\ 1& \underset{\_}{\mathbf{1}}& 1& 0& 0& 0\\ \underset{\_}{\mathbf{1}}& 0& 1& 0& 0& 0\\ 0& 0& \underset{\_}{\mathbf{1}}& 0& 0& 0\end{array}\right]$

Przy badaniu kolorowań grafów przydatne okazuje się inne pojęcie algebraiczne.

Wartość własna grafu $\mathbf{𝐆}$ to wartość własna macierzy sąsiedztwa $\mathsf{A}\left(\mathbf{𝐆}\right)$.

Obserwacja 15.8

Macierz sąsiedztwa $\mathsf{A}\left(\mathbf{𝐆}\right)$ jest rzeczywista i symetryczna, zatem wszystkie jej wartości własne są rzeczywiste i istnieje baza ortogonalna złożona z jej wektorów własnych.

Dla grafu prostego $\mathbf{𝐆}$ przyjmujemy oznaczenia:

• ${\lambda }_{max}\left(\mathbf{𝐆}\right)$ na maksymalną wartość własną macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$,
• ${\lambda }_{min}\left(\mathbf{𝐆}\right)$ na minimalną wartość własną macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$.

Obserwacja 15.9

Wartości własne grafu $\mathbf{𝐆}$ są, co do wartości bezwzględnej, nie większe niż maksymalny stopień wierzchołków grafu $\mathbf{𝐆}$, tzn.

$\left|{\lambda }_{max}\left(\mathbf{𝐆}\right)\right|\le \mathrm{\Delta }\left(\mathbf{𝐆}\right)$

Dowód

Niech $\left|\mathbf{𝐆}\right|=n$ oraz $x=⟨x_1,\dots ,x_n⟩$ będzie niezerowym wektorem własnym macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)=⟨a_{ij}⟩$ o wartości własnej ${\lambda }_{max}\left(\mathbf{𝐆}\right)$. Bez straty ogólności można założyć, że $\left|x_k\right|=\underset{i=1,\dots ,n}{\max }\left|x_i\right|=1$. Oszacowanie modułu $k$-tej współrzędnej wektora $\mathsf{A}\left(\mathbf{𝐆}\right)\cdot x={\lambda }_{max}\left(\mathbf{𝐆}\right)\cdot x$ daje nierówność:

$\begin{array}{rl}\left|{\lambda }_{max}\left(\mathbf{𝐆}\right)\right|& =\left|{\lambda }_{max}\left(\mathbf{𝐆}\right)x_k\right|\\ & =|a_{k1}{x}_1+\dots +a_{kn}{x}_n|\\ & \le & a_{k1}\left|x_1\right|+\dots +a_{kn}\left|x_n\right|\\ & \le a_{k1}+\dots +a_{kn}\\ & =\mathsf{d}\mathsf{e}\mathsf{g}{x}_k\le \mathrm{\Delta }\left(\mathbf{𝐆}\right).\end{array}$

Dowód następnych dwu obserwacji pozostawiamy jako ćwicznia 4 i 6.

Obserwacja 15.10

W grafie prostym $\mathbf{𝐆}$ mamy ${\lambda }_{max}\left(\mathbf{𝐆}\right)=\mathrm{\Delta }\left(\mathbf{𝐆}\right)$ wtedy i tylko wtedy, gdy któraś spójna składowa grafu $\mathbf{𝐆}$ jest grafem regularnym stopnia $\mathrm{\Delta }\left(\mathbf{𝐆}\right)$.

Obserwacja 15.11

W spójnym grafie prostym $\mathbf{𝐆}$ liczba $-\mathrm{\Delta }\left(\mathbf{𝐆}\right)$ jest wartością własną macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$ wtedy i tylko wtedy, gdy $\mathbf{𝐆}$ jest regularnym grafem dwudzielnym stopnia $\mathrm{\Delta }\left(\mathbf{𝐆}\right)$.

Twierdzenie 15.12 [wzór Hoffman'a]

W grafie regularnym $\mathbf{𝐆}$ stopnia $r$ zachodzi

$\alpha \left(\mathbf{𝐆}\right)\le \frac{\left|\mathsf{V}\left(\mathbf{𝐆}\right)\right|\cdot {\lambda }_{min}\left(\mathbf{𝐆}\right)}{{\lambda }_{min}\left(\mathbf{𝐆}\right)-r}$,

gdzie $\alpha \left(\mathbf{𝐆}\right)$ oznacza największy możliwy rozmiar indukowanej antykliki w grafie $\mathbf{𝐆}$.

Dowód

Niech $n=\left|\mathsf{V}\left(\mathbf{𝐆}\right)\right|$ oraz

$U:=\mathsf{A}\left(\mathbf{𝐆}\right)-{\lambda }_{min}\left(\mathbf{𝐆}\right)\cdot I-(r-{\lambda }_{min}\left(\mathbf{𝐆}\right))\cdot n^{-1}\cdot J$,

gdzie $I$ jest macierzą diagonalną rozmiaru $n\times n$, która na przekątnej ma jedynki, a $J$ jest macierzą rozmiaru $n\times n$ w całości wypełnioną jedynkami. Ponadto niech wektor $x=⟨x_i⟩$ będzie funkcją charakterystyczną najliczniejszego zbioru niezależnego $X\subseteq \mathsf{V}\left(\mathbf{𝐆}\right)$takiego, że $\mathbf{𝐆}{|}_X$ jest antykliką. Oznacza to, że

$x_i=\{\begin{array}{ll}1,& \text{jeśli}{v}_i\in X,\\ 0,& \text{w przeciwnym wypadku.}\end{array}$

Wtedy $y=\mathsf{A}\left(\mathbf{𝐆}\right)\cdot x$ jest funkcją charakterystyczną zbioru sąsiadów wierzchołków w $X$, czyli

$y_i=\{\begin{array}{ll}1,& \text{jeśli}{v}_i\notin X,\\ 0,& \text{w przeciwnym wypadku.}\end{array}$

To z kolei daje, że

$x^T\cdot \mathsf{A}\left(\mathbf{𝐆}\right)\cdot x=x^T\cdot y=0$

i w konsekwencji

$x^T\cdot U\cdot x=-{\lambda }_{min}\left(\mathbf{𝐆}\right)\cdot \left|x\right|-(r-{\lambda }_{min}\left(\mathbf{𝐆}\right))\cdot n^{-1}\cdot {\left|x\right|}^2$

Uzasadnimy teraz, że $x^T\cdot U\cdot x\ge 0$. Dla $j={[1,1,\dots ,1]}^T$ mamy:

$U\cdot j=r\cdot j-{\lambda }_{min}\left(\mathbf{𝐆}\right)\cdot j-(r-{\lambda }_{min}\left(\mathbf{𝐆}\right))\cdot j=0$

Z kolej każdy inny wektor własny $z$ macierzy $\mathsf{A}\left(\mathbf{𝐆}\right)$ o wartości własnej $\lambda$, który jest prostopadły do $j$ spełnia

$U\cdot z=(\lambda -{\lambda }_{min}\left(\mathbf{𝐆}\right))\cdot z$,

przy czym oczywiście $\lambda -{\lambda }_{min}\left(\mathbf{𝐆}\right)\ge 0$. Oznacza to, że wszystkie wartości własne macierzy $U$ są nieujemne. Niech więc $u_1,\dots ,u_n$ będzie ortogonalną bazą złożoną z wektorów własnych macierzy $U$, a ${\lambda }_1,\dots ,{\lambda }_n$ będą odpowiadającymi im wartościami własnymi. Niech ponadto $x=b_1\cdot u_1+\dots +b_n\cdot u_n$ będzie rozkładem wektora $x$ w tej bazie. Wtedy:

$\begin{array}{rl}{x}^T\cdot U\cdot x& =x^T\cdot (b_1\cdot {\lambda }_1\cdot u_1+\dots +b_n\cdot {\lambda }_n\cdot u_n)\\ & =b_1^2\cdot {\lambda }_1+\dots +b_n^2\cdot {\lambda }_n\ge 0.\end{array}$

W konsekwencji

$0\le -{\lambda }_{min}\left(\mathbf{𝐆}\right)\cdot \left|x\right|-(r-{\lambda }_{min}\left(\mathbf{𝐆}\right))\cdot n^{-1}\cdot {\left|x\right|}^2$.

Ponieważ $\left|x\right|=\alpha \left(\mathbf{𝐆}\right)$ a $n=\left|\mathsf{V}\left(\mathbf{𝐆}\right)\right|$, to ta ostatnia jest innym zapisem dowodzonej nierówności.

Wniosek 15.13

W regularnym grafie $\mathbf{𝐆}$ zachodzi

$\chi \left(\mathbf{𝐆}\right)\ge 1-\frac{{\lambda }_{max}\left(\mathbf{𝐆}\right)}{{\lambda }_{min}\left(\mathbf{𝐆}\right)}$

Dowód

Ponieważ podział zbioru wierzchołków $\mathsf{V}\left(\mathbf{𝐆}\right)$ na rozłączne podzbiory $V_1,\dots ,V_k$ indukujące antykliki, jest równoważny z kolorowaniem grafu $\mathbf{𝐆}$ przy użyciu $k$ kolorów, to

$\left|\mathsf{V}\left(\mathbf{𝐆}\right)\right|\le \chi \left(\mathbf{𝐆}\right)\cdot \alpha \left(\mathbf{𝐆}\right)$

Jeśli teraz $r$ jest stopniem regularności grafu $\mathbf{𝐆}$ to Twierdzenie 15.12 daje więc

$\chi \left(\mathbf{𝐆}\right)\ge \frac{{\lambda }_{min}\left(\mathbf{𝐆}\right)-r}{{\lambda }_{min}\left(\mathbf{𝐆}\right)}$

Ponieważ graf $\mathbf{𝐆}$ jest $r$-regularny, to na mocy Obserwacji 15.10 mamy $r={\lambda }_{max}\left(\mathbf{𝐆}\right)$, co pozwala zakończyć dowód.