Języki, automaty i obliczenia/Wykład 11: Automat ze stosem

Automat ze stosem

W tym wykładzie określimy automat ze stosem rozpoznający języki bezkontekstowe. Wprowadzimy dwie definicje rozpoznawania języków przez automat ze stosem oraz omówimy ważną podklasę języków bezkontekstowych, mianowicie języków rozpoznawanych przez deterministyczne automaty ze stosem. Uzasadnimy też fakt, iż rodzina języków rozpoznawana przez automaty ze stosem pokrywa się z rodziną jezyków bezkontekstowych.

Automaty ze stosem to systemy rozpoznające języki bezkontekstowe. Ich działanie jest nieco bardziej skomplikowane niż działanie automatu skończenie stanowego. Poza możliwością zmiany stanu pod wpływem czytanego symbolu umieszczonego na taśmie wejściowej automat ten posiada także taśmę stosu, na którą może wpisywać słowa, jak i odczytywać pojedynczy symbol znajdujący się na wierzchu stosu.

Definicja 1.1

Automatem ze stosem nad alfabetem $A$ nazywamy system $𝒜 𝒮 = (A, A_{S}, Q, f, s_{0}, z_{0}, Q_{F})$ , w którym:

$A$ - jest alfabetem,

$A_{S}$ - jest dowolnym skończonym i niepustym zbiorem zwanym alfabetem stosu (niekoniecznie rozłącznym z $A$ ),

$Q$ - jest dowolnym, skończonym i niepustym zbiorem zwanym zbiorem stanów,

$f : A_{S} \times Q \times (A \cup {1}) ⟶ 𝒫_{s k} (A_{S}^{*} \times Q)$ jest funkcją przejść, której wartościami są skończone podzbiory $A_{S}^{*} \times Q$ (także zbiór pusty),

$q_{0} \in Q$ jest stanem początkowym,

$z_{0} \in A_{S}$ symbolem początkowym stosu,

$Q_{F} \subset Q$ zbiorem stanów końcowych.

Badając działanie automatu ze stosem, wygodniej jest, zamiast funkcji przejść $f$ , rozważać skończoną relację $P \subset (A_{S} \times Q \times (A \cup {1})) \times (A_{S}^{*} \times Q)$ zwaną relacją przejść. Elementy tej relacji nazywane są prawami. Relacja $P$ jest zatem skończonym zbiorem praw o następującej postaci:

$z q_{i} ⟶ u q_{j}$ dla $z \in A_{S}, u \in A_{S}^{*}, q_{i}, q_{j} \in Q$ ,
$z q_{i} a ⟶ u q_{j}$ dla $z \in A_{S}, u \in A_{S}^{*}, a \in A, q_{i}, q_{j} \in Q$ .

Często, używając relacji przejść, oznaczamy automat ze stosem jako układ:

𝒜 𝒮 = (A, A_{S}, Q, P, s_{0}, z_{0}, Q_{F})

.

Prawo $z q_{i} a ⟶ u q_{j}$ będziemy reprezentować grafem:

Napis $z / u$ oznacza, iż symbol $z$ pobrany ze stosu wymieniany jest na słowo $u$ utworzone nad alfabetem stosu $A_{S}$ .

Natomiast prawo $z q_{i} \to u q_{j}$ interpretowane jest graficznie jako:

Działanie automatu ze stosem $𝒜 𝒮$ zależne jest, jak wspomnieliśmy we wstępie wykładu, nie tylko od czytanego przez automat słowa, ale także od symbolu znajdującego się na wierzchu stosu. Poniżej przedstawiamy graficznie te zależności.

Animacja 1

Prawo $z q_{i} a ⟶ u q_{j}$ dla słowa $u = z_{1} \dots z_{m}$ określające działanie automatu $𝒜 𝒮$ interpretujemy w ten sposób, że automat, będąc w stanie $q_{i}$ po przeczytaniu litery $a$ (ze słowa wejściowego) i symbolu $z$ ze stosu, zmienia stan na $q_{j}$ oraz zastępuje na stosie literę $z$ słowem $u$ w ten sposób, że ostatnia litera tego słowa, symbol $z_{m}$ , jest na wierzchu stosu. Ten właśnie symbol będzie pobrany ze stosu przy kolejnym "ruchu" automatu, zgodnie z zasadą last in, first out. Ilustruje tę zasadę animacja, która jest zamieszczona będzie w dalszej części tego wykładu.

Dla precyzyjnego opisu działania automatu ze stosem wprowadza się pojęcie konfiguracji automatu, poprzedzając to pojęcie określeniem konfiguracji wewnętrznej.

Definicja 1.2

Konfiguracją wewnętrzną automatu ze stosem $A S$ nazywamy dowolną parę $(u, q) \in A_{S}^{*} \times Q$ taką, że $q$ jest stanem, w którym automat znajduje się aktualnie, a $u$ słowem zapisanym na stosie tak, że litera będąca na wierzchu stosu jest ostatnią literą tego słowa.

Konfiguracją automatu ze stosem $A S$ nazywamy trójkę

(u, q, w) \in A_{S}^{*} \times Q \times A^{*}

gdzie $(u, q)$ jest konfiguracją wewnętrzną, a $w$ słowem wejściowym.

Wprowadzone pojęcia wykorzystamy do określenia działania automatu ze stosem dla dowolnych słów wejściowych i dowolnych słów znajdujących się na stosie. W tym celu rozszerzymy odpowiednio relację przejść $P$ , określając ją na zbiorze konfiguracji i oznaczając symbolem $| ⟹$ . Przyjmujemy dla dowolnych słów $u_{1}, u_{2} \in A_{S}^{*}$ i litery $z \in A_{S}$ , dla dowolnego słowa $w \in A^{*}$ i $a \in A \cup {1}$ oraz dla dowolnych stanów $q_{1}, q_{2} \in Q$ , że zachodzi relacja

(u_{1} z, q_{1}, a w) | ⟹ (u_{1} u_{2}, q_{2}, w)

wtedy i tylko wtedy, gdy $z q_{1} a ⟶ u_{2} q_{2} \in P$ .

Zwrotne i przechodnie domknięcie tej relacji nazywamy przejściem lub poprawnym obliczeniem automatu $A S$ i oznaczamy symbolem $| ⟹^{*}$ .

Dla dowolnego słowa $w \in A^{*}$ przyjmujemy oznaczenie $(u, q) ∣ ⟹^{w} (u_{1}, q_{1})$ , jeśli ma miejsce $(u, q, w) | ⟹^{*} (u_{1}, q_{1}, 1)$ . Prawdziwa jest wówczas następująca równość:

\begin{array}{c} | ⟹^{w_{1}} \circ \end{array} \begin{array}{c} | ⟹^{w_{2}} : = \end{array} \begin{array}{c} | ⟹^{w_{1} w_{2}} \end{array}

Mówimy, że konfiguracja wewnętrzna $(u, q)$ automatu ze stosem $A S$ jest osiągalna z konfiguracji wewnętrznej $(u_{1}, q_{1})$ , jeśli istnieje takie słowo $w \in A^{*}$ , że

(u_{1}, q_{1}) ∣ ⟹^{w} (u, q)

.

Zdefiniujemy teraz język rozpoznawany przez automat ze stosem. W literaturze spotkać można kilka równoważnych definicji rozpoznawania. W naszym wykładzie wprowadzimy dwie, używane najczęściej:

rozpoznawanie poprzez stany końcowe (wyróżniony zbiór stanów końcowych $Q_{F}$ ),
rozpoznawanie poprzez pusty stos.

Definicja 1.3

Niech $𝒜 𝒮 = (A, A_{S}, Q, P, s_{0}, z_{0}, Q_{F})$ będzie automatem ze stosem. Językiem rozpoznawanym przez automat $𝒜 𝒮$ poprzez stany końcowe nazywamy zbiór

L_{F} (𝒜 𝒮) = {w \in A^{*} : (z_{0}, q_{0}) ∣ ⟹^{w} (u, q_{F}), : u \in A_{S}^{*}, q_{F} \in Q_{F}} .

Językiem rozpoznawanym przez automat $𝒜 𝒮$ poprzez pusty stos nazywamy zbiór

L_{e} (𝒜 𝒮) = {w \in A^{*} : (z_{0}, q_{0}) ∣ ⟹^{w} (1, q), q \in Q}

.

Używając drugiego określenia rozpoznawania, w definicji automatu ze stosem pomija się zbiór stanów końcowych $Q_{F}$ .

Przykład 1.1

Poniższa animacja ilustruje działanie automatu ze stosem. Przedstawiony grafem automat ze stosem $𝒜 𝒮 = (A, A_{S}, {q_{0}, q_{F}}, P, q_{0}, z_{0}, {q_{F}})$ , w którym alfabet stosu $A_{S} = {z_{0}, a, b}$ rozpoznaje język bezkontekstowy

L (𝒜 𝒮) = {w \in {a, b}^{*} : #_{a} w = #_{b} w}

.

Animacja 2

Zauważmy, że automat ten rozpoznaje ten sam język zarówno zarówno przez stany końcowe ( $Q_{F} = {q_{F}}$ ), jak i w sensie rozpoznawania przez pusty stos.

W ogólności dla ustalonego automatu ze stosem $𝒜 𝒮$ wprowadzone wyżej dwa sposoby rozpoznawania niekoniecznie prowadzą do tego samego języka. Jednak są one równoważne, o czym przekonuje następujące twierdzenie, w dowodzie którego konstruujemy odpowiednie automaty ze stosem.

Twierdzenie 1.1

Język $L \subset A^{*}$ jest rozpoznawany przez automat ze stosem przez stany końcowe wtedy i tylko wtedy, gdy jest rozpoznawany przez automat ze stosem poprzez pusty stos.

Dowód

Załóżmy, że automat $𝒜 𝒮 = (A, A_{S}, Q, P, s_{0}, z_{0}, Q_{F})$ rozpoznaje przez stany końcowe język $L = L_{F} (𝒜 𝒮)$ . Wówczas automat

{𝒜 𝒮}^{'} = (A, A_{S} \cup {x_{0}}, Q \cup {q_{0^{'}}, q_{e}}, P^{'}, q_{0^{'}}, x_{0})

,

w którym symbol $x_{0}$ jest spoza alfabetu $A_{S}$ , stany $q_{0^{'}}, q_{e}$ nie należą do $Q$ , a relacja przejść $P^{'}$ określona jest poniżej

\begin{array}{lll} P^{'} = & P : : \cup & {x_{0} q_{0^{'}} ⟶ x_{0} z_{0} q_{0}, \\ z q ⟶ q_{e}, : q \in Q_{F}, z \in A_{s} \cup {x_{0}}, \\ z q_{e} ⟶ q_{e}, : z \in A_{S} \cup {x_{0}}}, \end{array}

rozpoznaje język $L$ przez pusty stos.

Na odwrót, jeśli automat ze stosem $𝒜 𝒮 = (A, A_{S}, Q, P, q_{0}, z_{0})$ rozpoznaje poprzez pusty stos język $L = L_{e} (𝒜 𝒮)$ , to automat

{𝒜 𝒮}^{'} = (A, A_{S} \cup {x_{0}}, Q \cup {q_{0^{'}}, q_{F}}, P^{'}, q_{0^{'}}, x_{0}, {q_{F}})

,

w którym symbol $x_{0}$ jest spoza alfabetu $A_{S}$ , stany $q_{0^{'}}, q_{F}$ nie należą do $Q$ , a relacja przejść $P^{'}$ określona jest poniżej

P^{'} = P \cup {x_{0} q_{0^{'}} ⟶ x_{0} z_{0} q_{0}, x_{0} q ⟶ q_{F}, q \in Q}

rozpoznaje język $L$ poprzez stany końcowe.

Zdefiniujemy i omówimy teraz deterministyczne automaty ze stosem. W odróżnieniu od automatów skończenie stanowych deterministyczne automaty ze stosem posiadają mniejsze możliwości rozpoznawania języków niż automaty, które dopuszczają przejścia niedeterministyczne.

Definicja 1.4

Automat ze stosem $𝒜 𝒮 = (A, A_{S}, Q, f, s_{0}, z_{0}, Q_{F})$ nazywamy deterministycznym, jeśli dla każdej konfiguracji $(z, q, a) \in A_{S} \times Q \times (A \cup {1})$ wartość funkcji $f (z, q, a)$ jest zbiorem co najwyżej jednoelementowym, czyli $♯ f (z, q, a) ⩽ 1$ oraz jeśli $f (z, q, 1) \neq \emptyset$ , to $f (z, q, a) = \emptyset$ dla każdego $a \in A$ .

A więc deterministyczny automat ze stosem ma możliwość co najwyżej jednego przejścia z dowolnej konfiguracji $(z, q, a) \in A_{S} \times Q \times (A \cup {1})$ oraz jeśli istnieje przejście dla określonego stanu i symbolu ze stosu pod wpływem słowa pustego, to jest ono jedynym możliwym dla tego układu w tym automacie.

Język rozpoznawany przez deterministyczny automat ze stosem nazywamy językiem deterministycznym.

O tym, że, w przeciwieństwie do klasy języków regularnych, języki rozpoznawane przez deterministyczne automaty ze stosem stanowią właściwą podklasę wszystkich języków akceptowanych przez automaty ze stosem, przekonuje przykład.

Przykład 1.2

Język $L = {a^{n} b^{n} : : n ⩾ 1} \cup {a^{n} b^{2 n} : : n ⩾ 1}$ rozpoznawany przez automat ze stosem opisany grafem

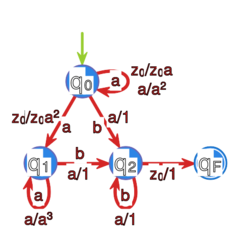
nie jest językiem deterministycznym. Zauważmy bowiem, że deterministyczny automat ze stosem, aby zaakceptować słowo $a^{n} b^{n}$ , dla kontrolowania ilości liter $a$ i $b$ wykorzystuje stos, wprowadzając przy czytaniu każdej litery $a$ ustalony symbol na stos, na przykład $a$ i usuwając sekwencyjnie te symbole przy czytaniu liter $b$ . Dla zaakceptowania słowa $a^{n} b^{2 n}$ podobne postępowanie prowadzi do wpisywania na stos słowa $a a$ z alfabetu stosu dla każdej litery $a$ i usuwaniu pojedynczego symbolu przy czytaniu $b$ . Jest to jedyny sposób kontroli ilości liter, a opisane działanie automatu jest źródłem jego istotnej niedeterministyczności. Bez trudu można zauważyć, że każdy automat ze stosem rozpoznający język $L$ będzie zawierać ten niedeterministyczny układ w swojej strukturze.

Aby lepiej uchwycić istotę tego niedeterminizmu, zauważmy, że automat ze stosem określony grafem

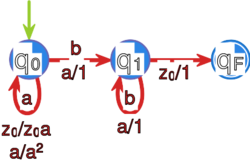
rozpoznaje język $L = {a^{n} b^{n} : : n ⩾ 1}$ i jest deterministyczny.

Każdy język rozpoznawany przez deterministyczny automat ze stosem jest oczywiście (dlaczego?) jednoznaczny. Jednoznaczność języka nie implikuje jednak jego deterministyczności, o czym przekonuje zamieszczony poniżej przykład.

Przykład 1.3

Język $L = {a^{n} b^{n} : : n ⩾ 1} \cup {a^{n} b^{2 n} : : n ⩾ 1}$ , który jest rozpoznawany przez automat ze stosem z poprzedniego przykładu, nie jest, jak wiemy, deterministyczny, ale jest jednoznaczny.

Gramatyki bezkontekstowe i automaty ze stosem

Automaty ze stosem charakteryzują rodzinę języków bezkontekstowych w tym samym sensie, w jakim automaty skończenie stanowe charakteryzują języki regularne.

Twierdzenie 2.1

Rodzina języków rozpoznawanych przez automaty ze stosem jest równa rodzinie języków bezkontekstowych $ℒ_{2}$ .

Dowód

(szkic)

Dla dowodu, że każdy język bezkontekstowy jest rozpoznawany przez odpowiedni automat ze stosem, rozważmy gramatykę $G = (V_{N}, V_{T}, v_{0}, P_{G})$ bezkontekstową w postaci normalnej Greibach i załóżmy, że słowo puste $1$ nie należy do języka $L (G)$ generowanego przez tę gramatykę. Podamy konstrukcję automatu ze stosem $A S$ , który, jak można wykazać, akceptuje poprzez pusty stos język $L (G)$ . Niech

𝒜 𝒮 = (V_{T}, V_{N} \cup V_{T}, {q}, f, q, v_{0})

,

gdzie funkcja $f : (V_{N} \cup V_{T}) \times {q} \times (V_{T} \cup {1}) ⟶ 𝒫_{s k} ((V_{N} \cup V_{T})^{*} \times {q})$ określona jest następująco. Dla dowolnych $v \in V_{N}, : a \in V_{T}$

f (v, q, 1) = {(\overset{\leftarrow}{x} a, q) : : : v \to a x \in P_{G}}

f (a, q, a) = {(1, q)}

oraz ma wartość równą zbiorowi pustemu $\emptyset$ we wszystkich pozostałych przypadkach.

Jest to więc automat o jednym stanie $q$ , alfabetem wejściowym jest alfabet terminalny $V_{T}$ , alfabetem stosu jest suma mnogościowa alfabetu symboli nieterminalnych $V_{N}$ i terminalnych $V_{T}$ , a symbol początkowy stosu jest symbolem startowym gramatyki. Istotą działania automatu $A S$ jest symulacja lewostronnego wyprowadzenia w gramatyce $G .$ Pełne uzasadnienie podanej konstrukcji znajduje sie na końcu tego wykładu, w części "dla zainteresowanych".

Załóżmy teraz, że automat $𝒜 𝒮 = (A, A_{S}, Q, f, q_{0}, z_{0})$ akceptuje poprzez pusty stos język $L (𝒜 𝒮)$ . Konstrukcja gramatyki bezkontekstowej $G$ , która generuje ten sam język przebiega następująco. Niech $G = ((Q \times A_{S} \times Q) \cup {v_{0}}, A, v_{0}, P_{G})$ , gdzie $v_{0} \notin Q \cup A_{S} \cup A$ . Wprowadzamy do zbioru praw $P_{G}$ wyłącznie następujące prawa:

$v_{0} \to (q_{0}, z_{0}, q)$ dla wszystkich stanów $q \in Q$ ,
$(q, z, q_{1}) \to a (q_{k + 1}, z_{k}, q_{k}) (q_{k}, z_{k - 1}, q_{k - 1}) \dots (q_{2}, z_{1}, q_{1})$ dla dowolnych stanów $q, q_{1}, \dots, q_{k + 1} \in Q, a \in A \cup {1}, z, z_{1}, \dots z_{k} \in A_{S}$ jeśli $(z_{1} . . . z_{k}, q_{k + 1}) \in f (z, q, a)$ ,
$(q, z, q_{1}) \to a \in P_{G}$ jeśli $(1, q_{1}) \in f (z, q, a)$ .

Mamy więc następującą równoważność:

$(1)$

\begin{array}{c} \begin{array}{c} (q, z, q_{1}) \to a (q_{k + 1}, z_{k}, q_{k}) (q_{k}, z_{k - 1}, q_{k - 1}) \dots (q_{2}, z_{1}, q_{1}) \in P_{G} \end{array} \\ \begin{array}{c} \Leftrightarrow (z_{1} \dots z_{k}, q_{k + 1}) \in f (z, q, a), \end{array} \end{array}

która w szczególności dla $k = 0$ przyjmuje postać

(q, z, q_{1}) \to a \in P_{G} \Leftrightarrow (1, q_{1}) \in f (z, q, a)

i oznacza dla gramatyki wymazywanie symboli nieterminalnych, a dla automatu wymazywanie symboli stosu.

Skonstruowana gramatyka $G$ odtwarza działanie automatu $A S$ działającego pod wpływem słowa wejściowego $w$ . Pełne uzasadnienie podanej konstrukcji znajduje się na końcu tego wykładu, w części "dla zainteresowanych".

Z konstrukcji przedstawionej w szkicu dowodu twierdzenia wynika, że każdy język bezkontekstowy może być rozpoznawany poprzez pusty stos przez automat ze stosem o jednym stanie. Określenie algorytmów na podstawie powyższego twierdzenia proponujemy jako ćwiczenie.

Powróćmy na moment do języka Łukasiewicza. Język ten oraz jego gramatyka zostały wprowadzone podczas pierwszego wykładu poświęconego językom bezkontekstowym. Każde słowo, generowane przez tę gramatykę, jest pewnym wyrażeniem algebraicznym zapisanym w notacji polskiej, prefiksowej, bez użycia nawiasów. Bez trudności można określić gramatykę bezkontekstową, która generuje język Łukasiewicza, w którym słowa zapisywane są w wersji postfiksowej. Wystarczy bowiem przyjąć: $G = (V_{N}, V_{T}, v_{0}, P)$ , gdzie $V_{N} = {v_{0}}$ , $V_{T} = {a, b, +, *}$ , $v_{0} = v$ oraz $P = {v \to a, v \to b, v \to v v +, v \to v v *}$ . Język Łukasiewicza jest więc teraz zbiorem

L (G) = {a, : b, a b +, b a b + *, a b + a b + *, \dots} .

Oczywiście język ten jest rozpoznawany przez odpowiedni automat ze stosem. Określeniem takiego automatu zajmiemy się podczas ćwiczeń. Warto zauważyć, że rozpoznając słowa języka Łukasiewicza w postfiksowej postaci, automat ze stosem działa dokładnie tak, jak obliczane są wartości wyrażeń arytmetycznych we współczesnych procesorach. Automat ze stosem, czytając wyrażenie od lewej do prawej, zapisuje wyniki częściowe na stosie, a operacje wykonywane są zawsze na ostatnich elementach stosu.

Dla bardziej dociekliwych studentów proponujemy poniżej pełny dowód twierdzenia 2.1 orzekajacego, że języki rozpoznawane przez automaty ze stosem to dokładnie języki bezkontekstowe.

Dla zainteresowanych

Dowod

Dla dowodu, że każdy język bezkontekstowy jest rozpoznawany przez odpowiedni automat ze stosem, rozważmy gramatykę $G = (V_{N}, V_{T}, v_{0}, P_{G})$ bezkontekstową, w postaci normalnej Greibach i załóżmy, że słowo puste $1$ nie należy do języka $L (G)$ generowanego przez tę gramatykę. Konstruujemy teraz automat ze stosem $A S$ , który, jak udowodnimy, akceptuje poprzez pusty stos język $L (G)$ . Niech

𝒜 𝒮 = (V_{T}, V_{N} \cup V_{T}, {q}, f, q, v_{0})

gdzie funkcja $f : (V_{N} \cup V_{T}) \times {q} \times (V_{T} \cup {1}) ⟶ 𝒫_{s k} ((V_{N} \cup V_{T})^{*} \times {q})$ określona jest następujaco. Dla dowolnych $v \in V_{N}, : a \in V_{T}$

f (v, q, 1) = {(\overset{\leftarrow}{x} a, q) : : : v \to a x \in P_{G}}

f (a, q, a) = {(1, q)}

oraz równa jest zbiorowi pustemu $\emptyset$ we wszystkich pozostałych przypadkach.

A zatem jest to automat o jednym stanie $q$ , alfabetem wejściowym jest alfabet terminalny $V_{T}$ , alfabetem stosu jest suma mnogościowa alfabetu symboli nieterminalnych $V_{N}$ i terminalnych $V_{T}$ , a symbol początkowy stosu jest symbolem startowym gramatyki. Działanie automatu $A S$ symuluje lewostronne wyprowadzenie w gramatyce $G .$

Dla dowolnego słowa $w \in L (G)$ istnieje lewostronne wyprowadzenie

v_{0} \mapsto a_{1} v_{1} y_{1} \mapsto a_{1} a_{2} v_{2} y_{2} \mapsto . . . \mapsto a_{1} . . . a_{k - 1} v_{k - 1} \mapsto a_{1} . . . a_{k} = w

gdzie $a_{i} \in V_{T}$ , $v_{i} \in V_{N}$ oraz $y_{i} \in V_{N}^{*}$ , gdyż gramatyka jest w postaci Greibach. Odpowiada temu wyprowadzeniu następujące działanie automatu $𝒜 𝒮$ :

(v_{0}, q) ∣ ⟹^{1} (\overset{\leftarrow}{y_{1}} v_{1} a_{1}, q) ∣ ⟹^{a_{1}} (\overset{\leftarrow}{y_{1}} v_{1}, q) ∣ ⟹^{1} (\overset{\leftarrow}{y_{2}} v_{2} a_{2}, q) ∣ ⟹^{a_{2}} . .

.

. . . ∣ ⟹^{1} (v_{k - 1} a_{k - 1}, q) ∣ ⟹^{a_{k - 1}} (v_{k - 1}, q) ∣ ⟹^{1} (a_{k}, q) ∣ ⟹^{a_{k}} (1, q)

.

A to oznacza zaakceptowanie słowa $w$ poprzez pusty stos. Zatem $L (G) \subset L (𝒜 𝒮)$ . Dla dowodu inkluzji w przeciwną stronę wykorzystamy implikację

(v_{0}, q) ∣ ⟹^{w} (\overset{\leftarrow}{x}, q) w 𝒜 𝒮 ⟹ v_{0} \mapsto_{L}^{*} w x w G

która ma miejsce dla dowolnego $w \in V_{T}^{*}$ . Implikację tę udowodnimy indukcyjnie ze względu na długość słowa $w$ . Dla słowa pustego $1$ oraz dla $w = a \in V_{T}$ powyższa implikacja wynika bezpośrednio z definicji automatu ze stosem. Załóżmy teraz, że $(v_{0}, q) ∣ ⟹^{w} (\overset{\leftarrow}{x}, q)$ w $𝒜 𝒮$ i niech $w = w_{1} a$ dla $a \in V_{T}$ i $w_{1} \in V_{T}^{*}$ . Mamy więc $(v_{0}, q) ∣ ⟹^{w_{1}} (\overset{\leftarrow}{y}, q)$ i $(\overset{\leftarrow}{y}, q) ∣ ⟹^{a} (\overset{\leftarrow}{x}, q)$ w automacie $𝒜 𝒮$ . Z założenia indukcyjnego wnioskujemy, że $v_{0} \mapsto_{L}^{*} w_{1} y$ w $G$ . W przypadku, gdy $y = a$ , wnioskujemy z określenia automatu ze stosem, że $x = 1$ i wtedy $v_{0} \mapsto_{L}^{*} w_{1} a = w$ w $G$ . Jeśli natomiast $y = v y^{'}$ dla $v \in V_{N}$ i $y^{'} \in V_{N}^{*}$ , to w automacie $𝒜 𝒮$ ma miejsce wyprowadzenie

(v_{0}, q) ∣ ⟹^{w_{1}} (\overset{\leftarrow}{y}, q) = (\overset{\leftarrow}{y^{'}} v, q) ∣ ⟹^{1} (\overset{\leftarrow}{y^{'}} \overset{\leftarrow}{x^{'},} q) ∣ ⟹^{a} (\overset{\leftarrow}{x}, q)

gdzie $x^{'} = a z, a \in V_{T}$ i $z \in V_{N}^{*}$ i prawo $v \to x^{'} \in P_{G}$ . W dalszym ciągu działania automatu następuje krok $(\overset{\leftarrow}{y^{'}} \overset{\leftarrow}{x^{'},} q) ∣ ⟹^{a} (\overset{\leftarrow}{x}, q)$ , a to w konsekwencji oznacza, że w gramatyce $G$ ma miejsce wyprowadzenie

v_{0} \mapsto_{L}^{*} w_{1} y = w_{1} v y^{'} \mapsto_{L}^{*} w_{1} x^{'} y^{″} \mapsto_{L}^{*} w_{1} a z y^{'} = w x .

Załóżmy teraz, że automat $𝒜 𝒮 = (A, A_{S}, Q, f, q_{0}, z_{0})$ rozpoznaje z pustym stosem język $L (𝒜 𝒮)$ . Skonstruujemy gramatykę bezkontekstową $G$ , generującą ten sam język. Niech $G = ((Q \times A_{S} \times Q) \cup {v_{0}}, A, v_{0}, P_{G})$ , gdzie $v_{0} \notin Q \cup A_{S} \cup A$ . Do zbioru praw $P_{G}$ zaliczymy wyłącznie następujące prawa:

$v_{0} \to (q_{0}, z_{0}, q)$ dla wszystkich stanów $q \in Q$ ,
$(q, z, q_{1}) \to a (q_{k + 1}, z_{k}, q_{k}) (q_{k}, z_{k - 1}, q_{k - 1}) \dots (q_{2}, z_{1}, q_{1})$ dla dowolnych stanów $q, q_{1}, \dots, q_{k + 1} \in Q, a \in A \cup {1}, z, z_{1}, \dots z_{k} \in A_{S}$ jeśli $(z_{1} . . . z_{k}, q_{k + 1}) \in f (z, q, a)$ ,
$(q, z, q_{1}) \to a \in P_{G}$ jeśli $(1, q_{1}) \in f (z, q, a)$ .

Mamy więc następującą równoważność:

$(2)$

\begin{array}{c} \begin{array}{c} (q, z, q_{1}) \to a (q_{k + 1}, z_{k}, q_{k}) (q_{k}, z_{k - 1}, q_{k - 1}) \dots (q_{2}, z_{1}, q_{1}) \in P_{G} \end{array} \\ \begin{array}{c} \Leftrightarrow (z_{1} \dots z_{k}, q_{k + 1}) \in f (z, q, a), \end{array} \end{array}

która w szczególności dla $k = 0$ przyjmuje postać

(q, z, q_{1}) \to a \in P_{G} \Leftrightarrow (1, q_{1}) \in f (z, q, a)

i oznacza dla gramatyki wymazywanie symboli nieterminalnych, a dla automatu wymazywanie symboli stosu.

Skonstruowana gramatyka $G$ odtwarza działanie automatu $A S$ działającego pod wpływem słowa wejściowego $w$ co udowodnimy poniżej. W tym celu wykażemy indukcyjnie ze względu na długość słowa $w \in A^{*}$ następującą równoważność:

\begin{array}{c} (q, z, q_{1}) \mapsto_{G}^{*} w (q_{k + 1}, z_{k}, q_{k}) \dots (q_{2}, z_{1}, q_{1}) \Leftrightarrow \\ \Leftrightarrow (z, q) ∣ ⟹^{w} (z_{1} \dots z_{k}, q_{k + 1}) . \end{array}

Dla $w = a \in A$ równoważność redukuje się do obserwacji (2). Załóżmy teraz, że słowo $w = w_{1} a$ oraz że w gramatyce $G$ mamy wyprowadzenie $(q, z, q_{1}) \Rightarrow_{G}^{*} w_{1} a (q_{k + 1}, z_{k}, q_{k}) \dots (q_{2}, z_{1}, q_{1})$ . Z postaci gramatyki $G$ wynika, że to wyprowadzenie można przedstawić nastepująco:

\begin{array}{c} (q, z, q_{1}) \mapsto_{G}^{*} w_{1} (q^{'}, z^{'}, q_{p}) (q_{p}, z_{p - 1}, q_{p - 1}) \dots (q_{2}, z_{1}, q_{1}) \\ \mapsto_{G} w_{1} a (q_{k + 1}, z_{k}, q_{k}) \dots (q_{p + 1}, z_{p}, q_{p}) (q_{p}, z_{p - 1}, q_{p - 1}) \dots (q_{2}, z_{1}, q_{1}) . \end{array}

dla pewnego $p ⩽ k$ i odpowiednich $q, q^{'}, q_{1}, \dots, q_{k + 1} \in Q, z, z^{'}, z_{1}, \dots z_{k} \in A_{S}$ .

Z założenia indukcyjnego wynika, iż pierwszy fragment wyprowadzenia jest w automacie $A S$ zastąpiony równoważnie poprawnym obliczeniem

(z, q) ∣ ⟹^{w_{1}} (z_{1} \dots z_{p - 1} z^{'}, q^{'})

,

a drugi

(z_{1} \dots z_{p - 1} z^{'}, q^{'}) | ⟹^{a} (z_{1} \dots z_{p - 1} z_{p} . . . z_{k}, q_{k + 1})

.

A to oznacza, że w automacie $A S$ mamy poprawne obliczenie

(z, q) ∣ ⟹^{w_{1} a} (z_{1}, \dots z_{k}, q_{k + 1})

,

co kończy dowód indukcyjny równoważności. Na jej podstawie, przyjmując $q = q_{0}, : z = z_{0}$ , otrzymujemy:

(q_{0}, z_{0}, q) \mapsto_{G}^{*} w \Leftrightarrow (z_{0}, q_{0}) ∣ ⟹^{w} (1, q^{'})

.

Uwzględniając, iż dla dowolnego stanu $q$ mamy w gramatyce $G$ prawo $v_{0} \to (q_{0}, z_{0}, q)$ oraz że automat $A S$ akceptuje słowa przez pusty stos (stan $q^{'}$ jest nieistotny), ostatnia równoważność kończy dowód twierdzenia.

Języki, automaty i obliczenia/Wykład 11: Automat ze stosem

Spis treści

Automat ze stosem

Gramatyki bezkontekstowe i automaty ze stosem

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia