Matematyka dyskretna 1/Wykład 4: Sumy skończone i rachunek różnicowy

Wstęp

Oto dwie konwencje zapisu skończonych sum wyrazów:

$a_1+a_2+\dots +a_n=\sum _{i=1}^n{a}_i$

Czasami stosowana jest ogólniejsza notacja $\sum _{i\in I}{a}_i$, gdzie $I$ jest skończonym zbiorem indeksów. Jeśli $I$ jest pusty to suma ma
wartość $0$.

Często, zamiast określać zbiór indeksów $I$ podaje się pod sumą warunek ten zbiór definiujący. Na przykład:

$\sum _{\begin{array}{c}1\le i\le n\\ i\text{ nieparzysta}\end{array}}{a}_i$

Częstym zadaniem wobec którego stajemy to sprowadzenie sumy do postaci zwartej lub choćby znacząco prostszej. Ten wykład zawiera krótki przegląd metod i strategii obliczania skończonych sum. Znakomita część wykładu poświęcona jest prezentacji rachunku różnicowego - narzędzia pozwalającego liczyć skończone sumy w sposób systematyczny.

Kilka metod obliczania skończonych sum

Odgadnięcie rozwiązania i udowodnienie go przez indukcję

W wykładach o indukcji i rekurencji analizowaliśmy kilka przykładów tą metodą. Analogicznie rozwiązywaliśmy też równania rekursywne. Indukcja sprawdza się gdy intuicje odnośnie sumy, którą chcemy policzyć, pozwalają nam na wysuwanie hipotez co do jej wartości. Jest to też dobra metoda sprawdzenia wyników (w celu wychwycenia ewentualnych błędów) otrzymanych inną metodą. Niestety, najczęściej gdy chcemy wskazać wzór na sumę, nie jesteśmy w stanie go zgadnąć. Wtedy trzeba posłużyć się innymi metodami.

Przeindeksowanie sumy

MD1-3.1.swf

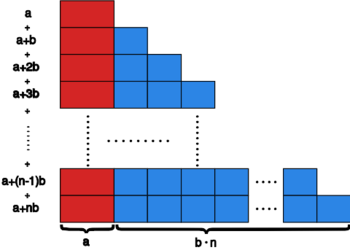
Przykład

Rozważmy sumę skończonego ciągu arytmetycznego o parametrach $a,b\in \mathbb{\mathbb{Z}}$:

$\sum _{0\le k\le n}(a+kb)=a+(a+b)+(a+2b)+(a+3b)+\dots +(a+nb)=?$

Zauważmy, że

$\sum _{0\le k\le n}(a+kb)=\sum _{0\le k\le n}(a+(n-k)b)=\sum _{0\le k\le n}(a+nb-kb)$

Carl Friedrich Gauss (1777-1855)
Zobacz biografię

Dodając odpowiednie równości stronami otrzymujemy:

$\begin{array}{rl}2\sum _{0\le k\le n}(a+kb)& =\sum _{0\le k\le n}((a+kb)+(a+nb-kb))\\ & =\sum _{0\le k\le n}(2a+nb)\\ & =(2a+nb)\sum _{0\le k\le n}1\\ & =(2a+nb)(n+1).\end{array}$

Zatem $\sum _{0\le k\le n}(a+kb)=(a+\frac{1}{2}nb)(n+1)$, czyli obliczana suma jest średnią arytmetyczną pierwszego $a$ i ostatniego $a+bn$ składnika sumy pomnożoną przez liczbę składników sumy.

Takiej metody użył młody Gauss, gdy zniecierpliwiony jego pytaniami nauczyciel polecił mu policzyć sumę tysiąca pierwszych liczb naturalnych.

Zmiana kolejności sumowania w sumach wielokrotnych

Przykład

Ciąg harmoniczny $H_n=\sum _{i=1}^n\frac{1}{i}$ poznaliśmy w wykładzie o indukcji. Pokazaliśmy tam, że

$\frac{\lfloor \lg n\rfloor +1}{2}\le H_n\le \lfloor \lg n\rfloor +1$

Tym razem jesteśmy zainteresowani sumami postaci

$\sum _{i=1}^n{H}_i=\sum _{i=1}^n\sum _{j=1}^i\frac{1}{j}$,

których pierwsze wartości przedstawia tabela:

$\begin{array}{ccccc}n& 1& 2& 3& \dots \\ H_n& 1& \frac{3}{2}& \frac{5}{3}& \dots \\ \sum _{i=0}^n{H}_i& 1& \frac{5}{2}& \frac{25}{6}& \dots \end{array}$

W tym przypadku zamienimy kolejność wyrazów w sumie po czym okaże się, że nowa postać jest prosta do przeliczenia. Wypiszmy więc wszystkie wyrazy w naszej podwójnej sumie, tak by kolejne wiersze były składnikami liczb harmonicznych:

$\begin{array}{c}1\\ 1& \frac{1}{2}\\ 1& \frac{1}{2}& \frac{1}{3}\\ \dots & \dots & \dots & \dots \\ 1& \frac{1}{2}& \frac{1}{3}& \dots & \frac{1}{n}\end{array}$

Zauważmy, że oryginalny zapis nakazuje najpierw sumować wiersze, a później wartości tych wierszy. Zmieńmy zatem kolejność sumowania aby najpierw sumować kolumny:

$\begin{array}{rl}\sum _{i=1}^n{H}_i=\sum _{i=1}^n\sum _{j=1}^i\frac{1}{j}& =\sum _{i=1}^n\frac{1}{i}\cdot (n-i+1)\\ & =n\sum _{i=1}^n\frac{1}{i}-\sum _{i=1}^{n}1+\sum _{i=1}^n\frac{1}{i}\\ & =(n+1)H_n-n.\end{array}$

Zaburzanie

Gdy interesują nas skończone sumy odcinków początkowych ciągu ${\left\{a_i\right\}}_{i\in \mathbb{\mathbb{N}}}$, czyli sumy postaci $S_n=\sum _{i=0}^n{a}_i$. Metoda zaburzania polega na obliczeniu wartości $S_{n+1}$ za pomocą $S_n$ na dwa różne sposoby: na ogół wydzielając pierwszy i ostatni składnik sumy tzn.:

$S_n+a_{n+1}=a_0+\sum _{i=0}^n{a}_{i+1}$

Jeśli uda się nam ostatnią sumę wyrazić za pomocą $S_n$, to otrzymamy równanie, którego rozwiązanie jest poszukiwaną sumą. Niestety, metoda zaburzania dalece nie zawsze działa. Jednak w wielu sytuacjach bywa elegancka i skuteczna.

Przykład

Policzmy sumę $\sum _{i=0}^{n}a{x}^i$ skończonego ciągu geometrycznego dla $a,x\in \mathbb{\mathbb{Z}}$, $x\ne 1$. Zgodnie z ogólnym schematem zaburzania mamy:

$\begin{array}{rl}\sum _{i=0}^{n}a{x}^i+a{x}^{n+1}& =a{x}^0+\sum _{i=0}^{n}a{x}^{i+1}\\ & =a+x\sum _{i=0}^{n}a{x}^i\end{array}$

Rozwiązując powyższe równanie dostajemy:

$\sum _{i=0}^{n}a{x}^i=\frac{a-a{x}^{n+1}}{1-x}$ dla $x\ne 1$.

Przykład

Tym razem jesteśmy zainteresowani sumą $\sum _{i=0}^{n}i{2}^i$,która przyjmuje wartości:

$\begin{array}{ccccccc}n& 0& 1& 2& 3& 4& \dots \\ n{2}^n& 0& 2& 8& 24& 64& \dots \\ \sum _{i=0}^{n}i{2}^i& 0& 2& 10& 34& 98& \dots \end{array}$

Licząc przez zaburzanie dostajemy:

$\begin{array}{rl}\sum _{i=0}^{n}i{2}^i+(n+1)2^{n+1}& =0\cdot 2^0+\sum _{i=0}^n(i+1)2^{i+1}\\ & =2\sum _{i=0}^{n}i{2}^i+2\sum _{i=0}^n{2}^i\\ & =2\sum _{i=0}^{n}i{2}^i+2\cdot (2^{n+1}-1)\end{array}$

gdzie suma skończonego ciągu geometrycznego $\sum _{i=0}^n{2}^i$ została wyliczona w poprzednim przykładzie. Zatem ostatecznie

$\sum _{i=0}^{n}i{2}^i=(n+1)2^{n+1}-2(2^{n+1}-1)=(n-1)2^{n+1}+2$

Przykład

Spróbujmy policzyć jeszcze raz sumę kwadratów $\sum _{i=0}^n{i}^2$ ale tym razem przez zaburzanie.

$\begin{array}{rlrl}\sum _{i=0}^n{i}^2+(n+1{)}^2& =0^2+\sum _{i=0}^n(i+1{)}^2& =\sum _{i=0}^n{i}^2+2\sum _{i=0}^{n}i+\sum _{i=0}^{n}1& =\sum _{i=0}^n{i}^2+2\sum _{i=0}^{n}i+n\end{array}$

Niestety okazuje się, że sumy kwadratów się skracają. Zaburzanie okazało się w tym przypadku nieskuteczne. Zauważmy jednak, iż z otrzymanej równości $2\sum _{i=0}^{n}i=(n+1{)}^2-(n+1)$ dostajemy wzór na sumę kolejnych liczb naturalnych (a nie kwadratów jak chcieliśmy). Nasuwa się podejrzenie, że aby otrzymać wzór na sumę kwadratów trzeba zaburzyć sumę sześcianów. Spróbujmy:

$\begin{array}{rlrl}\sum _{i=0}^n{i}^3+(n+1{)}^3& =0^3+\sum _{i=0}^n(i+1{)}^3& =\sum _{i=0}^n{i}^3+3\sum _{i=0}^n{i}^2+3\sum _{i=0}^{n}i+\sum _{i=0}^{n}1& =\sum _{i=0}^n{i}^3+3\sum _{i=0}^n{i}^2+3\frac{n(n+1)}{2}+(n+1)\end{array}$

Rzeczywiście, sumy sześcianów się skracają i możemy wyprowadzić wzór na sumę kwadratów:

$\begin{array}{rlr}3\sum _{i=0}^n{i}^2& =(n+1{)}^3-\frac{3}{2}n(n+1)-(n+1)=(n+1)((n+1{)}^2-\frac{3}{2}n-1)\sum _{i=0}^n{i}^2& =\frac{(n+1)(n^2+2n+1-\frac{3}{2}n-1)}{3}=\frac{n(n+\frac{1}{2})(n+1)}{3}\end{array}$

Rachunek różnicowy

Żadna z przedstawionych metod obliczania skończonych sum nie jest niezawodnym kompletnym algorytmem. Są to raczej wskazówki bądź zestaw sztuczek, które czasem działają. Zaprezentujemy teraz podstawy rachunku różnicowego - dobrego narzędzia do obliczania skończonych sum.

Rachunek różnicowy powstał przez analogię do rachunku różniczkowego - działu matematyki zajmującego się badaniem funkcji rzeczywistych i zespolonych, przy użyciu ich pochodnych i całek. Podstawą rachunku różniczkowego jest operator pochodnej $D$, zdefiniowany jako

$(Df)(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

Przyporządkowuje on funkcję $Df$ funkcji rzeczywistej $f$. Odpowiednikiem operatora pochodnej w rachunku różnicowym jest operator różnicowy $\mathrm{\Delta }$, zdefiniowany jako

$(\mathrm{\Delta }f)(x)=f(x+1)-f(x)$

Przyporządkowuje on funkcję $\mathrm{\Delta }f$ funkcji rzeczywistej $f$. Będziemy go jednak rozważać tylko dla funkcji określonych na zbiorze liczb naturalnych (czyli dla ciągów). Operator $\mathrm{\Delta }$ to "skończony odpowiednik" operatora $D$. Rozważając funkcję liczb całkowitych $f$ nie mamy możliwości badać granicy występującej w definicji $D$. W zamian za to rozważamy stosowny iloraz $\frac{f(x+1)-f(x)}{1}$ przy najmniejszej możliwej wartości $h$.

MD1-3.2.swf

Przykład

Dla funkcji $f(x)=x^2-4x+10$ mamy

$\begin{array}{rl}(\mathrm{\Delta }f)(x)& =f(x+1)-f(x)=(x+1{)}^2-4(x+1)+10-(x^2-4x+10)\\ & =2x-3\end{array}$

$\begin{array}{cccccccc}n& 0& 1& 2& 3& 4& 5& \dots \\ f(n)& 10& 7& 6& 7& 10& 15& \dots \\ (\mathrm{\Delta }f)(n)& -3& -1& 1& 3& 5& \dots & \dots \end{array}$

Operator ${\mathrm{\Delta }}^n$ nazywamy n-tą iteracją operatora $\mathrm{\Delta }$, gdzie

$\begin{array}{rl}{\mathrm{\Delta }}^{0}f& =f,\\ {\mathrm{\Delta }}^{k+1}f& =\mathrm{\Delta }({\mathrm{\Delta }}^{k}f)\end{array}$

Przykład

Dla funkcji $f(x)=\sum _{i=0}^x{i}^2$ mamy:

• $(\mathrm{\Delta }f)(x)=f(x+1)-f(x)=\sum _{i=0}^{x+1}{i}^2-\sum _{i=0}^x{i}^2=(x+1{)}^2$,

• $({\mathrm{\Delta }}^{2}f)(x)=(\mathrm{\Delta }f)(x+1)-(\mathrm{\Delta }f)(x)=(x+1{)}^2-x^2=2x+1$,

• $({\mathrm{\Delta }}^{3}f)(x)=({\mathrm{\Delta }}^{2}f)(x+1)-({\mathrm{\Delta }}^{2}f)(x)=2(x+1)+1-(2x+1)=2$,

• $({\mathrm{\Delta }}^{4}f)(x)=({\mathrm{\Delta }}^{3}f)(x+1)-({\mathrm{\Delta }}^{3}f)(x)=2-2=0$.

$\begin{array}{cccccccc}x& 0& 1& 2& 3& 4& 5& \dots \\ HLINE\; TBDf(x)& 0& 1& 5& 14& 30& 55& \dots \\ (\mathrm{\Delta }f)(x)& 1& 4& 9& 16& 25& \dots \\ ({\mathrm{\Delta }}^{2}f)(x)& 3& 5& 7& 9& \dots \\ ({\mathrm{\Delta }}^{3}f)(x)& 2& 2& 2& \dots \\ ({\mathrm{\Delta }}^{4}f)(x)& 0& 0& \dots \end{array}$

Bardzo łatwo jest sprawdzić własności opisane w następnej obserwacji.

Obserwacja 4.1

Operator różnicowy $\mathrm{\Delta }$ jest operatorem liniowym, tzn.:

$\begin{array}{rl}\mathrm{\Delta }(c\cdot f)& =c\cdot \mathrm{\Delta }f,\\ \mathrm{\Delta }(f+g)& =\mathrm{\Delta }f+\mathrm{\Delta }g\end{array}$

Różniczkowanie jednomianów, czyli wielomianów typu $x^k$, jest bardzo proste: $D{x}^k=k{x}^{k-1}$ dla dowolnego $k⩾1$. Własność ta nie przenosi się jednak na operator $\mathrm{\Delta }$.

Przykład

$\begin{array}{rl}D{x}^2& =2x,\\ \mathrm{\Delta }{x}^2& =(x+1{)}^2-x^2=2x+1,\\ D{x}^3& =3x^2,\\ \mathrm{\Delta }{x}^3& =(x+1{)}^3-x^3=3x^2+3x+1\end{array}$

Na szczęście dla operatora różnicowego $\mathrm{\Delta }$ istnieją odpowiedniki jednomianów, czyli wielomianów o dowolnie dużych potęgach, które łatwo zróżnicować.

$m$-ta dolna silnia $x$ to wielomian zmiennej $x$, zdefiniowany jako

$x^{\underset{\_}{m}}=x(x-1)\dots (x-m+1)$, dla $m\ge 1$

$m$-ta górna silnia $x$ to wielomian zmiennej $x$, zdefiniowany jako

$x^{\bar{m}}=x(x+1)\dots (x+m-1)$, dla $m\ge 1$.

Dodatkowo przyjmujemy, że $x^{\underset{\_}{0}}=x^{\bar{0}}=1$.

Zauważmy, że w odróżnieniu od zwykłego potęgowania mamy tu

$x^{\underset{\_}{m+n}}=x^{\underset{\_}{m}}(x-m{)}^{\underset{\_}{n}}=(x-n{)}^{\underset{\_}{m}}{x}^{\underset{\_}{n}}$

Obserwacja 4.2

Dla $m\ge 1$ zachodzi $\mathrm{\Delta }{x}^{\underset{\_}{m}}=m{x}^{\underset{\_}{m-1}}$.

Dowód

$\begin{array}{rl}\mathrm{\Delta }{x}^{\underset{\_}{m}}& =(x+1{)}^{\underset{\_}{m}}-x^{\underset{\_}{m}}\\ & =(x+1)x(x-1)\dots (x-m+2)-x(x-1)\dots (x-m+1)\\ & =mx(x-1)\dots (x-m+2)\\ & =m{x}^{\underset{\_}{m-1}}\end{array}$

Twierdzenie 4.3

Dowolny wielomian $k$-tego stopnia $p(x)$ można jednoznacznie przedstawić w postaci $\sum _{i=0}^k{a}_i{x}^{\underset{\_}{k}}$, gdzie $a_0=p(0)$, $a_1=(\mathrm{\Delta }p)(0)$, $a_2=({\mathrm{\Delta }}^{2}p)(0)/2$ i ogólnie

$p(x)=\sum _{i=0}^k\frac{({\mathrm{\Delta }}^{i}p)(0)}{i!}{x}^{\underset{\_}{i}}$

Twierdzenie to jest analogią Twierdzenia Taylora dla wielomianów. Dowód pomijamy w tym wykładzie. Korzysta on z faktu, iż ciąg dolnych silni jest bazą przestrzeni liniowej wielomianów.

Wykorzystując Twierdzenie 4.3 możemy szybko różnicować dowolny wielomian $p(x)$ licząc jedynie kolejne różnice $({\mathrm{\Delta }}^{i}p)(0)$. To z kolei dla wielomianu stopnia $k$ sprowadza się do policzenia $k+2$ wartości początkowych $p(0),\dots ,p(k+1)$.

Przykład

Aby policzyć $\mathrm{\Delta }(x^3-5x+13)$ najpierw wyrażamy nasz wielomian jako kombinacje dolnych silni. Do tego potrzebujemy współczynników z Twierdzenia 4.3.

$\begin{array}{ccccccc}n& 0& 1& 2& 3& 4& \dots \\ HLINE\; TBD{n}^3-5n+13& 13& 9& 16& 25& 57& \dots \\ \mathrm{\Delta }(n^3-5n+13)& -4& 5& 9& 22& \dots \\ {\mathrm{\Delta }}^2(n^3-5n+13)& 9& 4& 11& \dots \\ {\mathrm{\Delta }}^3(n^3-5n+13)& -5& \dots \end{array}$

Potem różnicujemy wykorzystując podstawowe własności $\mathrm{\Delta }$.

$n^3-5n+13=\frac{-5}{6}{n}^{\underset{\_}{3}}+\frac{9}{2}{n}^{\underset{\_}{2}}+\frac{-4}{1}{n}^{\underset{\_}{1}}+\frac{13}{1}{n}^{\underset{\_}{0}}=-\frac{5}{6}{n}^{\underset{\_}{3}}+\frac{9}{2}{n}^{\underset{\_}{2}}-4n^{\underset{\_}{1}}+13$,

by dostać

$\begin{array}{rl}\mathrm{\Delta }(n^3-5n+13)& =\mathrm{\Delta }(-\frac{5}{6}{n}^{\underset{\_}{3}}+\frac{9}{2}{n}^{\underset{\_}{2}}-4n^{\underset{\_}{1}}+13)\\ & =-\frac{5}{6}\cdot 3n^{\underset{\_}{2}}+\frac{9}{2}\cdot 2n^{\underset{\_}{1}}-4\cdot 1\\ & =-\frac{5}{2}{n}^{\underset{\_}{2}}+9n^{\underset{\_}{1}}-4.\end{array}$

W rachunku różniczkowym operator pochodnej $D$ ma operator odwrotny - jest nim operator całki $\int$. Te dwa operatory powiązane są własnością:

$g=Df$ wtedy i tylko wtedy, gdy $\int g(x)dx=f(x)+C$

Zauważmy, że wychodząc od funkcji $g:\mathbb{\mathbb{N}}⟶\mathbb{ℝ}$ i definiując $f:\mathbb{\mathbb{N}}⟶\mathbb{ℝ}$ poprzez $f(n)=\sum _{i=0}^{n-1}g(i)$ mamy $\mathrm{\Delta }f=g$. Moglibyśmy więc zdefiniować sumę nieoznaczoną jako $\sum g(x)\delta x=\sum _{i=0}^{n-1}g(i)$. Ponieważ $\mathrm{\Delta }f=\mathrm{\Delta }(f+C)$ dla dowolnej stałej $C$, to - podobnie jak w przypadku całki nieoznaczonej - suma nieoznaczona zdefiniowana jest tylko z dokładnością do stałej addytywnej:

$g=\mathrm{\Delta }f$ wtedy i tylko wtedy, gdy $\sum g(x)\delta x=f(x)+C$

Tak więc $\sum g(x)\delta x$ (podobnie jak $\int g(x)dx$) jest klasą funkcji, których różnica (pochodna) równa jest $g(x)$. Wyrażenie $\sum g(x)\delta x$ to suma nieoznaczona funkcji $g(x)$. Następujące własności sumy nieoznaczonej wynikają wprost z własności $\mathrm{\Delta }$:

Obserwacja 4.4

Dla funkcji $f,g:\mathbb{\mathbb{N}}⟶\mathbb{ℝ}$ oraz $c\in \mathbb{ℝ}$ zachodzi:

• $\sum c\cdot g(x)\delta x=c\cdot \sum g(x)\delta x$,

• $\sum (f(x)+g(x))\delta x=\sum f(x)\delta x+\sum g(x)\delta x$,

• $\sum x^{\underset{\_}{m}}\delta x=\frac{1}{m+1}{x}^{\underset{\_}{m+1}}$, dla $m⩾0$.

Suma oznaczona funkcji $g(x)$ o parametrach $a,b\in \mathbb{\mathbb{N}}$ to

$\sum _a^{b}g(x)\delta x=f(b)-f(a)$,

dla funkcji $f$ z klasy $\sum g(x)\delta x$, tzn. takiej, że $g=\mathrm{\Delta }f$, czyli $g(x)=f(x+1)-f(x)$. Zauważmy, ze definicja ta jest poprawna, tzn. nie zależy od wyboru funkcji $f$, jako stała, o którą dwie takie funkcje się różnią zniesie się przy przy odejmowaniu. Nie będzie to bardzo zaskakujące po udowodnieniu poniższych własności sumy oznaczonej, które są analogiami własności całki oznaczonej.

Obserwacja 4.5

Dla dowolnych całkowitych $a,b,c$ zachodzi:

• $\sum _a^{a}g(x)\delta x=0$,

• $\sum _a^{a+1}g(x)\delta x=g(a)$,

• $\sum _a^{b}g(x)\delta x=-\sum _b^{a}g(x)\delta x$,

• $\sum _a^{b}g(x)\delta x+\sum _b^{c}g(x)\delta x=\sum _a^{c}g(x)\delta x$,

• $\sum _a^{b}g(x)\delta x=\sum _{a\le i<b}g(i)$, o ile tylko $a\le b$.

Dowód

Pierwsze cztery własności wynikają natychmiast z definicji sumy oznaczonej. Dowód piątej poprowadzimy indukcyjnie z uwagi na $b\ge a$. Dla $b=a$ jest to pierwszy punkt naszej obserwacji. Nadto $\sum _a^{b+1}g(x)\delta x=\sum _a^{b}g(x)\delta x+\sum _b^{b+1}g(x)\delta =\sum _{a\le i<b}g(i)+g(b)=\sum _{a\le i<b+1}g(i)$, gdzie pierwsza równość jest konsekwencją punktu czwartego, a druga punktu drugiego.

Rachunek różnicowy w liczeniu sum skończonych

Wracamy teraz do rozważań o sumach skończonych. Zobaczymy, jak rachunek różnicowy może być pomocny w ich obliczaniu. Widzieliśmy już, że suma $\sum _{a\le i<b}g(i)$to dokładnie $f(b)-f(a)$, gdzie $f$ jest sumą nieoznaczoną funkcji $g$, tzn. $g(x)=f(x+1)-f(x)$. Wystarczy więc wyliczyć sumę nieoznaczoną. A proces ten jest bardzo podobny jak liczenie całek nieoznaczonych. W kolejnych przykładach zobaczymy, jak to można zrobić w praktyce.

Przykład

Dla policzenia sumy dolnych silni $\sum _{i=0}^n{i}^{\underset{\_}{2}}$ odnotujmy najpierw, że skoro $\mathrm{\Delta }{x}^{\underset{\_}{3}}=3x^{\underset{\_}{2}}$, to $\sum x^{\underset{\_}{2}}\delta x=\frac{x^{\underset{\_}{3}}}{3}+C$. Teraz już oczywiście $\sum _{i=0}^n{i}^{\underset{\_}{2}}=\sum _0^{n+1}{x}^{\underset{\_}{2}}\delta x=\frac{(n+1{)}^{\underset{\_}{3}}}{3}-\frac{0^{\underset{\_}{3}}}{3}=\frac{(n+1{)}^{\underset{\_}{3}}}{3}$.
Podobnie przy liczeniu $\sum _{i=0}^n{i}^{\underset{\_}{k}}$, gdzie $k\ge 0$, wykorzystujemy fakt, iż $\mathrm{\Delta }{x}^{\underset{\_}{k+1}}=(k+1)x^{\underset{\_}{k}}$ i dostajemy $\sum _{i=0}^n{i}^{\underset{\_}{k}}=\sum _0^{n+1}{x}^{\underset{\_}{k}}\delta x=\frac{(n+1{)}^{\underset{\_}{k+1}}}{k+1}$.

Przykład

Dla policzenia sumy sześcianów $\sum _{i=0}^n{i}^3$ potrzebujemy najpierw znaleźć sumę nieoznaczoną $\sum x^3\delta x$. W tym celu wykorzystujemy najpierw Twierdzenie 4.3 do przedstawienia wielomianu $x^3$ jako kombinacji liniowej dolnych silni, dla których znamy już sumy nieoznaczone. Liczymy więc współczynniki typu $\frac{({\mathrm{\Delta }}^i{x}^3)(0)}{i!}$:

$\begin{array}{ccccccc}x& 0& 1& 2& 3& 4& \dots \\ HLINE\; TBD{x}^3& 0& 1& 8& 27& 64& \dots \\ \mathrm{\Delta }{x}^3& 1& 7& 19& 37& \dots \\ {\mathrm{\Delta }}^2{x}^3& 6& 12& 18& \dots \\ {\mathrm{\Delta }}^3{x}^3& 6& 6& \dots \end{array}$

skąd

$x^3=\frac{6}{3!}{x}^{\underset{\_}{3}}+\frac{6}{2!}{x}^{\underset{\_}{2}}+\frac{1}{1!}{x}^{\underset{\_}{1}}+0=x^{\underset{\_}{3}}+3x^{\underset{\_}{2}}+x^{\underset{\_}{1}}$,

a zatem

$\sum x^3=\sum (x^{\underset{\_}{3}}+3x^{\underset{\_}{2}}+x^{\underset{\_}{1}})\delta x=\frac{x^{\underset{\_}{4}}}{4}+x^{\underset{\_}{3}}+\frac{x^{\underset{\_}{2}}}{2}+C$,

i wreszcie

$\sum _{i=0}^n{i}^3=\sum _0^{n+1}{x}^3\delta x=\sum _0^{n+1}(x^{\underset{\_}{3}}+3x^{\underset{\_}{2}}+x^{\underset{\_}{1}})\delta x=\frac{(n+1{)}^{\underset{\_}{4}}}{4}+(n+1{)}^{\underset{\_}{3}}+\frac{(n+1{)}^{\underset{\_}{2}}}{2}$

Uwalniając się teraz od dolnych silni dostajemy, że to ostatnie wyrażenie wynosi

$\frac{(n+1)n(n-1)(n-2)+4(n+1)n(n-1)+2(n+1)n}{4}=\frac{(n+1{)}^2{n}^2}{4}$

Rozszerzymy teraz pojęcie dolnej silni na ujemne wykładniki kładąc :

$x^{\underset{\_}{-m}}=\frac{1}{(x+1)(x+2)\dots (x+m)}$, dla $m>0$

Prawa dla dolnej silni, które odnotowaliśmy dla wykładników naturalnych są zachowane. W szczególności mamy:

Obserwacja 4.6

Dla dowolnych $m,n\in \mathbb{\mathbb{Z}}$ zachodzi:

• $x^{\underset{\_}{m+n}}=x^{\underset{\_}{m}}(x-m{)}^{\underset{\_}{n}}$,

• $\mathrm{\Delta }{x}^{\underset{\_}{m}}=m\cdot x^{\underset{\_}{m-1}}$,

• $\sum x^{\underset{\_}{m}}\delta x=\frac{x^{m+1}}{m+1}+C$, dla $m\ne -1$.

Dowód tej obserwacji zostawiamy jako ćwiczenie. Zajmiemy się natomiast jedynym przypadkiem, którego nie potrafimy jeszcze sumować, tzn. wyrażeniem $\sum x^{\underset{\_}{-1}}\delta x$. Oczywiście $x^{\underset{\_}{-1}}$ to $\frac{1}{x+1}$. Widzieliśmy również, że suma postaci $\sum _{i=0}^n\frac{1}{i+1}$ to $(n+1)$-sza liczba harmoniczna $H_{n+1}$ oraz zachowuję się podobnie do logarytmu:

$\frac{\lfloor \lg n\rfloor +1}{2}\le H_n\le \lfloor \lg n\rfloor +1$

Z rachunku całkowego wiemy natomiast, że $\int x^{-1}dx=\ln x+C$. Następna obserwacja pokazuje, że podobieństwo to nie jest przypadkowe:

Obserwacja 4.7

$\mathrm{\Delta }{H}_x=x^{\underset{\_}{-1}}$ oraz $\sum x^{\underset{\_}{-1}}\delta x=H_x+C$.

Dowód

Mamy

$\mathrm{\Delta }{H}_x=\mathrm{\Delta }(1+\frac{1}{2}+\dots +\frac{1}{x})=(1+\dots +\frac{1}{x}+\frac{1}{x+1})-(1+\dots +\frac{1}{x})=\frac{1}{x+1}=x^{\underset{\_}{-1}}$,

skąd natychmiast $\sum x^{\underset{\_}{-1}}\delta x=H_x+C$.

Z kolei dyskretnym odpowiednikiem funkcji wykładniczej $e^x$, która nie zmienia się przy różniczkowaniu, jest funkcja $2^x$:

Obserwacja 4.8

Dla liczby rzeczywistej $c\ne 1$ mamy $\mathrm{\Delta }{c}^x=(c-1)c^x$ oraz $\sum c^x\delta x=\frac{c^x}{c-1}+C$. W szczególności $\mathrm{\Delta }{2}^x=2^x$ oraz $\sum 2^x\delta x=2^x+C$.

Dowód

Istotnie, $\mathrm{\Delta }{c}^x=c^{x+1}-c^x=(c-1)c^x$, skąd (jeśli tylko $c\ne 1$) dostajemy natychmiast $\sum c^x\delta x=\frac{c^x}{c-1}+C$.

Przykład

Używając rachunku różnicowego policzymy teraz sumę skończonego ciągu geometrycznego $\sum _{i=0}^{n}ab{q}^i$ z ilorazem $q\ne 1$. Obserwacje 4.4 i 4.8 dają:

$\sum a{q}^x\delta x=a\sum q^x\delta x=a\frac{q^x}{q-1}+C$

A zatem:

$\sum _{i=0}^{n}a{q}^i=a\frac{q^n}{q-1}-a\frac{q^0}{q-1}=a\frac{q^n-1}{q-1}$

Sumowanie przez części

Poprzez analogię do rachunku różnicowego zastosujmy operator różnicowy do iloczynu funkcji

$\begin{array}{rl}\mathrm{\Delta }(f(x)g(x))& =f(x+1)g(x+1)-f(x)g(x)\\ & =f(x+1)g(x+1)-f(x)g(x+1)+f(x)g(x+1)-f(x)g(x)\\ & =g(x+1)\mathrm{\Delta }f+f(x)\mathrm{\Delta }g(x).\end{array}$

Dostajemy stąd natychmiast następującą regułę sumowania przez części

Obserwacja 4.9

$\sum f(x)\cdot \mathrm{\Delta }g(x)\delta x=f(x)\cdot g(x)-\sum (\mathrm{\Delta }f)(x)\cdot g(x+1)\delta x$.

Przykład

Dla policzenia sumy $\sum _{i=0}^{n}i{2}^i$, wyznaczamy najpierw (przez części) sumę nieoznaczoną $\sum (x{2}^x)\delta x$. Jest to łatwe, jako że $2^x=\mathrm{\Delta }{2}^x$, więc

$\begin{array}{rl}\sum (x{2}^x)\delta x& =x{2}^x-\sum ((\mathrm{\Delta }x)2^{x+1})\delta x\\ & =x{2}^x-\sum (1\cdot 2^{x+1})\delta x\\ & =x{2}^x-2^{x+1}+C=(x-2)2^x+C.\end{array}$

Teraz mamy już

$\sum _{i=0}^{n}i{2}^i=\sum _0^{n+1}x{2}^x\delta x=(n+1-2)2^{n+1}-(0-2)2^0=(n-1)2^{n+1}-2$