TC Moduł 5

Redukcja argumentów

Minimalizacja funkcji boolowskich jest podstawową procedurą syntezy logicznej w komputerowych systemach projektowania układów cyfrowych. Skuteczność i szybkość działania tej procedury może być decydująca o jakości implementacji sprzętowych wielu systemów cyfrowych o różnorodnych zastosowaniach.

Niestety ze względu na heurystyczny sposób obliczeń w programie Espresso uzyskany wynik $F_{M}$ może nie być pokryciem minimalnym, co przy wzrastającej złożoności układów realizowanych w nowoczesnych technologiach może okazać się istotną barierą.

Niniejszy wykład omawia oryginalną metodę zmniejszania złożoności obliczeniowej algorytmów minimalizacji funkcji boolowskich. Istotą tej metody jest zastosowanie algorytmu redukcji argumentów, jako oddzielnej procedury poprzedzającej właściwą minimalizację. Redukcja argumentów jest procedurą do tej pory rzadko stosowaną w komputerowych systemach syntezy logicznej. Jedną z przyczyn takiej sytuacji jest brak świadomości, że złożone układy cyfrowe są – od strony pojedynczych wyjść - reprezentowane funkcjami boolowskimi o znacznie nadmiarowych zależnościach wejściowych.

Celem wprowadzenia wróćmy do przykładu funkcji omawianej w poprzednim wykładzie. Jej tablica prawdy podana na planszy ma 7 argumentów. Ale na poprzednim wykładzie obliczyliśmy metodą ekspansji, że minimalne wyrażenie boolowskie tej funkcji zawiera wyłącznie 4 argumenty. Gdybyśmy to wiedzieli wcześniej, to zadanie minimalizacji moglibyśmy skutecznie uprościć. Wystarczyłoby w tym celu usunąć z tablicy prawdy tej funkcji kolumny odpowiadające nadmiarowym argumentom. Zatem problem obliczania od jakich argumentów funkcja istotnie zależy jest bardzo ważny w zmniejszaniu złożoności obliczeniowej procedur minimalizacji.

W innym przykładzie funkcji 10 argumentowej, dla której programem Espresso zostało obliczone minimalne wyrażenie boolowskie zauważamy, że w wyrażeniu tym brak jest zmiennej

x_{3}

. Czyli według Espresso funkcja ta zależy od 9 argumentów.

Można jednak obliczyć (programem Pandor), że funkcja ta w rzeczywistości jest zależna od 7 argumentów. Czyli Espresso doskonale redukuje składniki iloczynowe funkcji, ale w przypadku argumentów jego obliczenia nie są skuteczne. Potwierdza to sygnalizowany już mankament metody i programu Espresso.

Z powyższych przykładów wynika, że obliczanie minimalnej liczby argumentów

od których funkcja istotnie zależy jest bardzo istotne w redukowaniu złożoności obliczeniowej procedur minimalizacji funkcji boolowskich, a w konsekwencji może się przyczynić do uzyskiwania lepszych rezultatów. Do obliczeń w metodzie redukcji argumentów będziemy stosować rachunek podziałów. Niezbędne pojęcia tego rachunku podajemy na planszach 7, 8 oraz 9.

Podziałem na zbiorze

S

jest system zbiorów

π = {B i}

, którego bloki są rozłączne, czyli

B_{i} \cap B_{j} = \emptyset

, jeśli tylko

i \neq j

.

Na przykład dla $S = {1, 2, 3, 4, 5, 6}$ , ${{1, 2}, {3, 5}, {4, 6}}$ jest podziałem na $S$ , co zapisujemy:

π = (\overline{1, 2}; \overline{3, 4}; \overline{5, 6})

Dla podziałów – podobnie jak dla zbiorów –definiuje się relację porządku oraz typowe działania iloczynu, sumy itp.,

Powiemy, że podział

π_{1}

jest nie większy od

π_{2}

(co oznaczamy:

π_{1} \leq π_{2}

), jeśli każdy blok z

π_{1}

jest zawarty w pewnym bloku z

π_{2}

.

Wprowadzamy oznaczenia odpowiednio dla podziału najmniejszego $π (0)$ oraz największego $π (1)$ . Podział $π (0)$ jest podziałem, którego bloki są elementami zbioru $S$ . Podział $π (1)$ jest podziałem o jednym bloku wyczerpującym cały zbiór $S$ . Na przykład: dla Parser nie mógł rozpoznać (błąd składni): {\displaystyle S = \left\{1, 2, 3}\right\}\,} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle \pi (0) = \left\{\overline{1}, \overline{2}, \overline{3}}\right\}\,} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle \pi (1) = \left\{\overline{1,2,3}}\right\}\,} .

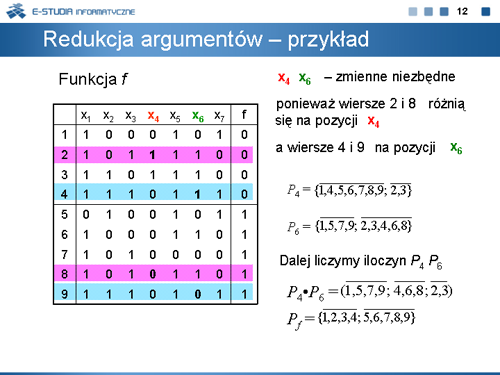
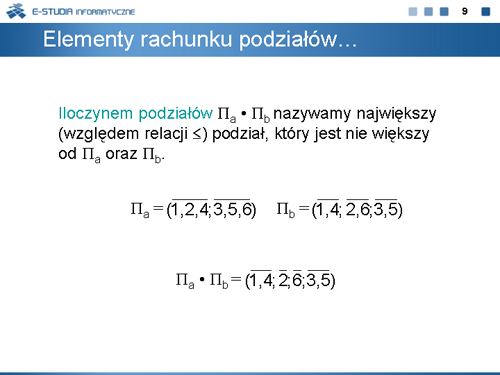
Iloczynem podziałów

π_{1} ∙ π_{2}

nazywamy największy (względem relacji

\leq

) podział, który jest nie większy od

π_{1}

oraz

π_{2}

.

$Π_{a} = (\overline{1, 2, 4}; \overline{3, 5, 6})$

$Π_{b} = (\overline{1, 4}; \overline{2, 6}; \overline{3, 5})$

$Π_{1} ∙ Π_{2} = (\overline{1, 4}; \overline{2}; \overline{6}; \overline{3, 5})$

Symetrycznie, sumą $π_{1} + π_{2}$ nazywamy najmniejszy podział nie mniejszy od $π_{1}$ oraz $π_{2}$ .

$Π_{a} = (\overline{1, 2}; \overline{3, 4}; \overline{5, 6}; \overline{7, 8, 9})$

$Π_{b} = (\overline{1, 6}; \overline{2, 3}; \overline{4, 5}; \overline{7, 8}; \overline{9})$

$Π_{1} + Π_{2} = (\overline{1, 2, 3, 4, 5, 6}; \overline{7, 8, 9})$

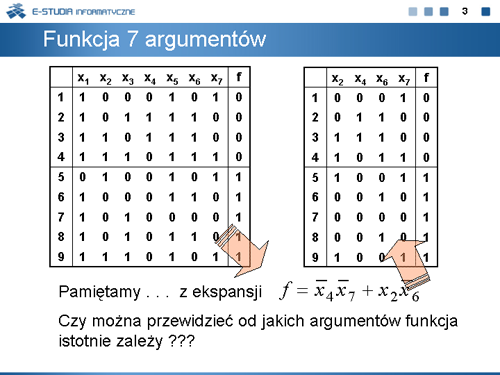
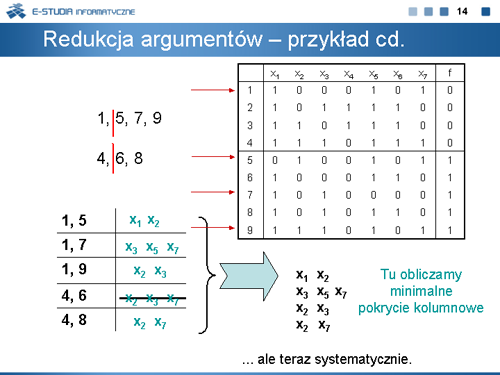
Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący:

$P_{1} = (\overline{5}; \overline{1, 2, 3, 4, 6, 7, 8, 9})$

$P_{2} = (\overline{1, 2, 6, 7, 8}; \overline{3, 4, 5, 9})$

$P_{3} = (\overline{1, 3, 5, 6}; \overline{2, 4, 7, 8, 9})$

$P_{4} = (\overline{1, 4, 5, 6, 7, 8, 9}; \overline{2, 3})$

$P_{5} = (\overline{7}; \overline{1, 2, 3, 4, 5, 6, 8, 9})$

$P_{6} = (\overline{1, 5, 7, 9}; \overline{2, 3, 4, 6, 8})$

$P_{7} = (\overline{2, 3, 6, 7, 8}; \overline{1, 4, 5, 9})$

$P_{f} = (\overline{1, 2, 3, 4}; \overline{5, 6, 7, 8, 9})$

Jeżeli wektory

X_{a}

oraz

X_{b}

:

f (X_{a}) \neq f (X_{b})

, różnią się dokładnie dla jednej zmiennej to nazywamy ją zmienną niezbędną. Sens fizyczny zmiennej niezbędnej wynika z faktu, że usunięcie kolumny odpowiadającej tej zmiennej w tablicy prawdy tworzy tablicę, w której dwa takie same wektory mają różne wartości (są sprzeczne).

Na przykładzie funkcji EXTL wyjaśniamy poszukiwanie zmiennych niezbędnych.

Zmiennymi niezbędnymi tej funkcji są $x_{4}$ , $x_{6}$ . Co łatwo sprawdzić, gdyż wiersze o numerach 2 i 8 (zaznaczone kolorem różowym) różnią się wyłącznie na pozycji $x_{4}$ , natomiast wiersze 4 i 9 (zaznaczone kolorem niebieskim) różnią się tylko na pozycji $x_{6}$ .

Po wyznaczeniu zmiennych niezbędnych obliczamy iloczyn podziałów $P = P_{4} \cdot P_{6}$ .

Iloczyn podziałów wyznaczonych przez zmienne niezbędne ma bardzo ważną interpretację.

Zauważmy, że kolejne bloki iloczynu $P = (B_{1}, \dots, B_{3})$ są $B_{1} = {1, 5, 7, 9}$ , $B_{2} = {4, 6, 8}$ , Parser nie mógł rozpoznać (błąd składni): {\displaystyle B_3 = {2,3\}} .Blok $B_{3}$ jest zawarty w jednym bloku podziału $P_{f}$ . Ale bloki $B_{1}$ i $B_{2}$ zawierają elementy należące do dwóch różnych bloków podziału $P_{f}$ , czyli same zmienne $x_{4}$ , $x_{6}$ nie wystarczają do oddzielenia wektorów prawdziwych od fałszywych realizowanej funkcji.

Zatem należy się zastanowić jakie argumenty należy dołożyć do argumentów niezbędnych, aby zapewnić jednoznaczną realizację tej funkcji. Obserwując zbiory

B_{1} = {1, 5, 7, 9}

,

B_{2} = {4, 6, 8}

, łatwo stwierdzić, że wystarczy w tym celu dobrać takie argumenty, aby „oddzielić” wektory (wiersze) o numerach 1 od 5, 7, 9 oraz 4 od 6, 8. Zatem należy oddzielić 1 od 5, 1 od 7 itd. Zapisujemy zbiory argumentów, dla których różnią się wiersze 1 i 5, 1 i 7 itd. w formie stosownej tabelki (jak na planszy). W tabelce tej zbiór w wierszu oznaczonym 4, 6 pokrywa zbiór z wiersza 1, 9. Zatem wiersz „większy” usuwamy.

Ogólnie usuwamy każdy zbiór $Z$ dla którego istnieje $Z^{'} : Z^{'} \subseteq Z$ . Tak wyznaczana tabelka (w szczególności) zredukowana może być interpretowana jako zadanie obliczania minimalnego pokrycia kolumnowego.

Chcąc zatem obliczyć minimalne zbiory argumentów zapisujemy zredukowaną tabelkę w postaci wyrażenia boolowskiego typu „iloczyn sum”. Kolejną czynnością jest przekształcenie „iloczynu sum” w wyrażenie typu „suma iloczynów” W czynności tej oczywiście stosujemy zasady algebry Boole’a. I w rezultacie uzyskujemy wyrażenie:

$x_{2} x_{3} + x_{2} x_{5} + x_{2} x_{7} + x_{1} x_{3} x_{7} +$

które interpretujemy następująco. Wszystkie składniki tego wyrażenia o minimalnej liczbie czynników (zmiennych $x_{i}$ ) reprezentują minimalne zbiory argumentów, które łącznie ze zmiennymi niezbędnymi tworzą minimalne zbiory argumentów wystarczające do realizacji funkcji:

${x_{2}, x_{3}, x_{4}, x_{6}}, {x_{2}, x_{3}, x_{5}, x_{6}}, {x_{2}, x_{3}, x_{6}, x_{7}}$ .

Stąd wniosek, że siedmio-argumentowa funkcja f w rzeczywistości jest zależna wyłącznie od czterech argumentów.

Zauważmy też, że ostatnie z podanych rozwiązań oznacza usunięcie z tablicy funkcji

f

kolumn odpowiadających zmiennym

x 1, x 3, x 5

. W rezultacie uzyskujemy tablicę, której wymiary umożliwiają zastosowanie nawet najprostszej metody minimalizacji jaką jest tablica Karnaugha.

Omówioną metodę zrealizowaną w postaci oddzielnego modułu oprogramowania można traktować jako procedurę wspomagająca metodę i program Espresso. W celu przekonania się o skuteczności wspomagania minimalizacji funkcji boolowskich dodatkową procedurą redukcji argumentów omówimy kilka eksperymentów wykonanych programami Espresso i Pandor. W eksperymentach tych dokonamy minimalizacji dwóch typowych funkcji boolowskich: TL27 i KAZ. W szczególności porównamy wyniki minimalizacji uzyskane programem Espresso z wynikami uzyskanymi przy wspomaganiu minimalizacji dodatkową procedura redukcji argumentów.

Eksperyment z funkcją TL27. Na planszy z lewej strony podany jest plik wejściowy programu Espresso z zapisaną funkcją TL27. Z prawej strony tej planszy podany jest wynik minimalizacji tej funkcji programem Espresso. Jak widać espresso minimalizuje tę funkcję do 6 termów (składników iloczynowych) z łączną liczbą 9 argumentów.

Za pomocą programu Pandor można obliczyć, że funkcja ta ma 10 rozwiązań dla minimalnych zbiorów argumentów. Jedno z tych rozwiązań jest podane na planszy. Jest zrozumiałe, że funkcja o mniejszej liczbie argumentów jest „łatwiejsza” do minimalizacji. Zatem tak zredukowaną funkcję można poddać obliczeniom za pomocą programu Pandor.

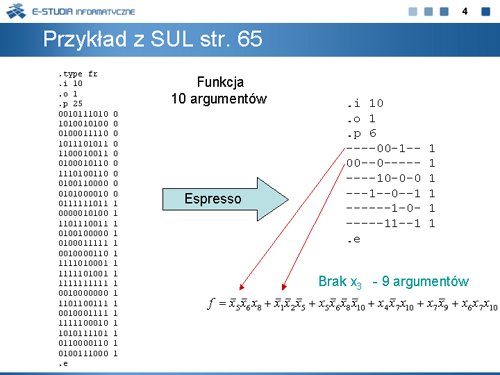
Porównajmy wyniki tak przeprowadzanych minimalizacji.

Wynik Espresso – 9 argumentów, 6 termów

$f = {\overline{x}}_{5} {\overline{x}}_{6} x_{8} + {\overline{x}}_{1} {\overline{x}}_{2} {\overline{x}}_{5} + x_{5} {\overline{x}}_{6} {\overline{x}}_{8} {\overline{x}}_{10} + x_{4} {\overline{x}}_{7} x_{10} + x_{7} {\overline{x}}_{9} + x_{6} x_{7} x_{10}$

Wynik Pandora – 7 argumentów, 5 termów

$f = {\overline{x}}_{1} {\overline{x}}_{2} {\overline{x}}_{7} + x_{1} x_{2} x_{4} + {\overline{x}}_{1} x_{10} + {\overline{x}}_{1} {\overline{x}}_{4} {\overline{x}}_{6} + x_{7} {\overline{x}}_{9}$

Eksperyment z funkcją KAZ. Na planszy z lewej strony podany jest plik wejściowy programu Espresso z zapisaną funkcją KAZ. Z prawej strony tej planszy podany jest wynik redukcji argumentów tej funkcji programem Pandor. Jak widać Pandor oblicza, że funkcja ta w rzeczywistości (mimo pierwotnej specyfikacji o 21 argumentach) istotnie zależy wyłącznie od 5 argumentów. Zatem tak zredukowaną funkcję można poddać obliczeniom za pomocą systematycznej procedury ekspansji wbudowanej do programu Pandor.

Możemy więc porównać wynik minimalizacji programem Espresso:

$f = {\overline{x}}_{2} x_{14} {\overline{x}}_{19} x_{21} + x_{7} {\overline{x}}_{8} {\overline{x}}_{12} + x_{5} x_{8} {\overline{x}}_{20}$

z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów.

$f = {\overline{x}}_{2} {\overline{x}}_{4} x_{9} {\overline{x}}_{19} + {\overline{x}}_{2} x_{4} {\overline{x}}_{9} + x_{2} x_{19} {\overline{x}}_{20}$

</math>

TC Moduł 5

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia