Matematyka dyskretna 2/Ćwiczenia 1: Zagadnienia Mini-Maksowe w grafach

Zagadnienia Mini-Maksowe w grafach

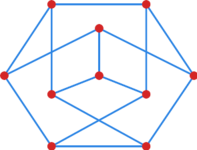
Ćwiczenie 1

Czy graf Petersena przedstawiony na rysunku 1 ma skojarzenie doskonałe? Odpowiedź uzasadnij.

Rozwiązanie

Ćwiczenie 2

Kostka $k$ -wymiarowa $𝒬_{k}$ to graf, którego wierzchołki są ciągami $(a_{1}, a_{2}, \dots, a_{k})$ , gdzie $a_{i} = 0, 1$ , a krawędzie łączą te ciągi, które różnią się na jednej tylko pozycji. W kostce $𝒬_{k}$ znajdź

maksymalne skojarzenie,
minimalne pokrycie krawędziowe,
minimalne pokrycie wierzchołkowe,
maksymalny zbiór niezależny,

i podaj ich liczności.

Wskazówka

Kostka $𝒬_{k}$ ma skojarzenie doskonałe. Będzie ono więc też minimalnym pokryciem krawędziowym. Ponieważ kostka $𝒬_{k}$ jest grafem dwudzielnym, w poszukiwaniu minimalnego pokrycia wierzchołkowego można użyć Twierdzenie Koniga 1.4.

Rozwiązanie

Maksymalne skojarzenie: $ν (𝒬_{k}) = 2^{k - 1}$ .

Skojarzenie $M$ ciągu $(0, a_{2}, \dots, a_{k})$ z ciągiem $(1, a_{2}, \dots, a_{k})$ jest doskonałe i zawiera $| V (𝒬_{k}) | / 2 = 2^{k - 1}$ krawędzi.

Minimalne pokrycie krawędziowe: $ρ (𝒬_{k}) = 2^{k - 1}$ .

Zdefiniowane wyżej skojarzenie maksymalne $M$ jest doskonałe, więc $M$ jest pokryciem krawędziowym. Na mocy Twierdzenia 1.2 wiemy, że maksymalne skojarzenie zawiera się w jakimś minimalnym pokryciu krawędziowym. Pokrycie krawędziowe $M$ jest więc minimalne.

Minimalne pokrycie wierzchołkowe: $τ (𝒬_{k}) = 2^{k - 1}$ .

Kostka $𝒬_{k}$ jest grafem dwudzielnym, więc korzystając z Twierdzenia Koniga 1.4 otrzymujemy, że minimalne pokrycie wierzchołkowe ma

τ (𝒬_{k}) = ν (𝒬_{k}) = 2^{k - 1}

elementów. Pozostaje jedynie wskazać takie pokrycie wierzchołkowe o $2^{k - 1}$ elementach. Pokażemy, że zbiór $C$ wszystkich ciągów o nieparzystej liczbie jedynek jest takim pokryciem. Każda krawędź $e \in E (𝒬_{k})$ łączy ciągi o różnej parzystości jedynek, więc $e$ jest incydentna z jakimś wierzchołkiem z $C$ . Zbiór $C$ jest więc pokryciem wierzchołkowym. Ciągów o parzystej liczbie jedynek jest dokładnie tyle, co o nieparzystej liczbie jedynek. A zatem $| C | = 2^{k} / 2 = 2^{k - 1}$ , czyli pokrycie wierzchołkowe $C$ jest minimalne.

Maksymalny zbiór niezależny: $α (𝒬_{k}) = 2^{k - 1}$ .

Z Twierdzenia Gallai 1.1 wiemy, że

α (𝐆) = | V (𝐆) | - τ (𝐆) = 2^{k} - 2^{k - 1} = 2^{k - 1}

Wystarczy więc znaleźć zbiór niezależny o $2^{k - 1}$ elementach. Zbiór $C$ jest oczywiście niezależny, bo każda krawędź w kostce łączy ciągi różniące się parzystością jedynek. Z drugiej strony, zbiór $C$ realizuje wartość $α (𝐆) = 2^{k - 1}$ , więc jest maksymalnym zbiorem niezależnym.

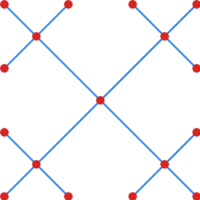
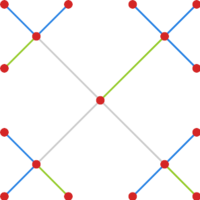
Ćwiczenie 3

Wskaż minimalne pokrycie krawędziowe $C$ drzewa $𝐓_{1}$ z rysunku 3 oraz maksymalne skojarzenie $M$ zawarte w tym pokryciu.

Wskazówka

Rozwiązanie

Na rysunku 4 kolorami niebieskim i zielonym zostały zaznaczone krawędzie z minimalnego pokrycia, przy czym zielone krawędzie tworzą maksymalne skojarzenie.

Ćwiczenie 4

Pokaż, że w grafie prostym $𝐆$ bez punktów izolowanych, maksymalne, w sensie inkluzji, skojarzenie $M$ jest najbardziej liczne wtedy i tylko wtedy, gdy $M$ jest zawarte w jakimś minimalnym pokryciu krawędziowym $𝐆$ .

Wskazówka

Rozwiązanie

Niech $M$ będzie najliczniejszym skojarzeniem w grafie $𝐆$ , czyli $| M | = ν (𝐆)$ . Wtedy $I = V (𝐆) - V (M)$ jest zbiorem niezależnym i ma $| V (𝐆) | - 2 \cdot ν (𝐆)$ elementów. Ponieważ $𝐆$ nie ma punktów izolowanych, to każdy wierzchołek z $I$ jest połączony krawędzią z jakimś wierzchołkiem ze zbioru $V (M)$ . Dla każdego wierzchołka $v \in I$ wybierzmy krawędź incydentną z $v$ . Zbiór tak wybranych krawędzi w sumie z $M$ tworzy pokrycie krawędziowe $C_{e}$ grafu $𝐆$ . W $C_{e}$ jest $ν (𝐆)$ krawędzi ze skojarzenia $M$ oraz $| V (𝐆) | - 2 \cdot ν (𝐆)$ krawędzi incydentnych z elementami $I$ . A zatem $C_{e}$ ma

| {C_{e}}^{'} | = ν (𝐆) + (| V (𝐆) | - 2 \cdot ν (𝐆)) = | V (𝐆) | - ν (𝐆) = ρ (𝐆)

elementów.

Dla dowodu implikacji odwrotnej niech skojarzenie $M$ zawiera się w minimalnym pokryciu krawędziowym $C$ . Pokrycie krawędziowe $C$ , jako minimalne, składa się z gwiazd. A zatem, $M$ musi zawierać po dokładnie jednej krawędzi z każdej gwiazdy pokrycia $C$ . Istotnie, gdyby jakaś gwiazda nie zawierała krawędzi z $M$ , to $M$ nie byłoby maksymalne w sensie inkluzji, a gdyby w gwieździe były dwie krawędzie z $M^{'}$ ,to $M^{'}$ nie byłoby skojarzeniem. Tak więc $C$ składa się z $| M^{'} |$ gwiazd. Ponieważ w każdej gwieździe krawędzi jest o jedną mniej niż wierzchołków, to skojarzenie $M^{'}$ ma

| V (𝐆) | - | C | = | V (𝐆) | - ρ (𝐆) = ν (𝐆)

krawędzi, co kończy dowód.

Ćwiczenie 5

Udowodnij, że w grafie prostym $𝐆$ zachodzi:

ν (𝐆) \leq τ (𝐆) \leq 2 ν (𝐆)

Wskazówka

Niech $M$ będzie maksymalnym skojarzeniem, a $C$ minimalnym pokryciem wierzchołkowym w grafie $𝐆$ . Co możesz powiedzieć o związku skojarzenia $M$ z pokryciem $C$ . Ponadto, rozważ zbiór wszystkich wierzchołków incydentnych z którąś krawędzią z $M$ .

Rozwiązanie

Niech $M$ będzie maksymalnym skojarzeniem, a $C$ minimalnym pokryciem wierzchołkowym w grafie $𝐆$ . Oczywiście każda krawędź skojarzenia $M \subseteq E (𝐆)$ , tak jak i każda krawędź grafu $𝐆$ jest incydentna z jakimś wierzchołkiem z $C$ . Skoro jednak $M$ jest skojarzeniem, to różne krawędzie z $M$ nie mogą być incydentne z tym samym wierzchołkiem. A zatem:

ν (𝐆) = | M | \leq | C | = τ (𝐆)

Ponadto, każda krawędź $e \in E (𝐆)$ jest incydentna z jakimś wierzchołkiem ze zbioru $C^{'}$ składającego się ze wszystkich końców krawędzi skojarzenia $M$ . Istotnie, gdyby krawędź $e$ nie była incydentna z $C^{'}$ , to zbiór $M$ powiększony o $e$ przeczyłby o maksymalności skojarzenia $M$ . A zatem $C^{'}$ jest pokryciem wierzchołkowym. Z każdej krawędzi $C^{'}$ otrzymał po dwa wierzchołki, więc

τ (𝐆) \leq | C^{'} | = 2 | M | = 2 ν (𝐆)

Ćwiczenie 6

Udowodnij, że w grafie dwudzielnym $𝐆$ bez wierzchołków izolowanych zachodzi $ρ (𝐆) = α (𝐆)$ .

Wskazówka

Rozwiązanie

Na mocy Twierdzenia Koniga:

τ (𝐆) = ν (𝐆)

Z kolei Twierdzenie Gallai daje:

\begin{aligned} τ (𝐆) & = | V (𝐆) | - α (𝐆), \\ ν (𝐆) & = | V (𝐆) | - ρ (𝐆) . \end{aligned}

A zatem:

| V (𝐆) | - α (𝐆) = | V (𝐆) | - ρ (𝐆)

,

czyli

ρ (𝐆) = α (𝐆) .

Matematyka dyskretna 2/Ćwiczenia 1: Zagadnienia Mini-Maksowe w grafach

Zagadnienia Mini-Maksowe w grafach

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia