Języki, automaty i obliczenia/Ćwiczenia 5: Algorytmy konstrukcji automatu minimalnego
Ćwiczenia 5
Ćwiczenie 1
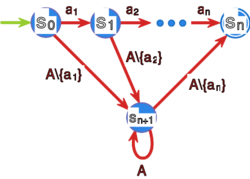
Ile co najmniej stanów ma automat akceptujący dokładnie jedno słowo o długości ?
Ćwiczenie 2
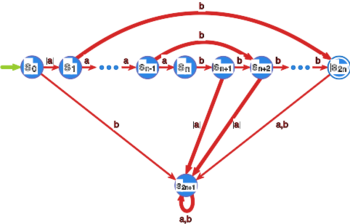
Niech będzie dowolną, ustaloną liczbą. Wykaż, że automat rozpoznający język
ma co najmniej stany.
Ćwiczenie 3
Niech będzie automatem minimalnym dla automatu . Czy zbiór stanów automatu minimalnego obliczonego za pomocą algorytmu wyznaczania stanów rozróżnialnych, zależy od:
- (1) wyboru w stanu początkowego ,
- (2) wyboru w zbioru stanów końcowych ?
Ćwiczenie 4
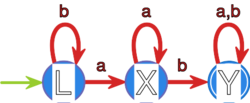
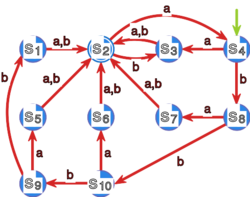
Zastosuj algorytm wyznaczający stany rozróżnialne do
zminimalizowania następujących automatów: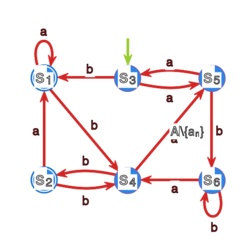 |
 |
Ćwiczenie 5
Wykorzystując algorytm stabilizujących się relacji wyznacz automaty minimalne dla automatów z rysunków 3 oraz 4.
Ćwiczenie 6
Niech , gdzie . Zastosuj algorytm wykorzystujący pochodną Brzozowskiego do obliczenia automatu minimalnego dla tego języka.
Poniżej znajduje się opis jeszcze jednego algorytmu minimalizacji - algorytmu Hopcrofta. Jest on nieco bardziej skomplikowany niż trzy podane dotychczas algorytmy, ale posiada lepszą złożoność niż algorytm obliczania stanów rozróżnialnych czy też algorytm wyznaczania ciągu relacji stabilizujących. Przeanalizuj opis algorytmu i jego zapis, a następnie rozwiąż zadanie 7.
Niech będzie automatem, a podzbiorem. Dowolny podzbiór i dowolna litera wyznaczają na zbiorze relację równoważności o dwóch klasach abstrakcji:
przy czym jeśli jeden ze zbiorów jest pusty, to relacja ta posiada tylko jedną klasę abstrakcji. Wprost z definicji zbiory i tworzą podział zbioru (tzn. ).Oznaczmy omawianą relację przez .
W algorytmie zmienna oznacza podział zbioru stanów , a - listę par , które będą wykorzystane do definiowania kolejnych relacji .
Algorytm MinHopcroft - algorytm Hopcrofta minimalizacji automatu
1 Wejście: - automat taki, że 2 Wyjście: - podział zbioru przez prawą kongruencję automatową 3 ; jest zbiorem rozłącznych podzbiorów 4 if then 5 for each do 6 włóż; 7 end for 8 else 9 for each do 10 włóż ; 11 end for 12 end if 13 while do 14 zdejmij ; 15 ; 16 for each do 17 for each do 18 ; zawiera dwie klasy abstrakcji 19 ; 20 if then 21 ; zdejmij z dokładnie parę 22 włóż; 23 włóż; 24 else 25 if then 26 włóż; 27 else 28 włóż; 29 end if 30 end if 31 end for 32 end for 33 end while 34 return ;
Funkcja zdejmij() pobiera z listy
dowolny element i zwraca go jako swoją wartość. Procedura włóż() dodaje do listy element .
Aby zdefiniować funkcję przejść automatu minimalnego, jego zbiór stanów końcowych oraz stan początkowy, należy postąpić identycznie jak w algorytmie wyznaczania ciągu stabilizujących się relacji. Jedyna różnica polega na tym, że w miejsce relacji otrzymaliśmy podział zbioru na klasy abstrakcji zadane przez poszukiwaną relację. Oczywiście klasy abstrakcji wyznaczają jednoznacznie relację równoważności i na odwrót - relacja równoważności wyznacza jednoznacznie podział zbioru na klasy równoważności, zatem forma opisu relacji przez klasy abstrakcji nie stanowi dla nas żadnego problemu.
Przy właściwej reprezentacji wszystkich używanych struktur, algorytm MinHopCroft działa w czasie , gdzie jest liczbą stanów automatu, a rozmiarem jego alfabetu wejściowego. Wyjściem algorytmu jest podział zbioru stanów. Każdy element zbioru reprezentuje jeden stan automatu minimalnego.
Ćwiczenie 7
Zastosuj algorytm Hopcrofta do zminimalizowania automatu z rysunku 3 (patrz cwiczenie 4.)
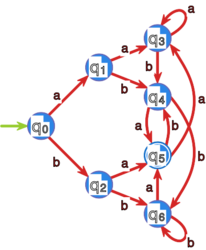
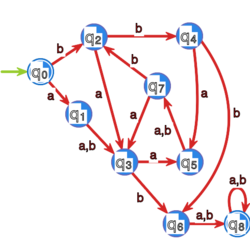
Ćwiczenie 8
Zminimalizuj przedstawione poniżej automaty:
- (1) stosując algorytm wyznaczający stany rozróżnialne,
- (2) stosując algorytm stabilizujących się relacji,
- (3) stosując algorytm Hopcrofta.
 |
 |
Ćwiczenie 9
Niech , gdzie . Zastosuj algorytm wykorzystujący pochodną Brzozowskiego do obliczenia automatu minimalnego dla tego języka.