Matematyka dyskretna 1/Test 15: Metody algebraiczne w teorii grafów
Niech oznacza liczbę skierowanych marszrut, nie dłuższych niż , z wierzchołka do w grafie skierowanym , a niech będzie macierzą . Wtedy:
wtedy i tylko wtedy, gdy
Zaznacz prawdziwe zależności dla grafu prostego
o macierzy sąsiedztwa ,
macierzy incydencji ,
zorientowanej macierzy incydencji
oraz macierzy stopni :
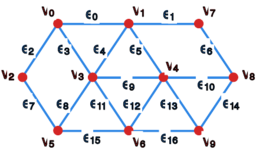
Niech będzie grafem o wierzchołkach przedstawionym na Rysunku 1, a macierz , o rozmiarach , będzie minorem (podmacierzą) zorientowanej macierzy incydencji , w którym kolumny odpowiadają krawędziom .
Wtedy:
macierz jest nieosobliwa
macierz jest osobliwa
suma elementów w każdej kolumnie macierzy wynosi
macierz jest antysymetryczna
Na to by permanent grafu był niezerowy, wystarcza by:
graf posiadał cykl Hamiltona
graf posiadał cykl Eulera
graf był spójny
graf był grafem dwudzielnym posiadającym skojarzenie doskonałe
Zaznacz zdania prawdziwe o wartościach własnych grafów:
Co najmniej jedna z wartości własnych jest liczbą zespoloną.
Jeśli wszystkie wartości własne są wymierne, to graf jest eulerowski.
Wszystkie wartości własne grafu hamiltonowskiego są rzeczywiste.
Wszystkie wartości własne dowolnego grafu są rzeczywiste.
Zaznacz prawdziwe związki wartości własnych z maksymalnym stopniem wierzchołka
w grafie prostym:
wtedy i tylko wtedy, gdy któraś spójna składowa grafu jest grafem regularnym stopnia
jest wartością własną macierzy wtedy i tylko wtedy, gdy jest regularnym grafem dwudzielnym stopnia
W grafie regularnym o wierzchołkach stopnia
oraz wartościach własnych i
moc niezależnego podzbioru jest ograniczona z góry przez:
Zaznacz zdania prawdziwe wiążące liczbę chromatyczną
z wartościami własnymi grafu regularnego :