GKIW Moduł 6a

Komputerowe wspomaganie projektowania jest dziedziną stosunkowo nową, ale szeroko wykorzystywaną przez różnych specjalistów. Różnorakie zastosowania wymagają definicji – opisu reprezentacji różnych obiektów. Z jednej strony typowe obiekty mechaniczne czy architektoniczne, z drugiej efekty specjalne filmów science fiction, gdzie jedynym ograniczeniem jest wyobraźnia twórców. Z drugiej strony systemy wspomagania projektowania dają dodatkowe możliwości wykonywania wielu obliczeń związanych bezpośrednio z dziedziną zastosowania – obliczeń konstrukcyjnych czy wytrzymałościowych. Oczywiście grafika komputerowa daje możliwość zobaczenia projektu – możliwość wizualizacji wyobrażeń projektanta. Niezbędne staje się narzędzie do modelowania kształtu – obiektu, powierzchni. Warto zwrócić uwagę na fakt, że użytkownicy takich systemów reprezentują różne poziomy przygotowania informatycznego. System modelowania powinien być więc prosty i efektywny, powinien dawać możliwość definicji kształtu za pomocą minimalnej liczby parametrów, a modyfikacja kształtu powinna dotyczyć wybranego fragmentu, a nie całości krzywej czy powierzchni.

W latach sześćdziesiątych XX wieku w fabryce Renault rozpoczął pracę pierwszy system modelowania geometrycznego na użytek komputerowego wspomagania projektowania. Twórcą tego systemu był P. Bézier – będący jedną z najważniejszych postaci w tej dziedzinie. Dzisiaj każda fabryka samochodów projektuje kształty karoserii wykorzystując modelowanie geometryczne.

Istnieje wiele metod modelowania krzywych i powierzchni. Mają one różne właściwości i wymagają osobnego omówienia.

Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą – najprościej wielomianową. Jeżeli dany jest ciąg parami różnych liczb Parser nie mógł rozpoznać (błąd składni): {\displaystyle t_0, t_1, t_2, …t_n } – węzłów interpolacyjnych i odpowiadających im punktom Parser nie mógł rozpoznać (błąd składni): {\displaystyle P_0, P_1, P_2,…P_n.} To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci:

$P (t) = Σ_{i = 0}^{n} P_{i} (\prod_{j = 0 j \neq i}^{n} \frac{t - t_{j}}{t_{i} - t_{j}})$

Dla małej liczby punktów (kilku) uzyskana krzywa zachowuje się zgodnie z oczekiwaniem. Niestety dla większej liczby punktów – krzywa wykazuje bardzo dużą wrażliwość na zaburzenia węzłów i skłonność do oscylacji – co pokazuje rysunek a). Dodatkowo każdy fragment krzywej zależy od wszystkich węzłów – brak jest lokalnej reprezentacji. Problem oscylacji można rozwiązać korzystając z interpolacji krzywą sklejaną – przedziałami wielomianową niskiego stopnia, rysunek b). Jednak w obu przypadkach kontrola nad kształtem krzywej pomiędzy węzłami jest trudna. Wady te powodują, że takie rozwiązanie jest praktycznie nieprzydatne.

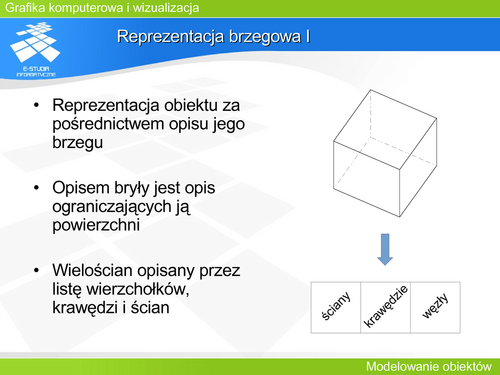
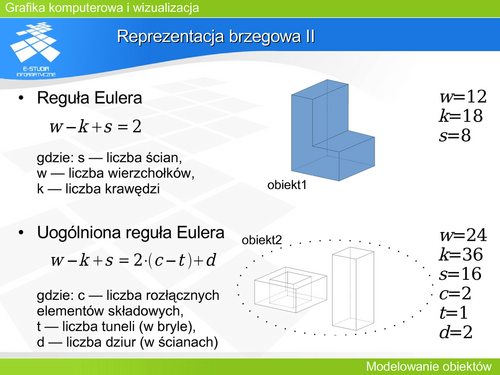
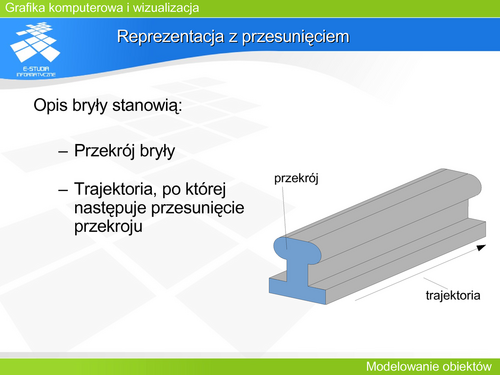
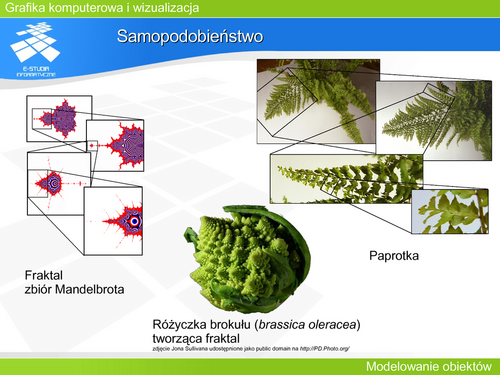
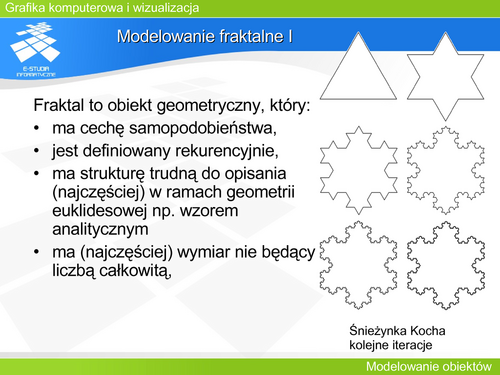
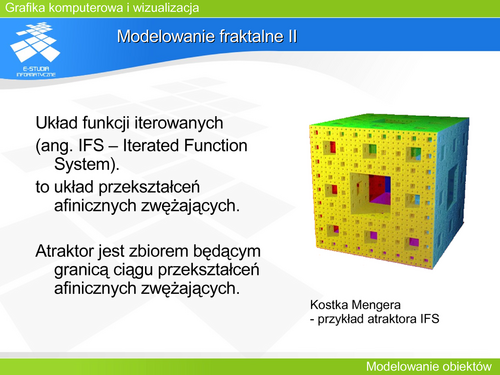
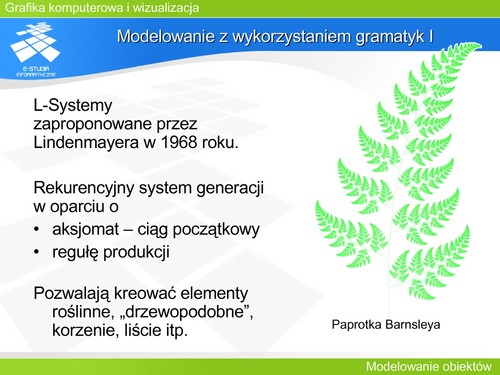
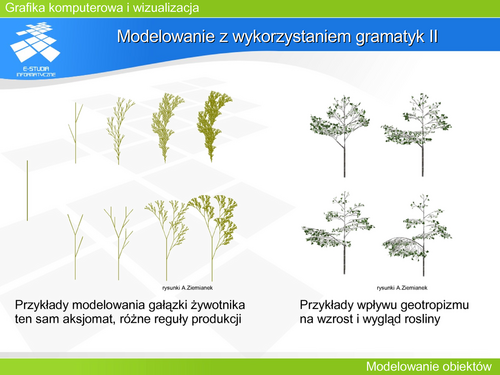
Wiele krzywych jest opisanych równaniem uwikłanym. Taka reprezentacja nie daje możliwości kontroli konkretnego fragmentu krzywej.

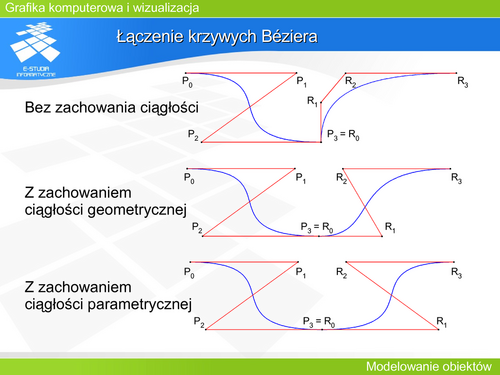
Wygodnym sposobem opisu krzywych i powierzchni jest opis parametryczny. W tym przypadku za pomocą doboru wartości parametru można zdefiniować dowolny fragment krzywej, a kierunek wzrostu parametru jednoznacznie określa np. kierunki stycznych połączonych fragmentów. Przykładowa czterolistna koniczynka jest narysowana na rysunku a) w postaci rozety czterolistnej :

$x (t) = a \cdot s i n (1 \cdot t) \cdot c o s (t)$ $y (t) = a \cdot s i n (1 \cdot t) \cdot s i n (t)$

dla

$a > 0, 0 < t < 2 π$

Na rysunku b) w postaci hipotrochoidy:

$x (t) = (R + r) c o s (t) - λ r c o s (\frac{R + r}{r} t)$

$y (t) = (R + r) s i n (t) - λ r s i n (\frac{R + r}{r} t)$

dla

$R > 0, r < 0, λ > 1, 0 < t < 2 < 2 π$

Często wykorzystywanymi powierzchniami są powierzchnie drugiego stopnia. Ich równanie uwikłane ma postać:

$f (x, y, z) = P^{T} Q P = 0$

gdzie Q jest macierzą współczynników postaci

$Q = [\begin{matrix} A & D & F & G \\ D & B & E & H \\ F & E & C & J \\ G & H & J & K \end{matrix}]$

oraz

$P = [\begin{matrix} x & y & z & 1 \end{matrix}]$

Przy czym dla każdej powierzchni drugiego stopnia jest znana reprezentacja parametryczna. Dla przykładowej hiperboloidy jednopowłokowej z prezentowanego rysunku:

Zalety stosowania powierzchni drugiego stopnia: Możliwość łatwego wyznaczenia wektora normalnego

Parser nie mógł rozpoznać (nieznana funkcja „\cec”): {\displaystyle \cec N= [\frac{\delta f}{\delta x} \frac{\delta f}{\delta y} \frac{\delta f}{\delta z}]}

Możliwość szybkiego wyznaczenia przecięcia powierzchni z prostą – efektywność stosowania w algorytmach związanych z metodą śledzenia promieni. Możliwość szybkiego wyznaczenia z na podstawie x i y – przydatne w algorytmach eliminacji elementów zasłoniętych.

Wielomiany Bernsteina są funkcjami bazowymi dla krzywych Béziera. Ich właściwości mają decydujący wpływ na właściwości krzywych.

Rysunek przedstawia wykresy wielomianów Bernsteina 2, 3, 4 i 5 stopnia. Najczęściej mamy do czynienia z wielomianami stopnia 3. W tym przypadku:

$B_{0, 3} (t) = (1 - t)^{3}, B_{1, 3} (t) = 3 t (1 - t)^{2}, B_{2, 3} (t) = 3 t^{2} (1 - t), B_{3, 3} (t) = t^{3}$

Ostatnia właściwość (zależność rekurencyjna) prowadzi do algorytmu wyznaczania punktów na krzywej bazującej na wielomianach Bernsteina.

Krzywa Béziera zawdzięcza swą nazwę Pierre’owi Bézierowi, warto jednak pamiętać,

że rozwiązanie to miało dwóch niezależnych twórców. Drugim był P. de Casteljau. Jego nazwiskiem został opatrzony podstawowy algorytm wyznaczania punktu krzywej. Krzywa Béziera stopnia n jest definiowana przez n+1 punktów Parser nie mógł rozpoznać (błąd składni): {\displaystyle P_0, P_1, P_2,…P_n} w bazie wielomianów Bernsteina. Jest to krzywa gładka, której kształt zależy od położenia punktów kontrolnych. Najczęściej stosowane są krzywe stopnia 3. Użytkownicy komputerów spotykają się z nią na co dzień w postaci fontów, których kształt jest projektowany właśnie z jej wykorzystaniem

Krzywa Béziera interpoluje dwa końcowe punkty kontrolne i aproksymuje pozostałe. Oznacza to, że dla krzywej stopnia 3 , jeśli ustalone są punkty końcowe (a tak jest najczęściej), to dwa pozostałe punkty decydują o kształcie.

Wady: - Brak możliwości reprezentacji krzywych stożkowych. - Zmiana reprezentacji krzywej po rzutowaniu perspektywicznym.

Korzystając z właściwości rekurencyjnej wielomianów Bernsteina można wyznaczyć punkty krzywej Béziera.

Algorytm de Casteljau wyznaczania punktu leżącego na krzywej Béziera na podstawie ciągu punktów kontrolnych Parser nie mógł rozpoznać (błąd składni): {\displaystyle P_0, P_1, P_2,…P_n}

for i:= 0 to n do Pi,0 = Pi;
for j:=1 to n do 
for i:=j to n  do
Pi,j := (1-t)*Pi-1,j-1 + t*Pi,j-1;

Jeśli zadaniem jest wyznaczenie dużej liczby punktów leżących na krzywej Béziera to tańszym obliczeniowo rozwiązaniem będzie przejście w wielomianach Bernsteina do postaci naturalnej wielomianu i obliczanie jego wartości algorytmem Hornera.

</math>

GKIW Moduł 6a

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia