MO Moduł 3

---

---

Funkcja oceny jest tu liniowa, bo jest oczywiste, że dodanie do niej dowolnej liczby nie zmienia rozważań (zmienia wartość funkcji wyboru w punkcie minimalizującym, która jest oczywiście od tej liczby zależna, ale rozwiązaniem zadania jest punkt minimalizujący, który jest taki sam !).

---

Zamiast „przy ograniczeniach” będziemy pisali $\mathrm{p}\mathrm{.}\mathrm{o}\mathrm{.}$

---

Z rysunku wynika, że ograniczenie (c) nie jest potrzebne, oraz że zbiór dopuszczalny jest wielokątem. Linie poziomicowe funkcji liniowej to proste, zatem rozwiązanie leży w wierzchołku wielokąta (albo rozwiązań jest wiele i leżą na brzegu wielokąta, gdy poziomice są równoległe do stosownego ograniczenia).

---

W przestrzeni zmiennych zadania liniowego optymalizacji zbiór dopuszczalny to (hiper)wielościan, miejscem geometrycznym stałej wartości funkcji celu jest (hiper)-płaszczyzna, a rozwiązanie zadania (o ile istnieje) leży w jego wierzchołku albo rozwiązań jest wiele i leżą na brzegu wielościanu albo na jego ścianie.

---

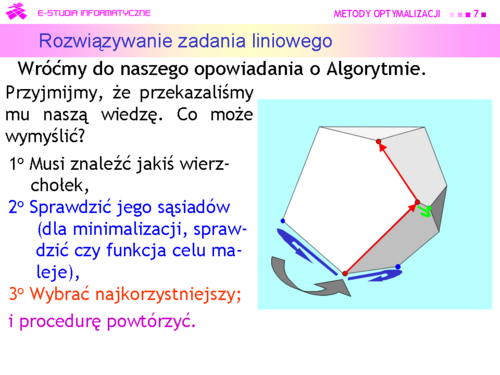Na płaszczyźnie taki algorytm będzie działać, bo każdy wierzchołek ma tylko dwu sąsiadów, ale przy większej liczbie wymiarów będzie to bardzo powolne i nie wiadomo, czy algorytm się nie zapętli.

---

W Polsce, nie bardzo wiadomo dlaczego, algorytm Dantziga nazywa się metodą sympleks, simpleksową, a nawet metodą sympleksów. Używane w matematyce pojęcie sympleksu nie ma nic wspólnego z metodą Simplex.

---

---

---

---

---

---

---

Dla równania$Ax=b,$ gdzie $x$ jest wektorem $n$ wymiarowym, a $b$ wektorem $p$ wymiarowym, macierzą bazową nazywa się każdą kwadratową nieosobliwą macierz $B$, którą da się utworzyć z $p$ kolumn macierzy $A$.

---

---

---

---

---

---

---

---

---

---

Główne problemy implementacyjne związane są z szybkością i dokładnością tego algorytmu. Najwięcej kłopotów jest w nim z odwracaniem kolejnych macierzy bazowych. Przypominamy, że numerycznie macierz odwraca się drogą faktoryzacji.

---

Uznane pakiety komercyjne zawierające algorytm Simplex to np. CPLEX, MINOS, NAG, AMPL, MATLAB i Mathematica

---

---

---

---

---

---

---

---