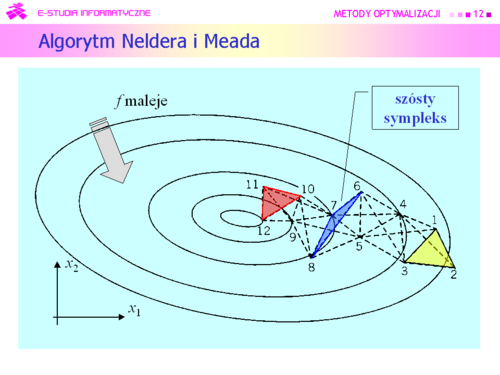
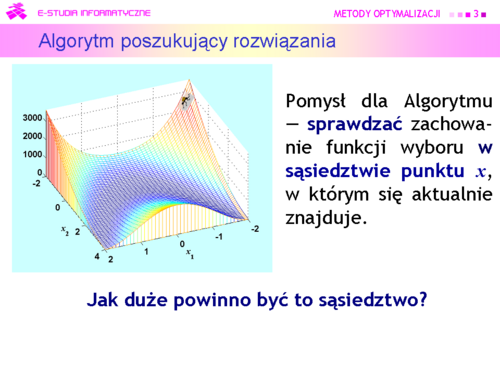
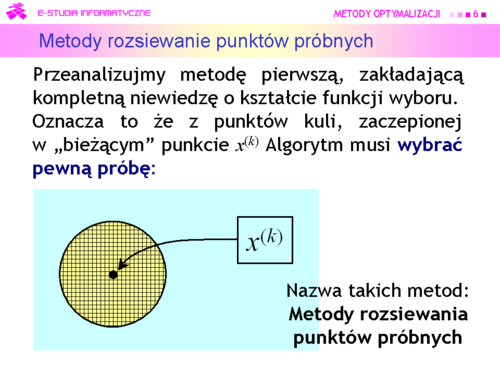
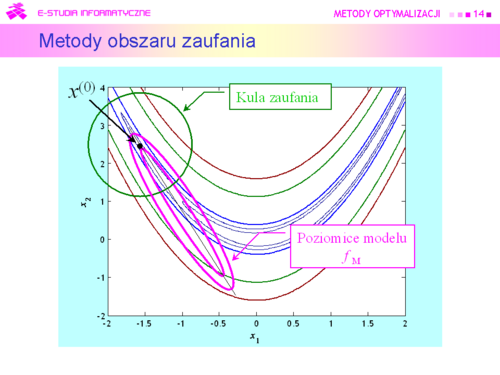
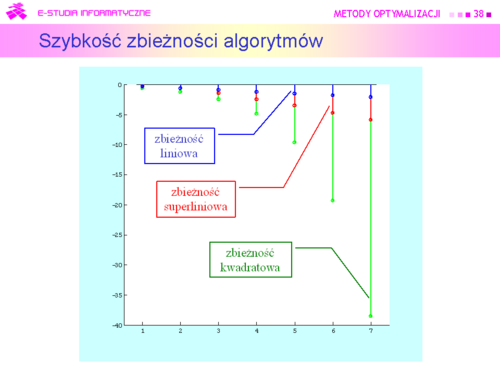
| Zbieżny ciąg otrzymany w kolejnych krokach algorytmu, jest zbieżny
a) liniowo, gdy dodatkowo
Parser nie mógł rozpoznać (błąd składni): {\displaystyle \frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty} \rho\>0}
b) superliniowo, gdy dodatkowo
c) kwadratowo, gdy dodatkowo
Definicje szybkości związane są z szybkością zbiegania do zera:
postępu geometrycznego o dodatnim ilorazie mniejszym niż jeden, np. danego wzorem
Parser nie mógł rozpoznać (błąd składni): {\displaystyle h^{(k)}=2^{-k} (\frac{2^{-(k+1)}}{2^{-k}}=\frac{1}{2}\ge 0) – zbieżność liniowa,}
np. ciągu danego wzorem
Parser nie mógł rozpoznać (błąd składni): {\displaystyle h^{(k)}=k^{-k},k\in 1 \infty (\frac{k^{-(k+1)}}{k^k}=\frac{1}{k}\rightarrow 0) – zbieżność superliniowa,}
np. ciągu danego wzorem
Parser nie mógł rozpoznać (błąd składni): {\displaystyle h^{(k)}=2^{-k},k\in 1 \infty (\frac{2^{-2^{k+1}}}{(2^{-2^k})^2}\rightarrow 0)– zbieżność kwadratowa.}
|