GKIW Moduł 3
|
|
Tworzenie obrazu na monitorze lub urządzeniu drukującym wymaga wypełnienia wybranego obszaru pikseli określonymi barwami w taki sposób, aby powstał zamierzony rysunek. Korzystając z edytora graficznego wybieramy pewne obiekty podstawowe – tak zwane prymitywy (np. odcinek) i żądamy narysowania ich w określonym miejscu. Nie zastanawiamy się w tym momencie nad tym, że żądanie to, z pozoru bardzo proste, wymaga rozwiązanie wielu problemów geometrycznych oraz opracowania skutecznych i szybkich algorytmów. I to bez względu na to czy będzie to realizowane przez odpowiednią bibliotekę czy tez sprzętowo przez kartę graficzną |
|
Jednym z podstawowych problemów tego typu jest zadanie narysowania odcinka na mapie pikseli. Najprostszym rozwiązaniem wydaje się poprowadzenie prostej przez końce odcinka i opisanie jej równaniem . Następnie wyznaczenie wartości dla całkowitych wartości odpowiadających kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne do wartości całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek tzn. , gdzie jest operacją zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania, zaokrąglania). |
|
Rozwiązanie oparte w całości na arytmetyce stałopozycyjnej zaproponował Bresenham w 1965 roku. Jest to algorytm przyrostowy, w którym jedna współrzędna np. x wzrasta w każdym kroku o 1, tzn. . Bez zmniejszania ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka od 0 do 1. (Jest to 1/8 układu współrzędnych. Dla innych wartości można bowiem odpowiednio zamienić zmienne lub znaki przed nimi.) Wzrost y w takim przypadku zależy od wyboru piksela (S lub T), który jest bliżej teoretycznej prostej. O wyborze decyduje zmienna kontrolna d, która jest uaktualniana w każdym kroku. |
|
Pełny algorytm Bresenhama dla x2>x1, y2>y1, 0<m<1 wyglądałby tak:
procedure Bresline (x1,x2, y2,y2,) begin
end Algorytm taki wykorzystujący tylko operacje całkowite jest również użyteczny w rozwiązaniach sprzętowych. |
|
Niestety korzystanie z rastra również i w przypadku rysowania odcinka może prowadzić do pewnych problemów.
Pierwszym jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla d=0 w zależności od wzrostu lub spadku wartości współrzędnych. Poważniejszym problemem jest zmiana jasności. Oba odcinki na rysunku składają się z 7 punktów. Tylko że odcinek po przekątnej rastra jest razy dłuższy od odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra i podobnie jak usuwanie wrażenia schodków odcinka rozwiązuje się go zmieniając barwy pikseli sąsiednich. |
|
Na podobnej zasadzie jak rysowanie odcinka, Bresenham opracował algorytm rysowania łuku okręgu. Oczywiście zmieniają się w tym przypadku warunki wyboru pikseli, ale algorytm ten również wykorzystuje tylko operacje na liczbach całkowitych.
Przy okazji rysowania okręgu warto zwrócić uwagę na parametr charakteryzujący proporcje boków rastra pikseli w pionie i w poziomie, czyli aspekt. Jeśli proporcje rozdzielczości dla kart graficznych 1024x768 wynoszą 4:3, natomiast 1280x1024 wynoszą 5:4, to jeśli chcemy wyświetlić takie obrazy na tym samym monitorze, to proporcje trzeba przeliczyć także w odległości między pikselami. Inaczej narysowany okrąg albo w jednym albo w drugim przypadku będzie miał kształt elipsy. |
|
Wypełnianie obszaru jest drugim po rysowaniu odcinka lub łuku, najczęściej występującym problemem związanym z prymitywami. Zadanie dla szczególnych przypadków (np. dla prostokąta) jest zadaniem trywialnym. Natomiast w ogólnym przypadku algorytm powinien pracować poprawnie dla dowolnego wielokąta (także wklęsłego), również dla wielokątów z „dziurami”. |
|
Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne. Algorytm rozwiązujący jedno z nich może posłużyć do rozwiązania drugiego. |
|
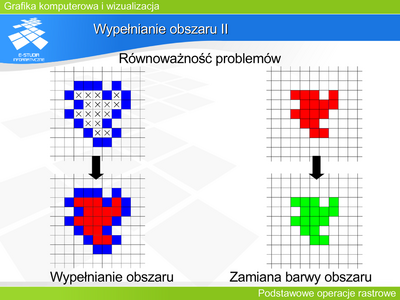
Można zauważyć, że jeśli wybierzemy jeden punkt, który jest wewnątrz wypełnianego obszaru, to punkt sąsiedni będzie również punktem wewnątrz albo będzie punktem brzegowym.
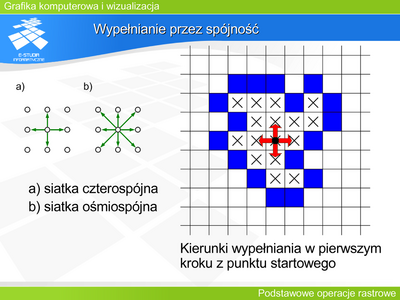
Wypełnianie przez spójność zakłada znajomość punktu startowego (tzw. „ziarna”) wewnątrz obszaru. Punkt ten jest wypełniany, a następnie startując z niego wypełniamy punkty sąsiednie (jeśli oczywiście istnieją – jeśli nie są już wypełnione, ani nie są punktami granicznymi obszaru). Jednocześnie punkty sąsiednie stają się wyjściowymi dla wypełniania w następnym kroku. Procedura ta jest powtarzana dopóki można wskazać punkty wyjściowe (niewypełnione) wewnątrz obszaru. Warto zwrócić tutaj uwagę na problem sąsiedztwa i konieczność dostosowania do niego kształtu brzegu. Można wyróżnić dwa przypadki. Gdy ruchy po mapie pikseli mogą odbywać się analogicznie do ruchów wieży po szachownicy – wtedy piksel ma 4 sąsiadów – siatka jest czterospójna. Gdy dodamy do tego jeszcze ruchy na ukos (odpowiada to kierunkom ruchów hetmana w szachach), to piksel ma 8 sąsiadów – siatka jest ośmiospójna. Czytelnik może przeanalizować jak powinien wyglądać rozkład pikseli brzegu dla obu przypadków aby stanowił on figurę zamkniętą z punktu widzenia możliwości ruchu. Algorytm wypełniania przez spójność dla siatki czterospójnej. Przyjęto: c_b – barwa brzegu, c_f – barwa wypełnienia procedure wypełnij1(x,y) begin
end Czytelnik może zaproponować korektę obejmującą siatkę ośmiospójną. Zaproponowana postać algorytmu wypełniania przez spójność jest algorytmem rekurencyjnym. Daje to łatwość opisu ale także problemy realizacyjne. Z tego powodu znane są wersje niniejszego algorytmu w postaci nierekurencyjnej. Algorytm wypełniania przez spójność jest czasem nazywany algorytmem przez sianie (punkt startowy jest „ziarnem”). |
|
Wypełnianie przez kontrolę parzystości wykorzystuje pewną właściwość przecięcia brzegu linią prostą. Jeśli punkty przecięcia ponumerujemy kolejnymi liczbami naturalnymi zgodnie z orientacją prostej (na rysunku od lewej do prawej dla prostej poziomej) i jeśli będziemy poruszać się po prostej zgodnie z jej orientacją to każde nieparzyste przecięcie będzie „wejściem” do wnętrza obszaru, natomiast każde parzyste będzie „wyjściem” na zewnątrz. Zatem, aby wypełnić obszar należy go przecięć prostymi odpowiadającymi kolejnym rzędom pikseli, a następnie wypełnić odcinkami pomiędzy każdym nieparzystym przecięciem, a najbliższym parzystym. |
|
Oczywiście należy zmodyfikować to postępowanie dla przypadków szczególnych, gdy punkt przecięcia jest jednocześnie lokalnym ekstremum brzegu, co zaburza prostą regułę parzystości. Lokalizacja lokalnego ekstremum możliwa jest na podstawie położenia końców przecinanych odcinków. Jeśli są po tej samej stronie prostej wypełniającej – przecinany punkt jest lokalnym ekstremum i nie należy jego liczyć przy analizie parzystości.
Na rysunku prosta l2 przecina wielokąt w wierzchołku (punkt 2) ale jest to przecięcie zwykłe – pozostałe końce przecinanych boków są po przeciwległych stronach prostej l2. Prosta l3 również przecina wielokąt w wierzchołku (punkt 2) ale jest to ekstremum lokalne – pozostałe końce boków są po tej samej stronie prostej l3. |
|
W szczególnych przypadkach mogą pojawić się obszary nie dające się wypełnić w sposób spójny – problem „drzazgi”. Jedynym sposobem rozwiązania tego problemu jest nadpróbkowanie. Należy spróbkować i wypełnić drzazgę z większą rozdzielczością, a następnie uśrednić barwę/luminancję wracając do rozdzielczości rastra. |
|
Większość rysowanych obiektów jest definiowana w rzeczywistym układzie kartezjańskim. Przedstawienie takiego obiektu na ekranie monitora (lub z wykorzystaniem innego urządzenia) wymaga określenia fragmentu, który jest obrazowany. Jeśli tylko część prymitywu jest zobrazowana, to oprócz algorytmu rysowania prymitywu jest potrzebny algorytm obcinania go do widocznego fragmentu. |
|
Algorytm Cohena-Sutherlanda (1974) służy do obcinania odcinków do prostokątnego okna. Oznacza to, że należy wybrać odcinki (lub ich fragmenty) do obcięcia na podstawie położenia ich końców.
Płaszczyzna została podzielona na 9 obszarów . Prostokąt centralny odpowiada obszarowi okna. Jednocześnie krawędzie okna wyznaczają cztery proste: prawą, lewą, górna i dolną. Każdemu obszarowi został przypisany czterobitowy kod. Kolejne bity kodu określają poziome i pionowe pasy. Operacja AND przeprowadzona na kodach końców odcinka pozwala odrzucić te odcinki, które na pewno są poza oknem. Spośród pozostałych odcinków należy wybrać te, które rzeczywiście mają wspólne punkty z oknem oraz przyciąć do jego rozmiaru. Operacja AND pozwala w tym przypadku wybrać prostą obcinającą. Jeśli wynik operacji AND jest różny od zera – należy odrzucić odcinek jako nie mający na pewno punktów wspólnych z oknem. Jeśli wynik operacji AND jest zerowy – odcinek może przecinać okno. W takiej sytuacji należy rozważyć przypadek szczególny gdy kody obu końców są zerowe (punkty P1 i K1 na rysunku), wtedy cały rysunek leży wewnątrz okna. Natomiast jeśli kody końców są niezerowe to określają one którymi prostymi należy przyciąć odcinek. Odcinek należy przyciąć prostą prawą (K2=0010). Odcinek prostymi lewą i dolną (P3=0101) oraz prawą i górną (K3=1010). |
|
W przypadku obcinania wielokąta, zastosowanie algorytmu obcinania odcinków przynosi tylko połowiczny sukces. Wielokąt tworzy bowiem zbiór uporządkowanych wierzchołków. Każdy wierzchołek jest początkiem pewnego boku i jednocześnie jest końcem poprzedniego boku w danym uporządkowaniu. Potraktowanie boków wielokąta jako zbioru odcinków i przycięcie ich powoduje, że tracimy informacje o ich połączeniach.
Przykładem algorytmu rozwiązującego ten problem jest algorytm Sutherlanda-Hodgmana obcinania wielokąta. Niech kolejne wierzchołki wielokąta tworzą listę cykliczną Obcinanie odbywa się kolejno dla prostych zawierających boki okna w ustalonym porządku – np. tak jak na rysunku zgodnie z ruchem wskazówek zegara poczynając od krawędzi lewej. W każdym kroku algorytmu rozpatrywany jest jeden wierzchołek leżący poza oknem przycinania. Wierzchołek taki jest usuwany z listy ale w jego miejsce wstawiane są wierzchołki „odpowiadające mu” na brzegu okna. Oczywiście należy wziąć pod uwagę również i takie przypadki, w których dodany wierzchołek będzie leżał na prostej zawierającej bok okna ale będzie to wierzchołek, który zostanie również usunięty np. w następnym kroku. Z drugiej strony możliwy jest także przypadek, kiedy kolejne wierzchołki wielokąta leżą na zewnątrz okna i wtedy kilka z nich może zostać zastąpionych jednym punktem na brzegu okna. |
|
Algorytm Cohena-Sutherlanda bardzo efektywnie klasyfikuje odcinki i jednocześnie jest bardzo prosty w implementacji. Powoduje to, że jest chyba najczęściej stosowanym algorytmem przycinania odcinków do prostokątnego okna.
Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne. W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu obcinania. Jeśli opiszemy prostą parametrycznie to wzrost parametru określi naturalny zwrot prostej. Niech punkty P0 i Pk odpowiadają odpowiednio parametrom t=0 i t=tk dla k>0. Wektor określa zwrot prostej. Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego (skierowanego na zewnątrz) do boku wielokąta. Jeśli to parametr tk określa punkt Pk.który może być „maksymalnym” punktem przecięcia z wielokątem (np. punkt dla t=t2 na rysunku). Jeśli to parametr tk określa punkt Pk.który może być „minimalnym” punktem przecięcia z wielokątem (np. punkt dla t=t1 na rysunku). Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego wielokąta. Algorytm ten został w 1984 roku rozszerzony Lianga i Barsky’ego do ogólnego przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D obcinania płaszczyznami prostopadłymi do osi układu współrzędnych. |
|
Geometria obliczeniowa (ang. computational geometry) jest stosunkowo nową dziedziną informatyki. Z jednej strony jest często traktowana jako narzędzie niezbędne do realizacji algorytmów w grafice komputerowej, z drugiej pozwoliła również wprowadzić do grafiki nowe struktury danych lub je usystematyzować. Niektóre zagadnienia takie jak wyznaczenie wypukłej otoczki zbioru punktów (wypukłej skorupki) albo triangulacja wielokąta stanowią samodzielne problemy geometrii obliczeniowej i Czytelnik może znaleźć ich rozwiązania w podręcznikach z tej dziedziny. |
|
Częstym problemem jest konieczność uporządkowania punktów w układzie biegunowym. Wyznaczenie kąta na podstawie współrzędnych kartezjańskich wymagałoby użycia funkcji trygonometrycznych, co znacznie spowalniałoby rozwiązanie zadania. Funkcja alfa daje możliwość porównania kątów bez wyznaczania ich wartości. Należy jednak pamiętać, że wartość funkcji alfa nie jest liniowo związana z wartością kąta i próba szacowania kąta na tej podstawie byłaby poważnym błędem. |
|
Drugim zagadnieniem, które często występuje jest określenie zorientowania trójki punktów na płaszczyźnie. Zadanie to ma oczywiście eleganckie rozwiązanie w postaci wektorowej. Wystarczy wyznaczyć dwa wektory rozpięte na badanych trzech punktach, a następnie obliczyć ich iloczyn wektorowy. Zwrot wektora wynikowego określi poszukiwane zorientowanie.
Zastosowanie macierzy współrzędnych (przez analogię do macierzy określającej iloczyn wektorowy) upraszcza obliczenia. Jeśli det M > 0 mówimy o dodatnim zorientowaniu (lewoskrętnym lub przeciwnym do ruchu wskazówek zegara). Jeśli det M < 0 mówimy o ujemnym zorientowaniu (prawoskrętnym lub zgodnym z ruchem wskazówek zegara). |
|
Zagadnienie sprawdzenia przynależności punktu do wnętrza wielokąta ma bardzo proste rozwiązanie dla wielokąta wypukłego. Jeśli wziąć pod uwagę prostą wyznaczoną przez dwa kolejne wierzchołki wielokąta, to prosta ta dzieli płaszczyznę na dwie półpłaszczyzny, z których tylko jedna zawiera wielokąt. Podstawiając więc współrzędne badanego punktu do równania prostej można na podstawie znaku równania stwierdzić po której stronie prostej punkt się znajduje. A zatem punkt P1 na rysunku będzie po tej samej stronie prostej wyznaczonej przez V1 V2 co np. wierzchołek V4. Natomiast punkty P2 i V4 będą po przeciwnych stronach tej prostej.
Algorytm sprawdzania przynależności punktu do wnętrza wielokąta wypukłego jest następujący.
Opisany algorytm należy w zależności od potrzeb uzupełnić o analizę samego wielokąta (przynależność lub nie do odpowiednich odcinków co jest zabiegiem technicznym i nie stanowi problemu. Podstawową wadą zaprezentowanego algorytmu jest fakt, że działa poprawnie tylko dla wielokątów wypukłych. Dla wielokątów wklęsłych będą proste wyznaczone przez kolejne wierzchołki, które będą przecinały wielokąt. Dla wielokątów dowolnych problem rozwiązuje się algorytmem kontroli parzystości lub algorytmem analizy sumy katów zorientowanych. Warto przy tym zwrócić uwagę, że rozpatrywane są tylko wielokąty zwykłe, to znaczy takie, których krawędzie nie mają punktów wspólnych poza wierzchołkami. |
|
Przez analogię do wypełniania wielokąta przez kontrolę parzystości na rastrze pikseli można zaproponować algorytm sprawdzania przynależności punktu do wielokąta. Jeśli z badanego punktu poprowadzimy półprostą (w dowolnym kierunku – z punktu widzenia kierunków układu współrzędnych wygodna będzie np. półprosta pozioma), to może ona przeciąć wielokąt. Jeśli liczba przecięć z bokami wielokąta jest nieparzysta to punkt leży wewnątrz wielokąta (punkt P1 na rysunku). Jeśli liczba przecięć jest parzysta, to punkt jest na zewnątrz (punkt P2 na rysunku).
Algorytm jest bardzo prosty, jednak pamiętając o problemach ze szczególnymi przypadkami w algorytmie wypełniania przez kontrolę parzystości, należy przypuszczać, że podobne sytuacje wystąpią i tutaj. Oczywiście rozwiązanie jest również analogiczne .Do algorytmu należy dodać dwa warunki. Jeśli punkt przecięcia jest ekstremum lokalnym, to liczymy go podwójnie. Jeśli półprosta zawiera cały bok wielokąta, to traktujemy to jako jeden pseudo-wierzchołek. |
|
Drugim rozwiązaniem problemu sprawdzenia przynależności punktu do wielokąta jest analiza kątów.
Można założyć, że wierzchołki wielokąta są uporządkowane przeciwnie do ruchu wskazówek zegara. Z badanego punktu przez każdy wierzchołek wielokąta prowadzimy półprostą. Badany punkt oraz półproste przechodzące przez kolejne wierzchołki wyznaczają kąt, któremu można przypisać zorientowanie analogicznie jak zorientowanie wielokąta (+ jeśli kolejność ramion kąta jest przeciwna do ruchu wskazówek zegara, i – w sytuacji odwrotnej). Po przyjęciu takich założeń wystarczy zsumować wszystkie kąty związane z punktem badanym. Jeśli to punkt jest wewnątrz wielokąta. Jeśli to na zewnątrz. Oczywiście należy pamiętać o błędach zaokrąglenia i oczekiwanie np. dokładnie zerowej wartości byłoby nieporozumieniem. Jeśli jesteśmy pewni że w implementacji nie ma błędu, to warunki można postawić jako: i . |
|
