PF Moduł 14

Wykład 14 - Zjawiska elektromagnetyczne 14.1. Zjawisko indukcji elektromagnetycznej 14.2. Zjawisko samoindukcji 14.3 Energia pola magnetycznego 14.4. Elektromagnetyczne drgania swobodne 14.5. Elektromagnetyczne drgania tłumione 14.6. Elektromagnetyczne drgania wymuszone 14.7. Równania Maxwella w postaci całkowej 14.8. Operatory różniczkowe 14.9. Równania Maxwella w postaci różniczkowej 14.10-13. Materiały do ćwiczeń

---

14.1 Zjawisko indukcji elektromagnetycznej Zjawisko indukcji elektromagnetycznej odkryte przez Michaela Faradaya (1791-1867) polega na wzbudzaniu w zamkniętym obwodzie prądu indukcyjnego, pod wpływem zmian strumienia zewnętrznego pola magnetycznego. Bezpośrednią przyczyną przepływu prądu indukcyjnego jest powstająca w obwodzie siła elektromotoryczna $E=-\frac{d{\mathrm{\Phi }}_B}{dt}$ Reguła Lenza, określająca kierunek prądu indukcyjnego, wynika przede wszystkim z zasady zachowania energii. Przepływ prądu indukcyjnego jest oznaką, że w obwodzie pojawiła się energia. Zatem zmiana strumienia magnetycznego wymaga wykonania pracy przez siłę zewnętrzną, która tę zmianę wywołuje. Np. zbliżanie magnesu skierowanego biegunem N w stronę obwodu zwiększa strumień magnetyczny przenikający przez powierzchnię obwodu. Prąd indukcyjny popłynie w takim kierunku, żeby wytworzone przez niego pole magnetyczne odpychało zbliżający się magnes, a więc przed obwodem musi powstać biegun N. Reguła Lenza wynika również z bardzo ogólnej reguły przekory (Le Chatelier i Braun), która głosi, że układy fizyczne zachowują się przekornie. Układ fizyczny znajdujący się w stanie równowagii poddany działaniu czynnika zewnętrznego reaguje tak, żeby zmniejszyć wpływ tego czynnika ii osiągnać nowy stan równowagi możliwie niezbyt odległy od stanu równowagi wyjściowej. Zjawisko indukcji elektromagnetycznej jest jednym z wielu zjawisk fizycznych, których przebieg wynika z reguły przekory.

---

14.2 Zjawisko samoindukcji Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie $I(t)$ to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy $B(t)=\frac{{\mu }_0{\mu }_{r}N}{l}I(t)$ oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju ${\mathrm{\Phi }}_B(t)=B\cdot S=\frac{{\mu }_0{\mu }_{r}NS}{l}I(t)$ a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości $E_z=-\frac{d{\mathrm{\Phi }}_B}{dt}$ Zatem całkowita siła elektromotoryczna powstająca w zwojnicy $E=-N\frac{d{\mathrm{\Phi }}_B}{dt}$ Po podstawieniu i przekształceniu otrzymujemy wzór $E=-L\frac{dl}{dt}$ z którego wynika zależność wartości siły elektromotorycznej samoindukcji od szybkości zmiany natężenia prądu, oraz od indukcyjności zwojnicy $L=\frac{{\mu }_0{\mu }_r{N}^{2}S}{l}$ czyli współczynnika zależnego od parametrów zwojnicy, określającego zdolność zwojnicy do wytwarzania siły elektromotorycznej samoindukcji. Dużą wartość $L$ można uzyskać dla zwojnicy o dużej liczbie zwojów, z rdzeniem ferromagnetycznym (duża wartość ${\mu }_r$). Zjawisko samoindukcji może zachodzić w każdym obwodzie, w którym płynie prąd o zmieniającym się w czasie natężeniu. Indukcyjność $L$ obwodu zależy od kształtu i rozmiarów obwodu oraz od obecności materiału ferromagnetycznego.

---

14.3 Energia pola magnetycznego W chwili $t_0=0$ zamykamy klucz i w obwodzie RL zaczyna płynąć prąd o rosnącym natężeniu, spełniającym równanie $U_0-L\frac{dI}{dt}-RI=0$ którego rozwiązaniem jest funkcja $I(t)\frac{U_0}{R}(1-e^{-(t/\tau )})$ gdzie $\tau$ jest stałą czasową procesu narastania natężenia prądu do wartości wynikającej z prawa Ohma. Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez $I$ $U_{0}I=LI\frac{dI}{dt}+R{I}^2$ Iloczyn natężenia prądu i napięcia źródła $U_{0}I=P$ to moc źródła Składnik $R{I}^2=P_R$ to moc w oporniku. Zatem wyrażenie $LI\frac{dI}{dt}=P_B=\frac{d{W}_B}{dt}$ to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy. Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego wewnątrz zwojnicy $W_B=\frac{1}{2}L{I}^2$ Wykorzystując wzory $L=\frac{{\mu }_0{\mu }_r{N}^{2}S}{l}$ $B=\frac{{\mu }_0{\mu }_{r}N}{l}I$ otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej $W_B=\frac{1}{2}\frac{1}{{\mu }_0{\mu }_r}{B}^{2}V$ gdzie $V$ jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego $\frac{W_B}{V}=\frac{1}{2}\frac{1}{{\mu }_0{\mu }_r}{B}^2$ $w_B=\frac{1}{2}\overrightarrow{H}\cdot \overrightarrow{B}$

---

14.4 Elektromagnetyczne drgania swobodne Modelowym układem fizycznym, w którym zachodzić mogą elektromagnetyczne drgania harmoniczne swobodne jest zamknięty obwód elektryczny o oporności równej zeru, zawierający zwojnicę o indukcyjności $L$ i kondensator o pojemności $C$. W obwodzie przedstawionym na rysunku kondensator został naładowany ładunkiem $q_0$. Gdy w chwili $t=0$ zamkniemy obwód, to kondensator zacznie się rozładowywać i zmieniający się prąd rozładowania spowoduje powstanie w zwojnicy siły elektromotorycznej samoindukcji. Stan fizyczny obwodu można opisać za pomocą II prawa Kirchhoffa: $L\frac{dI}{dt}+\frac{q}{C}=0$ gdzie $I=\frac{dq}{dt}$ Po podstawieniach i przekształceniach otrzymujemy równanie elektromagnetycznego oscylatora harmonicznego swobodnego $\frac{d^{2}q}{d{t}^2}=-\frac{1}{LC}q$ Rozwiązaniem tego równania, spełniającym warunki początkowe: $q(0)=q_0$ , $I(0)=0$ jest funkcja Parser nie mógł rozpoznać (nieznana funkcja „\dispaystyle”): {\displaystyle \dispaystyle q(t)=q_0 cos\omega_0 t} gdzie: Parser nie mógł rozpoznać (nieznana funkcja „\dispaystyle”): {\displaystyle \dispaystyle \omega_0=\sqrt{\displaystyle \frac{1}{LC}}} - częstość drgań swobodnych, ${\omega }_{0}t$ - faza drgań, $q_0$ - amplituda drgań. Mając funkcję $q(t)$ można obliczyć napięcie na kondensatorze $U_C(t)$, natężenie prądu $I(t)$ oraz napięcie na zwojnicy $U_L(t)$: $\begin{array}{cc}{U}_C(t)=\frac{q(t)}{C}=\frac{q_0}{C}cos{\omega }_{0}t=(U_C{)}_{0}cos{\omega }_{0}t& (U_C{)}_0=\frac{q_0}{C}\end{array}$ $\begin{array}{cc}I(t)=\frac{dq}{dt}=I_{0}cos({\omega }_{0}t+\pi /2)& I_0=q_0{\omega }_0\end{array}$ $\begin{array}{cc}{U}_L(t)=L\frac{dI}{dt}=(U_L{)}_{0}cos({\omega }_{0}t+\pi )& (U_L{)}_0=\frac{q_0}{C}\end{array}$ Warto zauważyć, że napięcia na kondensatorze i zwojnicy mają równe amplitudy i przeciwne fazy (przesunięcie fazowe wynosi $-\pi$), zaś natężenie prądu jest przesunięte w fazie o $-\pi /2$. Z powyższej analizy wynika, że po dostarczeniu do obwodu LC porcji energii (naładowanie kondensatora) i braku dalszej ingerencji zewnętrznej, zachodzą w nim drgania harmoniczne swobodne - wielkości opisujące stan układu są funkcjami harmonicznymi. Porównanie z mechanicznym oscylatorem harmonicznym swobodnym (np. klocek o masie m zaczepiony do sprężyny o współczynniku sprężystości k) pokazuje, że ładunek na kondensatorze jest wielkością analogiczną do wychylenia z położenia równowagi a natężenie prądu do prędkości. Pełne zestawienie analogii między drganiami elektromagnetycznymi i drganiami mechanicznymi przedstawiono w tabeli nr 14.1. Okres i częstotliwość drgań swobodnych (inaczej drgań własnych) obwodu LC są równe: Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle \displaystyle T_0=\frac{2\pi}{\omeha_0}=2\pi \sqrt{LC}} ${\nu }_0=\frac{1}{T_0}=\frac{1}{2\pi }\sqrt{\frac{1}{LC}}$ Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc $P_E$ i energię $W_E$ pola elektrycznego w kondensatorze $P_E=\frac{W_E}{dt}=U_{C}I=\frac{q}{C}\cdot I$ $W_E=\int \frac{q}{C}dq=\frac{1}{2C}\cdot q^2=\frac{1}{2C}\cdot q_0^{2}co{s}^2{\omega }_{0}t$ oraz moc $P_B$ i energię $W_B$ pola magnetycznego w zwojnicy $P_B=\frac{W_B}{dt}=U_{L}I=L\frac{dI}{dt}\cdot I$ $W_B=\int LIdI=\frac{1}{2}L{I}^2=\frac{1}{2C}\cdot q_0^{2}si{n}^2{\omega }_{0}t$ Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <mathpi/2\,</math>. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy $W=W_A+W_B=\frac{1}{2C}\cdot q^2+\frac{1}{2}L\cdot I^2=\frac{1}{2C}\cdot q_0^2=const.$ jest stała i równa energii dostarczonej do obwodu. Z powyższych rozważań wynika, że elektromagnetyczne drgania swobodne w obwodzie LC można traktować jak okresowe przemiany energii pola elektrycznego w kondensatorze w energię pola magnetycznego w zwojnicy i na odwrót. Okres tych przemian jest równy połowie okresu drgań własnych czyli okresu zmienności napięć na kondensatorze i zwojnicy oraz natężenia prądu. W rzeczywistych obwodach elektrycznych występuje zawsze niezerowy opór elektryczny, a więc wydziela się energia cieplna. W takim przypadku energia układu drgającego maleje i po pewnym czasie drgania zanikają.

---

14.5 Elektromagnetyczne drgania tłumione Drgania harmoniczne tłumione mogą zachodzić w obwodach elektrycznych zawierających elementy $R,L,C$. Załóżmy, że naładowany kondensator o pojemności $C$ zaczyna się rozładowywać przez opór $R$ i zwojnicę o indukcyjności $L$. Zgodnie z drugim prawem Kirchoffa suma zmian potencjału na drodze zamkniętej jest równa zeru $RI+L\frac{dI}{dt}+\frac{q}{C}=0$ Po podstawieniu i podzieleniu stronami przez L otrzymamy równanie $\frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=0$ Jest to równanie elektromagnetycznego oscylatora harmonicznego tłumionego, w którym $\frac{1}{LC}={\omega }_0^2$ oraz $\frac{R}{2L}=\beta$ Gdy spełniony jest warunek $\beta <{\omega }_0$ to rozwiązaniem tego równania różniczkowego jest funkcja “okresowa” $q(t)=q_0{e}^{-\beta t}cos{\omega }_{t}t$ ${\omega }_t=\sqrt{{\omega }_0^2-{\beta }^2}$ zatem ładunek elektryczny w kondensatorze wykonywać będzie drgania tłumione. Na rysunku przedstawiono porównanie drgań swobodnych i tłumionych, dla kilku wartości współczynnika tłumienia. Warto zauważyć, że szybkość zaniku amplitudy drgań silnie zależy od współczynnika tłumienia $\beta$. Natomiast istotny wpływ na częstość drgań tłumionych pojawia się dopiero dla wartości współczynnika tłumienia $\beta$ bliskich wartości granicznej, czyli ${\omega }_0$. Podstawowe różnice między drganiami tłumionymi i drganiami swobdnymi: amplituda drgań maleje eksponencjalnie z upływem czasu, częstość drgań tłumionych jest mniejsza od częstości drgań swobodnych, całkowita energia oscylatora maleje z upływem czasu Gdy spełniony jest warunek $\beta \ge {\omega }_0$ rozwiązaniem równania różniczkowego jest funkcja aperiodyczna. Rozładowanie kondensatora jest eksponencjalne i jednorazowe.

---

14.6 Elektromagnetyczne drgania wymuszone Elektromagnetyczne drgania wymuszone można zaobserować w obwodzie RLC (zawierającym zwojnicę o indukcyjności $L$, kondensator o pojemności $C$ oraz opornik o oporności $R$) do którego dołączone zostało źródło napięcia sinusoidalnego. Stan fizyczny tego układu opisuje w dowolnej chwili II prawo Kirchhoffa: $L\frac{dI}{dt}+RI+\frac{q}{C}=U_{0}sin\omega t$ Po podzieleniu równania przez $L$ i podstawieniu $\begin{array}{ccc}\frac{dq}{dt}=I& \frac{R}{2L}=\beta & \frac{1}{LC}={\omega }_0^2\end{array}$ gdzie: $\beta$ - współczynnik tłumienia, ${\omega }_0$ - częstość drgań swobodnych, otrzymujemy równanie elektromagnetycznych drgań wymuszonych $\frac{d^{2}q}{d{t}^2}+2\beta \frac{dq}{dt}+{\omega }_0^2=\frac{U_0}{L}sin\omega t$ W równaniu tym bezpośrednie parametry układu fizycznego jakimi są w przypadku obwodu RLC: indukcyjność $L$, pojemność $C$ i oporność $R$ zostały zastąpione przez uniwersalne parametry występujące w opisie drgań harmonicznych dowolnego układu fizycznego (np. oscylator harmoniczny mechaniczny), a mianowicie przez częstość drgań własnych ${\omega }_0$ i współczynnik tłumienia $\beta$. Ponieważ napięcie wymuszające jest sinusoidalną funkcją czasu, to rozwiązania tego równania poszukujemy w postaci funkcji $q(t)=q_{0}sin(\omega t-\phi )$ a zatem przewidujemy, że ładunek na kondensatorze będzie się zmieniać sinusoidalnie z częstością taką jak częstość napięcia wymuszającego oraz, że będzie przesunięty w fazie o $\phi$ względem tego napięcia. Po podstawieniu przewidywanej funkcji $q(t)$ do równania i zażądaniu aby równanie to stało się tożsamością (funkcja $q(t)$ musi spełniać to równanie w każdej chwili czasu) otrzymamy wzory określające amplitudę ładunku $q_0$ i przesunięcie fazowe $\phi$ : $q_0=\frac{U_0/L}{\sqrt{({\omega }_0^2-{\omega }^2{)}^2}+4{\beta }^2{\omega }^2}$ $\phi =arctg\frac{2\beta \omega }{{\omega }_0^2-{\omega }^2}$ Przy ustalonych parametrach układu $R,L,C$ (a więc również ${\omega }_0$ i $\beta$) amplituda ładunku oraz przesunięcie fazowe są funkcjami częstości  napięcia wymuszającego. Po przeprowadzeniu badania funkcji $q_0(\omega )$ można stwierdzić, że amplituda ładunku na kondensatorze osiąga wartość maksymalną dla częstości wymuszania ${\omega }_r$ określonej wzorem ${\omega }_r=\sqrt{{\omega }_0^2-2{\beta }^2}$ gdy spełniony jest warunek $\beta <{\omega }_0\frac{\sqrt{2}}{2}={\beta }_g$ Zjawisko wymuszania drgań z taką częstością przy której amplituda drgań osiąga wartość maksymalną nazywamy rezonansem. Rezonans w obwodzie RLC zachodzi przy częstości wymuszania ${\omega }_r$ zwanej częstością rezonansową, gdy współczynnik tłumienia $\beta$ jest mniejszy od wartości granicznej ${\beta }_g$. Gdy tłumienie jest większe $(\beta >{\beta }_g)$ układu RLC nie udaje się wprowadzić w stan rezonansu. Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami: $(q_0{)}_{max}=\frac{U_0/L}{2\beta \sqrt{{\omega }_0^2-{\beta }^2}}$ ${\phi }_r=arctg\frac{\sqrt{{\omega }_0^2-{\beta }^2}}{\beta }$ Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia $\beta =0$. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych ${\omega }_r={\omega }_0$ i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym ${\omega }_r=\pi /2$. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną. Graniczne wartości amplitudy drgań $q_0$ i przesunięcia fazowego  dla częstości wymuszania dążącej do zera wynoszą: $\begin{array}{cc}\underset{\omega \to 0}{\lim }{q}_0=U_{0}C& \underset{\omega \to 0}{\lim }\phi =0\end{array}$ Dla częstości znacznie przekraczających częstość własną, wartości graniczne amplitudy drgań i przesunięcia fazowego wynoszą: $\begin{array}{cc}\underset{\omega \to \mathrm{\infty }}{\lim }{q}_0=0& \underset{\omega \to \mathrm{\infty }}{\lim }\phi =0\end{array}$ 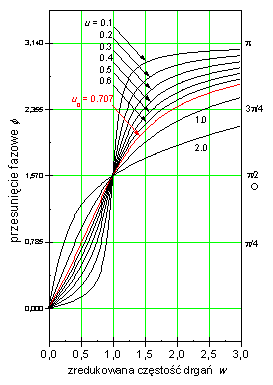Warto jeszcze zaznaczyć, że niezależnie od wartości współczynnika tłumienia, przesunięcie fazowe $\phi$ osiąga wartość $\pi /2$ przy częstości wymuszania $\omega$ równej częstości drgań własnych układu ${\omega }_0$. Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. parametry zredukowane: zredukowany współczynnik tłumienia $u=\frac{\beta }{{\omega }_0}$ zredukowana częstość drgań $w=\frac{\omega }{{\omega }_0}$ zredukowana amplituda drgań wymuszonych $X=\frac{q_0(\omega )}{q_0(\omega \to 0)}=\frac{q_0(\omega )}{U_{0}C}$ Po zastosowaniu powyższych podstawień wzory określające: amplitudę drgań i przesunięcie fazowe dla dowolnej częstości wymuszania, częstość rezonansową oraz amplitudę drgań i przesunięcie fazowe w stanie rezonansu przyjmą postać: $\begin{array}{cc}X=\frac{1}{\sqrt{(1-w^2{)}^2}+4u^2{w}^2}& \phi =arctg\frac{2uw}{1-w^2}\end{array}$ $w_r=\sqrt{1-2u^2}$ $\begin{array}{cc}{X}_r=X(w_r)=\frac{1}{2u\sqrt{1-2u^2}}& {\phi }_r=\phi (w_r)=arctg\frac{\sqrt{1-2u^2}}{u}\end{array}$ 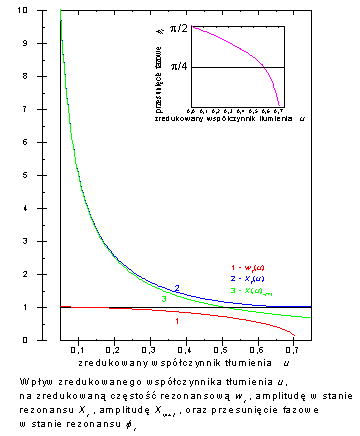Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań $X$ od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia $u$. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa $X(w)$ nie posiada maksimum).

---

---

---

---

---

---

---

---