Zaawansowane algorytmy i struktury danych/Ćwiczenia 7
Zadanie 1
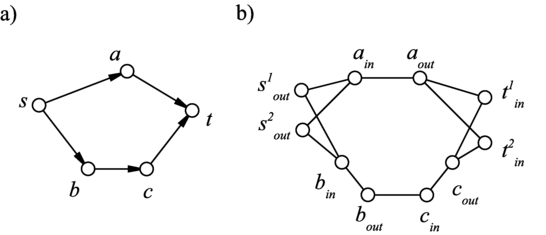
Masz dany graf wraz z dwoma wybranymi wierzchołkami . Pokaż jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalną liczbę wierzchołkowo rozłącznych ścieżek z do . Wierzchołki i będą oczywiście wspólne dla tych ścieżek.
Zadanie 2
Masz daną sieć przepływową wraz z dwoma wybranymi wierzchołkami , w której wszystkie przepustowości krawędzi wynoszą 1. Pokaż jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalny przepływ z do w sieci .
Zadanie 3
Masz daną planarną sieć przepływową wraz z dwoma wybranymi wierzchołkami , w której wszystkie przepustowości krawędzi wynoszą . Pokaż jak rozwiązać problem wyznaczenia maksymalnego przepływu w sieci poprzez znalezienie maksymalnego skojarzenia w planarnym grafie dwudzielnym, tzn., pokaż konstrukcje tak ta przedstawiona w Zadaniu 1 i 2, ale zachowującą planarność grafu.
Zadanie 4
Masz dany graf dwudzielny. Pokaż jak używając algorytmu Hopcrofta-Karpa wyznaczyć minimalne pokrycie wierzchołkowe tego grafu.
Zadanie 5
Niech będzie grafem dwudzielnym. O krawędzi mówimy, że jest dozwolona w jeżeli istnieje doskonałe skojarzenie zawierające . Dwudzielny graf nazywamy natomiast elementarnym jeżeli wszystkie krawędzie są dozwolone. Zaproponuj jak wykorzystując algorytm Hopcrofta-Karpa sprawdzić, czy jest elementarny?