Sr-6-wyk-2.0-Slajd11
Algorytm przecięcia (1)
Algorytm przecięcia (ang. intersection algorithm ) jest zmodyfikowaną wersją algorytmu Marzullo. Celem tego algorytmu jest znalezienie największego pojedynczego przecięcia przedziałów, które będzie zawierało czas mierzony przez zegary o określonej dokładności (ang. truechimer ). Podobnie jak w przypadku algorytmu Marzullo, mamy danych m przedziałów w postaci [ t-d , t+d ].
Główna różnica pomiędzy algorytmem Marzullo, a jego modyfikacją jest fakt, iż wynik uzyskiwany w przypadku tego pierwszego niekoniecznie zawiera środek sumy wszystkich przedziałów. W wypadku algorytmu przecięcia przedział wynikowy zawiera: przedział, który daje w wyniku algorytm Marzullo, a poza tym wspomniany wcześniej środek sumy przedziałów. Taki przedział jest większy, od tego uzyskanego poprzednią wersją algorytmu. To z kolei pozwala na zastosowanie pewnych danych statystycznych w celu wybrania punktu wynikowego z tego przedziału.
Algorytm szuka przedziału, który pokrywałby się z przedziałami m-f źródeł czasu, gdzie f jest liczbą źródeł z wartością czasu poza przedziałem ufności (błędne źródła). Aby otrzymać najlepszy wynik, zakłada się, że f powinno być tak małe jak to tylko możliwe, a wynik jest sensowny gdy f < m/2 (liczba błędnych źródeł nie powinna stanowić więcej niż połowę liczby wszystkich źródeł).
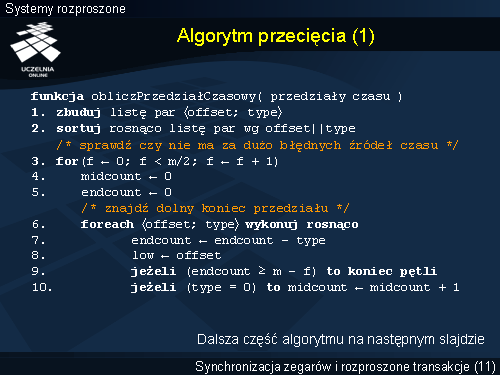
W porównaniu z algorytmem Marzullo w przypadku tego algorytmu każdy przedział jest reprezentowany przez trzy pary: początek przedziału <t-d; -1>, środek przedziału <t; 0> oraz koniec przedziału <t+d; +1>.
Oprócz wcześniej wspomnianych struktur danych, algorytm używa zmiennych: endcount – bieżąca liczba końców przedziałów, midcount – bieżąca liczba środków przedziałów, low – wartość dolnego końca przedziału wynikowego, high – wartość górnego końca przedziału.
Jak wspomniano działanie algorytmu polega na próbie znalezienia przedziału spójnego z m-f źródłami czasu. Przed rozpoczęciem głównej części algorytmu jest tworzona posortowana lista wszystkich dostępnych par, które reprezentują dostępne przedziały czasowe. Sortowanie odbywa się analogicznie jak w algorytmie Murzallo. Algorytm wykonuję się w pętli z rosnącą wartością f . Na początku zakłada się, że nie ma błędnych źródeł czasu, czyli f = 0 . Pętla wykonuje się do momentu kiedy zostanie znaleziony zadowalający przedział lub wartość f będzie równa bądź większa od m/2 . Wewnątrz głównej pętli wykonywane są dwie mniejsze pętle, z których jedna szuka dolnego końca przedziału wynikowego, a druga górnego końca przedziału wynikowego. W skrócie można napisać, iż jedna pętla przegląda na liście pary <znacznik czasowy, typ> w kolejności rosnącej, a druga pętla robi to w kolejności malejącej. Każda z pętli kończy się w momencie, gdy liczba rozpatrzonych przez nie przedziałów mających wspólną część będzie równa lub większa od wartość m-f . Pod koniec obu pętli sprawdzane jest czy liczba środków przedziałów znajdujących się poza przedziałem wynikowym nie przekracza liczby f błędnych źródeł czasu. Jeżeli nie przekracza główna pętla jest kończona i otrzymujemy odpowiedni wynik.