TC Moduł 5
Z Studia Informatyczne

|
Redukcja argumentów |
|
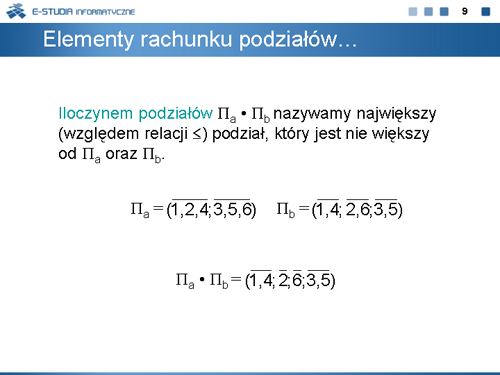
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|

|
|

|
|

|

|

|

|

|

|

|

|

|
Redukcja argumentów |

|
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|

|

|

|

|

|

|

|

|

|

|

|

|