Zpo-4-wyk-Slajd47

Ciąg główny

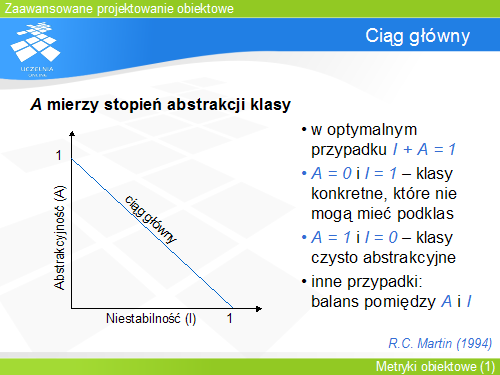
Powiązanie tych dwóch metryk, I i A, pozwoliło Martinowi sformułować tezę o istnieniu tzw. ciągu głównego. Doszedł on do wniosku, że w optymalnym wypadku niestabilność klasy jest kompensowana jej abstrakcyjnością, a więc zachodzi równanie I + A = 1. Jeżeli na układzie współrzędnych osiami będą wartości I i A, wówczas połączenie punktów o współrzędnych (0, 1) i (1, 0) pozwoli narysować odcinek – ciąg główny, który zawiera punkty spełniające podaną zależność.

Dobrze zaprojektowane klasy powinny grupować się na tym wykresie wokół punktów skrajnych, tzn. spełniających równanie oraz bardzo niestabilnych lub bardzo odpowiedzialnych.

<< Poprzedni slajd | Spis treści | Następny slajd >>