CWGI Moduł 3

Elementy równoległe i prostopadłe

---

Dwie proste są do siebie równoległe, jeżeli ich jednoimienne rzuty są równoległe. Własności równoległości prostych w rzutach prostokątnych przedstawiono na rys. 3.1_1a. Zagadnienie to wydaje się oczywiste, wynika, bowiem z niezmienników rzutu równoległego.

---

Prosta jest równoległa do płaszczyzny, jeżeli jest równoległa do dowolnej prostej leżącej w tej płaszczyźnie. W konstrukcjach bezśladowych równoległość ta wydaje się oczywista i sprowadza się do równoległości dwóch prostych, którą opisano wcześniej. Przykład równoległości prostej do płaszczyzny trójkąta przedstawiono na rys. 3.2_1a. Prosta a jest równoległa do płaszczyzny trójkąta, ponieważ jest równoległa do boku Parser nie mógł rozpoznać (błąd składni): {\displaystyle AB \ \Delta (ABC) (a" || AB" oraz\ a' || AB')} .

---

Bardziej złożona jest konstrukcja równoległości prostej do płaszczyzny w przypadku, gdy płaszczyzna określona jest śladami (rys. 3.2_2a). Wynika to z konieczności wyznaczenia w pierwszej kolejności prostej $a$ leżącej w płaszczyźnie. Przypomnijmy tu warunek przynależności prostej do płaszczyzny (ślady prostej muszą leżeć na śladach płaszczyzny). Po wyznaczeniu rzutów prostej a leżącej w płaszczyźnie $\alpha$bez trudu można wyznaczyć rzuty prostej $b||\alpha$ Rzut pionowy prostej $b^{″}$ będzie równoległy do rzutu pionowego prostej $a^{″}$, natomiast rzut poziomy prostej $b^{\prime }$ będzie równoległy do rzutu poziomego prostej $a^{″}$ jeżącej w płaszczyźnie $\alpha$.

---

Równoległość płaszczyzn w rzutach prostokątnych można zdefiniować w sposób następujący:, jeżeli dwie przecinające się proste są równoległe do dwóch innych, przecinających się prostych, to płaszczyzny, jakie tworzą te proste są do siebie równoległe. Można to przedstawić na rys. 3.3_1a. Jedna z płaszczyzn jest określona przez dwie proste przecinające się, druga również, lecz w postaci trójkąta. Płaszczyzna określona przy pomocy dwóch prostych $(axb)$ przecinających się w punkcie $Q$ jest równoległa do płaszczyzny $\mathrm{\Delta }(ABC)$, ponieważ rzuty prostych $aib$ są odpowiednio równoległe do rzutów boków Parser nie mógł rozpoznać (błąd składni): {\displaystyle AC\ i CB\\Delta (ABC)} .

---

W konstrukcjach śladowych warunkiem równoległości płaszczyzn jest równoległość ich jednoimiennych śladów, przecinających się w punkcie właściwym na osi x. To oznacza, że aby dwie płaszczyzny były do siebie równoległe to ich ślady pionowe muszą być do siebie równoległe oraz ślady poziome również muszą być do siebie równoległe. Własność ta jest zgodna z poprzednią, ponieważ ślady płaszczyzny to nic innego jak rzuty dwóch wzajemnie przecinających się prostych, spełniających jedynie warunek położenia na rzutniach (patrz: definicja śladów płaszczyzn) Zwróćmy tu jednak uwagę na fakt, iż ogólnie nie można stwierdzić, że płaszczyzny, których ślady są odpowiednio równoległe, są do siebie równoległe. Przykładem mogą tu być dwie płaszczyzny równoległe do osi x. Ich ślady są do siebie równoległe, lecz płaszczyzny wcale nie muszą być równoległe. Istotnym, zatem jest tu drugi warunek, aby ślady przecinały się na osi x.

---

Ogólnie, jeżeli dwie proste są do siebie prostopadłe, to w rzutach prostokątnych ich rzuty, zwykle, nie są prostopadłe. Są jednak przypadki szczególne, dla których prostopadłość wybranych rzutów jest zachowana. Wynika to oczywiście z niezmienników rzutowania równoległego. Można nawet powiedzieć, iż dodatkowy 9 niezmiennik dotyczy właśnie prostopadłości prostych w rzutach prostokątnych. Niezmiennik ten można sformułować w sposób następujący: kąt prosty, którego jedno z ramion jest równoległe do rzutni, a drugie nie jest prostopadłe do rzutni, zachowuje swą prostopadłość po dokonaniu rzutowania na tą właśnie rzutnię. Można zatem wykorzystać w konstrukcjach prostopadłości dwóch prostych, charakterystyczne położenie prostych szczególnych, tzn. prostej poziomej lub czołowej. Proste równoległe do rzutni to odpowiednio: pozioma (równoległą do rzutni poziomej) oraz czołowa (równoległa do rzutni pionowej). Jeżeli zatem jedno z ramion kąta prostego jest prostą poziomą lub czołową, to rzutem, odpowiednio poziomym dla prostej poziomej i pionowym dla prostej czołowej tego kąta, będą kąty proste. Przedstawiono to na rys. 3.4_1a,b. Rysunek a) przedstawia proste prostopadłe przecinające się, natomiast rys. b) proste prostopadłe skośne względem siebie, gdzie jedno z ramion kąta jest prostą poziomą.

---

Podobna konstrukcja oparta jest na prostej czołowej, a więc równoległej do rzutni pionowej. W tym przypadku prostopadłość będzie zachowana dla rzutów pionowych prostych, przy czym rzuty poziome pozostają w położeniu dowolnym. Rzuty prostokątne prostych prostopadłych a i c przedstawiono na rys. 3.4_2a,b i dotyczą również prostych przecinających się(a) i skośnych (b).

---

Prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dwóch przecinających się prostych leżących w tej płaszczyźnie. Prostopadłość prostej do płaszczyzny ustalana jest w rzutach prostokątnych poprzez konstrukcję prostopadłości dwu prostych. Rzuty prostej prostopadłej do danej płaszczyzny powinny być, zatem prostopadłe odpowiednio do rzutu poziomego prostej poziomej leżącej w płaszczyźnie oraz do rzutu pionowego prostej czołowej leżącej w płaszczyźnie. Aby zatem poprowadzić prostą prostopadłą do płaszczyzny określonej bezśladowo należy wyznaczyć dwie przecinające się proste (poziomą i czołową) leżące w tej płaszczyźnie. Umożliwi to nam wyznaczenie prostej, która będzie prostopadła do jednej i drugiej prostej. Oczywiście, w sensie ogólnym, prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dowolnych przecinających się prostych leżących w płaszczyźnie, jednak konstrukcję taką można zrealizować w rzutowaniu prostokątnym tylko wtedy, jeżeli oprzemy się na prostych szczególnych, ponieważ ich pojedyncze ramiona są równoległe do rzutni. Zamiast wyznaczać proste szczególne leżące w płaszczyźnie, możemy samą płaszczyznę przedstawić przy pomocy dwóch przecinających się prostych - poziomej i czołowej. Na rys. 3.5_1a przedstawiono konstrukcję płaszczyzny <math\alpha(p x c)</math> określonej przy pomocy dwóch prostych: poziomej i czołowej przecinających się w punkcie $1$. Prosta $n$ jest prostopadła do płaszczyzny $\alpha$ponieważ jej rzuty są odpowiednio prostopadłe do rzutu pionowego prostej czołowej i rzutu poziomego prostej czołowej. W przypadku płaszczyzny określonej śladami konstrukcja prostej prostopadłej do płaszczyzny jest znacznie łatwiejsza, ponieważ rzuty prostej powinny być prostopadłe do odpowiednich śladów płaszczyzny (rys. 3.5_1b). Nie kłóci się to z poprzednimi ustaleniami, albowiem ślady płaszczyzny są szczególnie położonymi prostymi: poziomą i czołową, które leżą w płaszczyźnie i jednocześnie leżą na rzutniach. Ślady te oczywiście są prostymi, które przecinają się na osi $x$, spełniają, więc wszystkie warunki do realizacji konstrukcji prostopadłości prostej do płaszczyzny. Na rys. 3.5_1b przedstawiono konstrukcję prostej n prostopadłej do płaszczyzny  określonej śladami. Prosta prostopadła do płaszczyzny przechodzi przez z góry określony punkt $Q$ w przestrzeni. Jak widać rzut pionowy prostej prostopadłej do płaszczyzny ${\displaystyle }$ jest prostopadły do śladu pionowego płaszczyzny $v_{\alpha }$ (ślad pionowy płaszczyzny jest rzutem prostej czołowej leżącej w płaszczyźnie i leżącej na rzutni pionowej), natomiast rzut poziomy prostej prostopadłej $n^{\prime }$ jest prostopadły do śladu poziomego $h_{\alpha }$ (ślad poziomy płaszczyzny jest rzutem prostej poziomej leżącej w płaszczyźnie i leżącej na rzutni poziomej).

---

Dwie płaszczyzny są do siebie prostopadłe, jeżeli jedna z nich zawiera prostą prostopadłą do drugiej płaszczyzny. Można, zatem stwierdzić, że każda płaszczyzna przechodząca przez prostą prostopadłą do płaszczyzny jest do niej prostopadła. A więc przez prostą prostopadłą do płaszczyzny można poprowadzić cały pęk płaszczyzn, które będą prostopadłe do danej płaszczyzny. Na rys.3.6_1a,b przedstawiono płaszczyzny prostopadłe do z góry zadanych płaszczyzn. Na rys. 3.6_1a dana jest płaszczyzna określona za pomocą dwóch przecinających się w punkcie 1 prostych $pic$. Druga płaszczyzna prostopadła do pierwszej określona została za pomocą również dwóch prostych m i n przecinających się w punkcie $Q$, przy czym jedna z nich jest prostopadła do płaszczyzny utworzonej przez proste $pic$. Wynika to z faktu, iż proste $pic$ są odpowiednio równoległe do rzutni poziomej (prosta pozioma p) i rzutni pionowej (prosta czołowa c), a więc prosta $n$ będzie prostopadła do płaszczyzny utworzonej przez te proste, jeżeli rzut pionowy prostej $n^{″}$ będzie prostopadły do rzutu pionowego prostej czołowej $c^{″}$, a rzut poziomy prostej $n^{\prime }$ będzie prostopadły do rzutu poziomego prostej poziomej $p^{\prime }$. W przypadku konstrukcji śladowych (rys. 3.6_1b) w dowolnej płaszczyźnie $\alpha$określonej śladami Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_\alpha i h_\alpha} obieramy dowolną prostą a leżącą w płaszczyźnie, a więc jej ślady Va i abędą leżały na śladach płaszczyzny. W ten sposób skonstruowane rzuty prostej $a$ leżącej w płaszczyźnie $\alpha$ powinny być prostopadłe do odpowiednich śladów płaszczyzny $\beta$. Zatem możemy stwierdzić, że płaszczyzna $\beta$ jest prostopadła do $\alpha$, ponieważ jest prostopadła do prostej $a$, która leży w płaszczyźnie $\alpha$.

---

Zmiana układu odniesienia w geometrii odwzorowań przestrzennych nazwana została transformacją. W celu dokonania transformacji punktu obieramy płaszczyznę Parser nie mógł rozpoznać (błąd składni): {\displaystyle \pi_3} , która jest prostopadła np. do rzutni poziomej, a następnie dokonujemy rzutowania prostokątnego na tą właśnie rzutnię. Na rys. 2.8a przykład ten zilustrowano w rzucie aksonometrycznym. Jak widać poza dwoma rzutami: pionowym i poziomym otrzymaliśmy trzeci rzut punktu oznaczany przez $P^{‴}$. Trzecią rzutnię obracamy następnie dookoła osi transformacji, czyli krawędzi przecięcia się trzeciej rzutni z rzutnią poziomą, do położenia pokrywającego się z rzutnią poziomą. Przenosząc to rozważanie do układu rzutów prostokątnych, w celu wyznaczenia trzeciego rzutu punktu po dokonaniu transformacji układu odniesienia należy postępować w sposób następujący: 1. obrać w sposób dowolny oś transformacji (ślad, krawędź przecięcia się nowej rzutni $p{i}_3$ z rzutnią poziomą). Oś transformacji oznaczać będziemy $x_{1/3}$ , 2. trzeci rzut punktu będzie leżał na odnoszącej prostopadłej do osi transformacji, co wynika z obrotu trzeciej rzutni $p{i}_3$ do położenia na rzutni poziomej $p{i}_1$ . Odległość, w jakiej będzie się znajdował trzeci rzut punktu $P^{‴}$ od osi $x$ jest równa wysokości punktu $P$, czyli odległości tego punktu od rzutni poziomej. Ta odległość jest oczywiście taka sama jak odległość rzutu pionowego punktu $P^{″}$ od osi Parser nie mógł rozpoznać (błąd składni): {\displaystyle x\'} . 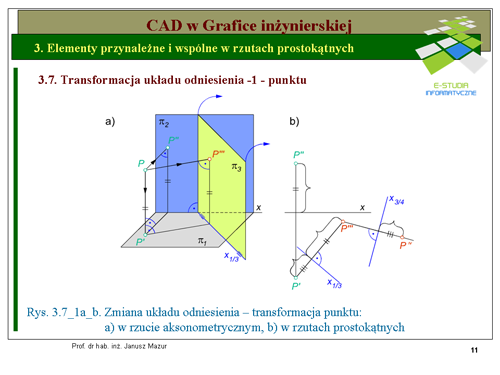Można, zatem stwierdzić, iż odmierzamy od osi $x_{1/3}$ odległość poprzedniego rzutu (P") punktu od poprzedniej osi (x), 3. taką operację możemy powtarzać w miarę potrzeby wielokrotnie, zachowując opisane powyżej zasady. Na rys. 3.7_1a,b przedstawiono dwie kolejne transformacje punktu $P$ w rzucie aksonometrycznym i prostokątnym.

---

Transformacja prostej, to nic innego jak transformacja dwóch punktów należących do niej. Transformację prostej wykonujemy w określonym celu. Zwykle dotyczy to sprowadzania prostej do położenia rzutującego, to znaczy do położenia prostopadłego do rzutni. Takie położenie prostej może być wykorzystywane do rozwiązywania szeregu konstrukcji (np. wyznaczania rzeczywistej odległości dwu prostych skośnych). Sprowadzenie prostej do położenia rzutującego za pomocą transformacji uwarunkowane jest położeniem danej prostej. Położenie prostej równoległe do rzutni umożliwia dokonanie takiej operacji za pomocą jednej transformacji. W tym bowiem przypadku jesteśmy w stanie zaproponować trzecią rzutnię prostopadle do prostej (oś transformacji będzie prostopadła do rzutu poziomego prostej, jeżeli prosta jest równoległa do rzutni poziomej lub prostopadła do rzutu pionowego, jeżeli jest ona równoległa do rzutni pionowej). Na rys.3.7_2a. przedstawiono transformację prostej poziomej (równoległej do rzutni poziomej). Prosta p jest prostą poziomą, więc sprowadzenie jej do położenia rzutującego (do punktu) jest możliwe za pomocą jednej transformacji o osi $x_{1/3}$ prostopadłej do rzutu poziomego prostej. Dokonując transformacji prostej, należy dokonać transformacji dwóch dowolnych punktów należących do niej. Obieramy dwa punkty Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1\ i \2} leżące na prostej, a następnie dokonujemy transformacji tych punktów o osi $x_{1/3}$ . Odmierzając na odnoszącej przechodzącej przez punkty $1^{\prime }i{2}^{\prime }$ i prostopadłej do osi transformacji odległość równą wysokości punktów $1i2$ (odległość Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1" \i\ 2"} od osi $x$) wyznaczymy trzecie rzuty punktów $1^{‴}i{2}^{‴}$, a tym samym i trzeci rzut prostej $p^{‴}$. Sprowadzenie prostej w położeniu dowolnym do położenia rzutującego (do punktu) możliwe jest za pomocą podwójnej transformacji (3.7_2b). W pierwszej sprowadzamy prostą do położenia równoległego z trzecią rzutnią, a następnie za pomocą rzutni czwartej prostopadłej do trzeciego rzutu sprowadzamy ją do położenia rzutującego. W pierwszej transformacji przyjmujemy trzecią rzutnię równolegle do prostej oś transformacji $x_{1/3}$ będzie równoległa do rzutu poziomego prostej $a^{\prime }$). Druga transformacja o osi $x_{3/4}$ będzie prostopadła do trzeciego rzutu. Odmierzając od osi $x_{3/4}$ odległość rzutu poziomego a' od pierwszej osi transformacji otrzymamy czwarte rzuty punktów oraz czwarty rzut prostej $p^{IV}$, który również będzie punktem.

---