GKIW Moduł 4

---

---

Przekształcenia 2D, zapis macierzowy Współczesna grafika komputerowa operuje na milionach elementów (punktów, trójkątów). Przy tak dużej liczbie zachodzi konieczność opisania operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Takie warunki spełnia opis macierzowy. Niech $P={\left[\begin{array}{cc}{x}_p& y_p\\ \end{array}\right]}^T$ opisuje położenie punktu na płaszczyźnie. Najprostszym rozwiązaniem byłoby przyjęcie, że macierz $M(2\times 2)$ opisuje przekształcenie punktu $P$ na $P^{\prime }$ i że $P^{\prime }=M\cdot P$

---

Przekształcenia 2D, obrót, problem przesunięcia I Można zastanowić się nad tym, czy takie podejście do problemu wystarczy do opisu prostych operacji geometrycznych. Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację). Można zaproponować macierz 2x2, która, opisuje obrót punktu wokół początku układu współrzędnych. Analogiczny opis można zaproponować dla operacji skalowania.

---

Przekształcenia 2D, obrót, problem przesunięcia II Niech $M_{T1}=\left[\begin{array}{cc}a& b\\ c& d\\ \end{array}\right]$. Niech wektor $P=\left[\begin{array}{cc}{T}_X& T_Y\\ \end{array}\right]$ opisuje translację punktu na płaszczyźnie. Czy można znaleźć takie a, b, c, d, aby $M_{T1}=\left[\begin{array}{c}{x}_p+T_X\\ y_p+T_Y\\ \end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\\ \end{array}\right]\cdot \left[\begin{array}{c}{x}_p\\ y_p\\ \end{array}\right]$ dla $T_X\ne 0$ i $T_Y\ne 0$ . Widać że nie jest to możliwe dla współrzędnych dowolnego punktu. Na dodatek punkt $P={\left[\begin{array}{cc}0& 0\\ \end{array}\right]}^T$ byłby punktem stałym takiego przekształcenia. 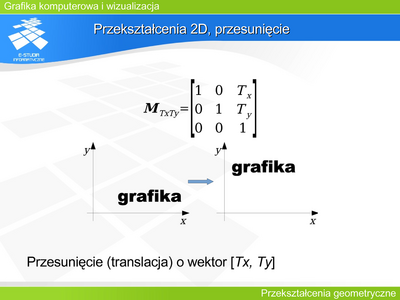Jak zatem opisać translację na płaszczyźnie? 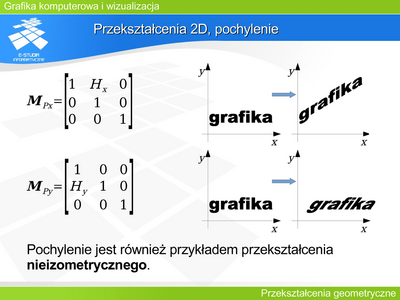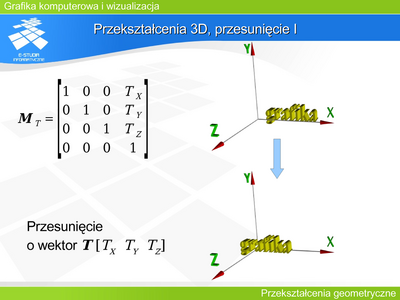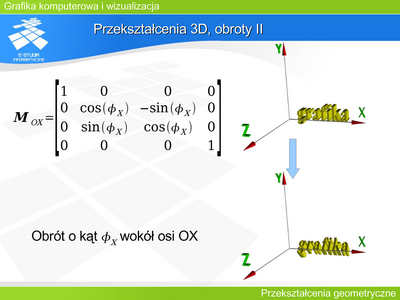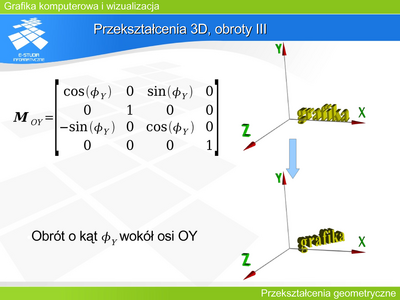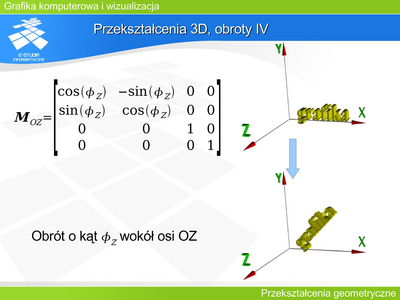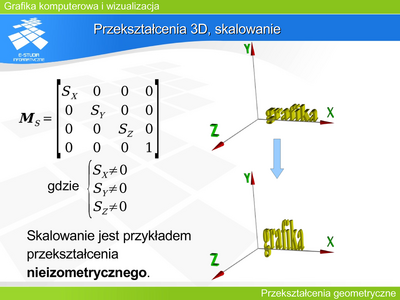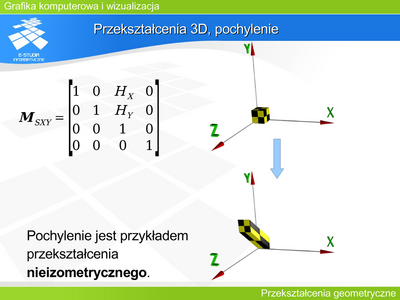Operację tę można opisać macierzą $M=\left[\begin{array}{ccc}1& 0& T_X\\ 0& 1& T_Y\\ 0& 0& 1\end{array}\right]$ Między współrzędnymi zachodzi następujący związek: $M=\left[\begin{array}{c}{X}_p^{\text{'}}\\ Y_p^{\text{'}}\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& T_X\\ 0& 1& T_Y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}{X}_p\\ Y_p\\ 1\end{array}\right]$ i jest to równoważne opisowi translacji o wektor w postaci układu równań: $\{\begin{array}{l}{x}_p^{\text{'}}=x_p+T_X\\ y_p^{\text{'}}=y_p+T_Y\end{array}$ Tak wykonana operacja wymaga użycia współrzędnych jednorodnych.

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---