PEE Moduł 8

Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych

---

Zastosowanie przekształcenia Laplace’a upraszcza operację rozwiązywania równań różniczkowych zastępując ją rozwiązaniem układu równań algebraicznych. Istota przekształcenia Laplace’a polega na tym, że każdej funkcji czasu f(t) określonej dla t>0 odpowiada pewna funkcja F(s) określona w dziedzinie liczb zespolonych i odwrotnie, każdej funkcji F(s) odpowiada określona funkcja czasu f(t). Funkcję f(t) nazywamy oryginałem i oznaczamy małą literą. Funkcję F(s) nazywamy transformatą funkcji określoną w dziedzinie zmiennej zespolonej s i oznaczamy dużą literą. Zmienna s jest nazywana częstotliwością zespoloną, przy czym $s=\sigma +j\omega$, gdzie $\omega$ oznacza pulsację. W elektrotechnice najczęściej używane jest jednostronne przekształcenie Laplace’a, określone parą równań: $F(s)=L\{f(t)\}=\underset{0}{\overset{\mathrm{\infty }}{\int }}f(t)e^{-st}dt$ $f(t)=L^{-1}\{F(s)\}=\frac{1}{2\pi \cdot j}\underset{c-j\omega }{\overset{c+j\omega }{\int }}F(s)e^{st}ds$ w których c jest bliżej nieokreśloną stałą warunkującą położenie granic całkowania w obszarze zbieżności transformaty. Pierwsze z równań definiuje proste przekształcenie Laplace’a przyporządkowujące oryginałowi transformatę zmiennej zespolonej s, a drugie przekształcenie odwrotne dokonujące transformacji odwrotnej, czyli wyznaczające funkcję oryginału na podstawie F(s). Zakładamy przy tym, że funkcja f(t) jest funkcją czasu, zadaną dla t>0 i równą 0 dla t<0 oraz, że nie rośnie szybciej niż funkcja wykładnicza. Proste przekształcenie Laplace’a określone wzorem ze slajdu 2 dokonuje transformacji funkcji czasu f(t) na funkcję F(s) zmiennej zespolonej s. Przekształcenie odwrotne określone wzorem ze slajdu 2 dokonuje transformacji funkcji zespolonej F(s) na funkcję czasu f(t). Wzór ten pełni jedynie rolę definicji i w praktyce nie używa się go do wyznaczania transformaty odwrotnej, wykorzystując w zamian własności transformat Laplace’a.

---

Z wielu istniejących własności przekształcenia Laplace’a ograniczymy się tutaj do kilku podstawowych, których znajomość jest konieczna do określenia stanów nieustalonych w obwodach RLC. Liniowość przekształcenia Jeśli współczynniki $a_1$ i $a_2$ są dowolnymi stałymi to $L[a_1{f}_1(t)+a_2{f}_2(t)]=a_1{F}_1(s)+a_2{F}_2(s)$ $L^{-1}[a_1{F}_1(s)+a_2{F}_2(s)]=a_1{f}_1(t)+a_2{f}_2(t)$ gdzie symbole $L$ i $L^{-1}$ oznaczają odpowiednio transformaty: prostą i odwrotną Laplace’a. Z własności liniowości przekształcenia wynika, że przekształcenie Laplace’a spełnia zasadę superpozycji. Transformata pochodnej funkcji czasu Transformata pochodnej funkcji czasu spełnia relację $L\left[\frac{df(t)}{dt}\right]=sF(s)-f(0^{+})$ W której $f(0^{+})$ oznacza wartość początkową funkcji f(t). Mnożenie funkcji F(s) przez zmienną zespoloną s odpowiada w dziedzinie czasu różniczkowaniu funkcji. Stąd operator s nazywany jest operatorem różniczkowania.

---

Transformata całki funkcji czasu Transformata całki funkcji czasu spełnia relację $L[\underset{0}{\overset{t}{\int }}f(\tau )d\tau ]=\frac{F(s)}{s}$ Pomnożenie funkcji F(s) przez 1/s odpowiada w dziedzinie czasu całkowaniu funkcji. Stąd operator $s^{-1}$ jest nazywany również operatorem całkowania. Transformata splotu Splot stanowi ważne pojęcie w teorii obwodów, gdyż za jego pośrednictwem określa się odpowiedzi czasowe obwodów rzeczywistych RLC. Splot dwu funkcji czasu $f_1(t)$ i $f_2(t)$ oznaczony w postaci $f_1(t)*f_1(t)$ jest zdefiniowany w następujący sposób $f_1(t)*f_1(t)=\underset{0}{\overset{t}{\int }}{f}_1(\tau )f_2(t-\tau )d\tau =\underset{0}{\overset{t}{\int }}{f}_1(t-\tau )f_2(\tau )d\tau$ Transformata Laplace’a splotu jest równa zwykłemu iloczynowi transformat poszczególnych funkcji tworzących splot $L[f_1(t)*f_2(t)]=F_1(s)\cdot F_2(s)$ Powyższa własność nosi w matematyce nazwę twierdzenia Borela. Zauważmy, że mnożenie splotowe dwu funkcji w dziedzinie czasu odpowiada zwykłemu mnożeniu ich transformat w dziedzinie częstotliwości. Własność ta jest szczególnie wygodna w analizie obwodów zarówno w stanie ustalonym jak i nieustalonym. Zamiast żmudnych operacji w dziedzinie czasu wykonuje się transformację Laplace’a funkcji czasowych a następnie wszystkie operacje wykonuje na transformatach.

---

Obliczanie transformat Laplace’a polega na zastosowaniu wzoru ze slajdu 2 przy zadanej funkcji oryginału i przeprowadzeniu działań w nim określonych (całkowanie funkcji i wyznaczenie wartości na granicach całkowania). Obliczanie transformat dla większości funkcji, zwłaszcza bardziej złożonych, nie jest procesem łatwym i dlatego w praktyce inżynierskiej najczęściej posługujemy się tablicami gotowych transformat Laplace’a, których źródło znaleźć można w wielu poradnikach matematycznych jak również podręcznikach poświęconych rachunkowi operatorowemu. W tablicy na slajdzie obok zestawiono wybrane przykłady transformat Laplace’a szczególnie często wykorzystywanych przy rozwiązywaniu stanów nieustalonych w obwodach RLC. W dalszej części tej lekcji będą one wykorzystane do wyznaczania transformat odwrotnych Laplace’a (funkcji czasu odpowiadających transformatom). Zawartość tablicy przedstawiająca zbiór funkcji czasu wraz z odpowiadającymi im transformatami może służyć zarówno wyznaczaniu transformaty Laplace’a przy zadanej funkcji czasu jak i działaniu odwrotnemu, to jest wyznaczeniu oryginału na podstawie zadanej postaci transformaty.

---

Aby wyznaczyć funkcję czasu f(t) na podstawie danej transformaty należy dokonać odwrotnego przekształcenia Laplace’a. Zależność definicyjna określona wzorem na oryginał (slajd 2) jest raczej bezużyteczna ze względu na konieczność całkowania złożonych zwykle funkcji, jak również na nieokreślone precyzyjnie granice całkowania (stała c w definicji nie jest dokładnie określona). Najczęściej korzysta się z pośrednich metod wyznaczania oryginału wynikających z własności samego przekształcenia. Niezależnie od metody zastosowanej do wyznaczenia oryginału, zakładać będziemy, że transformata Laplace’a zadana jest w postaci wymiernej, czyli ilorazu dwu wielomianów zmiennej zespolonej s o współczynnikach rzeczywistych. $F(s)=\frac{L(s)}{M(s)}=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0}$ Dodatkowo przyjmiemy, że stopień licznika jest mniejszy niż stopień mianownika. Jeśli warunek powyższy byłby niespełniony, należy podzielić licznik przez mianownik tak, aby wymusić spełnienie tego warunku Istnieje wiele metod obliczania transformaty odwrotnej Laplace’a, wykorzystujących własności przekształcenia. Do najbardziej popularnych należą metoda residuów, rozkładu funkcji wymiernej na ułamki proste, metoda Heaviside’a oraz metoda bazująca na wykorzystaniu tablic transformat Laplace’a. Tutaj ograniczymy się do dwu najbardziej uniwersalnych metod: metody residuów oraz metody tablicowej wykorzystującej tablice transformat Laplace’a.

---

Załóżmy, że funkcja wymierna F(s) zadana jest w postaci ilorazu dwu wielomianów zmiennej zespolonej s. Pierwiastki licznika funkcji transformaty są nazywane zerami a pierwiastki mianownika biegunami. Zauważmy, że bieguny są utożsamione z pierwiastkami równania charakterystycznego występującego w metodzie klasycznej lub wartościami własnymi macierzy stanu A. W metodzie residuów korzysta się z następującego twierdzenia. Twierdzenie Jeżeli funkcja $F(s)$ jest ilorazem dwu wielomianów $L(s)$ i $M(s)$, przy czym stopień wielomianu mianownika jest wyższy niż stopień wielomianu licznika $(n>m)$ to oryginał funkcji $f(t)$ określony jest następującym wzorem $L^{-1}[F(s)]=\sum _{i=1}^{n}re{s}_{s=s_i}[F(s)e^{st}]$ Sumowanie odbywa się po wszystkich biegunach funkcji operatorowej F(s) niezależnie od tego, czy bieguny są pojedyncze czy wielokrotne. Residuum funkcji $res[o]$ wyznacza się korzystając ze wzorów wynikających z własności przekształcenia Laplace’a.

---

W przypadku bieguna l-krotnego wzór jest następujący $re{s}_{s=s_i}[F(s)e^{st}]=$ $=\frac{1}{(l-1)!}li{m}_{s\to s_i}\frac{d^{(l-1)}}{d{s}^{l-1}}[F(s)(s-s_i{)}^l{e}^{st}]$ Szczególnie proste zależności otrzymuje się dla bieguna jednokrotnego $s_i$ . W takim przypadku l=1 i wzór na residuum ulega znacznemu uproszczeniu $re{s}_{s=s_i}[F(s)e^{st}]=li{m}_{s\to s_i}[F(s)(s-s_i)e^{st}]$ Wzór z poprzedniego slajdu wykorzystujący residuum funkcji jest stosowalny dla dowolnych biegunów funkcji F(s), w tym biegunów rzeczywistych, zespolonych, jednokrotnych i wielokrotnych. Jednakże przy biegunach zespolonych obliczenie residuum jest procesem dość złożonym i metoda nie jest konkurencyjna względem innych.

---

Jako przykład rozpatrzmy wyznaczenie transformaty odwrotnej Laplace’a funkcji F(s) danej wzorem $F(s)=\frac{5s}{(s+1)(s+3)}$ Zadana funkcja ma dwa bieguny: $s_1=-1$ oraz $s_2=-3$ . Wykorzystując wzór ze slajdu 6 otrzymuje się $f(t)=re{s}_{s=s_1}[F(s)e^{st}]+re{s}_{s=s_2}[F(s)e^{st}]$ Na podstawie wzoru na residuum otrzymuje się $f(t)=li{m}_{s\to s_1}[F(s)(s+1)e^{st}]+li{m}_{s\to s_2}[F(s)(s+3)e^{st}]=$ $=\frac{5\cdot (-1)}{(-1+3)}{e}^{-1t}+\frac{5\cdot (-3)}{(-3+1)}{e}^{-3t}=-2,5e^{-t}+7,5e^{-3t}$

---

Metoda residuów jakkolwiek koncepcyjnie bardzo prosta staje się żmudna, jeśli bieguny układu są zespolone. Jest to szczególnie widoczne przy wysokich stopniach mianownika transmitancji operatorowej. W takich przypadkach zwykle korzystniejsze jest zastosowanie metody wykorzystującej tablice transformat Laplace’a. Przy korzystaniu z tablic transformat należy poprzez elementarne przekształcenia doprowadzić daną transformatę do postaci standardowej znajdującej się w tablicy transformat (u nas tablica ze slajdu 4) a następnie odczytać z niej oryginał. Jest ona szczególnie wygodna jeśli bieguny układu są zespolone, gdyż w procesie przekształcania transformaty nie występuje potrzeba wyznaczania tych biegunów a wszystkie obliczenia dokonywane są na wartościach rzeczywistych. W praktyce przy stosowaniu tej metody transmitancję wyższych rzędów (n>2) rozkłada się na składniki rzędu drugiego i wszystkie przekształcenia dokonuje na wielomianach rzędu pierwszego lub drugiego. Idę metody wyjaśnimy na przykładach liczbowych. Przykład Obliczyć transformatę odwrotną Laplace’a dla funkcji F(s) danej w postaci $F(s)=\frac{1}{s^2+s+1}$ Wobec zespolonych pierwiastków mianownika wykorzystamy tablicę transformat ze slajdu 4. Porównanie postaci danej transformaty z danymi zawartymi w tablicy wskazuje, że należy ją doprowadzić do postaci transformaty odpowiadającej funkcji sinusoidalnej tłumionej wykładniczo (wiersz 6 w tablicy). Kolejność czynności jest tu następująca $F(s)=\sqrt{4/3}\frac{\sqrt{3/4}}{(s+0,5{)}^2+(\sqrt{3/4}{)}^2}$ Porównanie tej postaci z wierszem szóstym tablicy ze slajdu 4 pokazuje, że $\alpha =0,5$, a $\omega =\sqrt{3/4}$. Funkcja oryginału jest więc określona wzorem $f(t)=\sqrt{4/3}{e}^{-0,5t}sin(\sqrt{3/4}t)$

---

Modele operatorowe elementów obwodu Aby uzyskać bezpośrednie przetworzenie postaci oryginalnej obwodu na obwód w dziedzinie operatorowej Laplace’a należy każdy element obwodu zastąpić odpowiednim modelem w dziedzinie operatorowej. Tutaj podamy te modele dla trzech podstawowych elementów obwodu RLC. Rezystor Prawo Ohma dotyczące wartości chwilowych prądu i napięcia dla rezystora można zapisać w postaci $u_R(t)=R{i}_R(t)$ Jest to równanie algebraiczne wiążące prąd i napięcie na zaciskach elementu. Stosując transformację Laplace’a do obu stron równania otrzymuje się $U_R(s)=R{I}_R(s)$ Jak wynika z powyższej zależności impedancja operatorowa dla rezystora jest równa samej rezystancji $Z_R(s)=R$. Rysunek pierwszy na slajdzie 10 przedstawia model operatorowy rezystora, obowiązujący w dziedzinie zmiennej zespolonej s. Cewka Dla uzyskania modelu operatorowego cewki idealnej zastosujemy przekształcenie Laplace’a bezpośrednio do równania opisującego cewkę w dziedzinie czasu $u_L(t)=L\frac{d{i}_L(t)}{dt}$ i wykorzystamy własność dotyczącą transformaty pochodnej. W efekcie otrzymuje się $U_L(s)=sL{I}_L(s)-L{i}_L(0^{+})$ Powyższemu równaniu można przyporządkować schemat obwodowy cewki w dziedzinie operatorowej przedstawiony na rysunku drugim na slajdzie 10. Jest to połączenie szeregowe impedancji operatorowej odpowiadającej cewce idealnej i źródła napięciowego. Zaciski A-B modelu odpowiadają zaciskom A-B w oryginalnym symbolu cewki. Impedancja $Z_L(s)=sL$ jest impedancją operatorową cewki a $L{i}_L(0^{+})$ reprezentuje źródło napięcia stanowiące integralną część modelu. Kondensator Dla uzyskania modelu operatorowego kondensatora idealnego skorzystamy z jego opisu w dziedzinie czasu $i_C(t)=C\frac{d{u}_C}{dt}$ Zastosujemy przekształcenie Laplace’a do obu stron równania kondensatora. W efekcie takiej operacji otrzymuje się $I_C(s)=sC{U}_C(s)-C{u}_C(0^{+})$ Przepiszemy tę zależność w postaci $U(s)=\frac{1}{sC}{I}_C(s)+\frac{u_C(0^{+})}{s}$ Równaniu powyższemu można przyporządkować schemat operatorowy kondensatora przedstawiony na rysunku trzecim na slajdzie 10. W modelu tym funkcja $Z_C=\frac{1}{sC}$ reprezentuje impedancję operatorową kondensatora a $\frac{u_C(0^{+})}{s}$ - źródło napięciowe stanowiące integralną część modelu. Modele operatorowe odpowiadające podstawowym elementom obwodu pozwalają przyporządkować każdemu obwodowi rzeczywistemu jego schemat zastępczy w dziedzinie transformat. W schemacie tym niezerowe warunki początkowe uwzględnione są poprzez dodatkowe źródła napięcia występujące w modelu operatorowym cewki i kondensatora. Taki sposób podejścia do analizy stanu nieustalonego jest wygodny ze względu na to, że umożliwia napisanie równań (algebraicznych, funkcyjnych) w postaci operatorowej bezpośrednio na podstawie schematu zastępczego bez potrzeby tworzenia równań różniczkowych opisujących obwód.

---

Prawa Kirchhoffa dla transformat Dla schematu operatorowego obwodu słuszne są prawa Kirchhoffa, analogiczne do praw obowiązujących w dziedzinie czasu. Prawo prądowe Suma transformat prądów w dowolnym węźle obwodu elektrycznego jest równa zeru $\sum _{k=1}^n{I}_k(s)=0$ Prawo napięciowe Suma transformat napięć gałęziowych w dowolnym oczku obwodu elektrycznego jest równa zeru $\sum _{k=1}^n{U}_k(s)=0$ W równaniach tych transformaty prądów i napięć zastąpiły wartości czasowe występujące w podstawowej wersji praw Kirchhoffa. Znaki prądów i napięć występujących w równaniach na transformatę Laplace’a splotu (slajd 3) i równanie na slajdzie 5 ustalane są w identyczny sposób jak w przypadku podstawowej wersji praw Kirchhoffa podanych dla wielkości rzeczywistych.

---

Obliczenia prądów i napięć w stanie nieustalonym obwodu metodą operatorową Obliczenia prądów i napięć w stanie nieustalonym obwodu metodą operatorową sprowadzać się będą do wyznaczenia transformaty odpowiedniej wielkości a następnie obliczenia transformaty odwrotnej Laplace’a dla określenia zmiennej w dziedzinie czasu. Do obliczenia transformat prądów i napięć można stosować wszystkie poznane dotąd metody analizy obwodów, w tym metodę równań Kirchhoffa, oczkową, potencjałów węzłowych, Thevenina i Nortona operujące transformatami Laplace’a zamiast wartościami zespolonymi czy wartościami w dziedzinie czasu (dla obwodu rezystancyjnego). Podstawowymi zaletami metody operatorowej jest łatwość uwzględnienia niezerowych warunków początkowych (przez wprowadzenie źródeł napięciowych w modelu operatorowym) oraz sprowadzenie operacji różniczkowych do działań algebraicznych. W ogólności rozwiązując stan nieustalony w obwodzie metodą operatorową należy wyróżnić kilka etapów. 1. Określenie warunków początkowych w obwodzie, poprzez wyznaczenie rozwiązania ustalonego obwodu przed przełączeniem i obliczenie wartości napięć na kondensatorach i prądów cewek w chwili $t=0^{-}$, to jest $i_L(0^{-})$ oraz $u_C(0^{-})$ 2. Określenie rozwiązania obwodu w stanie ustalonym po przełączeniu przy zastosowaniu metody symbolicznej z wykorzystaniem dowolnej metody analizy. Wynikiem jest postać czasowa rozwiązania ustalonego prądów cewek $i_{Lu}(t)$ i napięć kondensatorów $u_{Cu}(t)$. Przez założenie t=0 otrzymuje się wartości prądów i napięć w chwili początkowej, to jest $i_{Lu}(0^{+})$ oraz $u_{Cu}(0^{+})$. Określenie rozwiązania obwodu w stanie przejściowym po przełączeniu przy zastosowaniu metody operatorowej. 3. Rozwiązanie obwodu w stanie nieustalonym jest sumą składowej ustalonej oraz składowej przejściowej, to jest $i_L(t)=i_{Lu}(t)+i_{Lp}(t)$ $u_C(t)=u_{Cu}(t)+u_{Cp}(t)$ Składowa przejściowa zanika z czasem do zera i pozostaje jedynie składowa ustalona określająca przebieg wielkości w stanie ustalonym. Taka metodyka rozwiązania stanów nieustalonych przy zastosowaniu transformacji Laplace’a nosi nazwę metody superpozycji stanów, gdyż rozdziela w sposób jawny stan ustalony od stanu przejściowego. Jest szczególnie zalecana przy wymuszeniach sinusoidalnych, choć obowiązuje również dla obwodów prądu stałego. Zaletą takiego podejścia jest jej uniwersalność i stosowalność do każdego obwodu liniowego RLC niezależnie od rodzaju wymuszenia (wymuszenia stałe lub sinusoidalne mają jedynie wpływ na stan ustalony i są wyeliminowane przy rozwiązywaniu stanu przejściowego).

---

W celu obliczenia składowej przejściowej w obwodzie należy wykonać następujące etapy: utworzenie schematu obwodu dla składowej przejściowej poprzez wyeliminowanie źródeł zewnętrznych wymuszających (zwarcie źródeł napięcia i rozwarcie źródeł prądu); obwód rzeczywisty dla składowej przejściowej w dziedzinie czasu nie zawiera żadnych źródeł wymuszających określenie warunków początkowych dla składowej przejściowej przy wykorzystaniu praw komutacji, zgodnie z którymi $x(0^{-})=x_u(0^{+})+x_p(0^{+})$; z równania tego wynikają następujące wzory na warunki początkowe dla składowych przejściowych prądu cewki i napięcia kondensatora $i_{Lp}(0^{+})=i_L(0^{-})-i_{Lu}(0^{+})$ $u_{Cp}(0^{+})=u_C(0^{-})-u_{Cu}(0^{+})$ utworzenie schematu operatorowego obwodu w stanie przejściowym poprzez zastąpienie elementów rzeczywistych obwodu ich modelami operatorowymi dla składowej przejściowej i rozwiązanie obwodu względem poszukiwanych prądów i napięć operatorowych wyznaczenie transformaty odwrotnej Laplace’a dla poszukiwanych wielkości przejściowych określonych w punkcie poprzednim; w wyniku otrzymuje się $i_{Lp}(t)$ oraz $u_{Cp}(t)$. Należy podkreślić, że rozbicie stanu nieustalonego na ustalony i przejściowy jest zalecane jedynie przy istnieniu wymuszeń sinusoidalnych w obwodzie po przełączeniu. Jeśli źródła takie nie występują schemat operatorowy może dotyczyć obwodu całkowitego, bez rozbijania go na schemat dla składowej ustalonej i przejściowej. W takim przypadku pozostawia się zewnętrzne źródła wymuszające w obwodzie przyjmując ich model operatorowy, czyli zastępując postać czasową źródła (wartość stała A przy wymuszeniu stałym) przez funkcję $\frac{A}{s}$. Warunki początkowe również nie podlegają modyfikacji, co oznacza, że $i_L(0^{+})=i_L(0^{-})$ oraz $u_C(0^{+})=u_C(0^{-})$.

---

Przykład Określić prąd cewki w stanie nieustalonym po przełączeniu w obwodzie przedstawionym na slajdzie 14. Przyjąć następujące wartości parametrów obwodu: $R=2\mathrm{\Omega }$, $L=1H$, $C=1/4F$. Zakładamy, że przełączanie zapewnia ciągłość prądu cewki podlegającej przełączeniu. Rozwiązanie 1) Warunki początkowe w obwodzie: $\omega =4$ $I_L=\frac{10e^{j45^{\circ }}}{4+j4}=\frac{2,5}{\sqrt{2}}$ $i_L(t)=2,5sin(4t)$ $i_L(0^{-})=0$ $u_C(0^{-})=0$

---

2) Stan ustalony po przełączeniu w obwodzie (slajd 15) $I_{Lu}=\frac{10e^{j45^{\circ }}}{2+j4-j1}=2,77e^{-j11,31^{\circ }}$ $U_{Cu}=-j1\cdot I_{Lu}=2,77e^{-j101,31^{\circ }}$ $i_{Lu}(t)=2,77\sqrt{2}sin(4t-11,31^{\circ })$ $u_{Cu}(t)=2,77\sqrt{2}sin(4t-101,31^{\circ })$ $i_{Lu}(0^{+})=-0,76$ $u_{Cu}(0^{+})=-3,84$

---

3) Stan przejściowy po przełączeniu Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: $i_{Lp}(0^{+})=i_L(0^{-})-i_{Lu}(0^{+})=0,76$ $u_{Cp}(0^{+})=u_C(0^{-})-u_{Cu}(0^{+})=3,84$

---

Postać operatorowa rozwiązania $I_{Lp}(s)=\frac{L{i}_{Lp}(0^{+})-\frac{u_{Cp}(0^{+})}{s}}{s+2+\frac{4}{s}}=\frac{0,76s-3,84}{s^2+2s+4}$ Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią $I_{Lp}(s)=\frac{0,76(s+1)-4,6\cdot \frac{1}{\sqrt{3}}\sqrt{3}}{(s+1{)}^2+(\sqrt{3}{)}^2}$ $i_{Lp}(t)=0,76e^{-t}cos(\sqrt{3}t)-2,67e^{-t}sin(\sqrt{3}t)$ Rozwiązanie całkowite na prąd cewki w stanie nieustalonym $i_L(t)=i_{Lu}(t)+i_{Lp}(t)=$ $=2,77\sqrt{2}sin(4t-11,31^{\circ })+0,76e^{-t}cos(\sqrt{3}t)-2,67e^{-t}sin(\sqrt{3}t)$

---

Stan nieustalony w obwodzie RLC przy załączeniu napięcia stałego Rozwiązanie operatorowe Rozpatrzmy załączenie napięcia stałego E do gałęzi szeregowej RLC przedstawionej na rys. pierwszym na slajdzie 18. Wobec zerowych warunków początkowych (brak wymuszenia w obwodzie przed przełączeniem) mamy $u_C(0^{-})=0$, $i_L(0^{-})=0$. Schemat operatorowy obwodu w stanie nieustalonym przedstawiony jest na rys. drugim na slajdzie 18. Warunki początkowe napięcia kondensatora i prądu cewki określają równania $u_C(0^{+})=u_C(0^{-})=0$ $i_L(0^{+})=i_L(0^{-})=0$

---

Z prawa napięciowego Kirchhoffa zastosowanego do obwodu wynika następująca postać operatorowa prądu cewki $I(s)=\frac{E/s}{sL+R+1/sC}=\frac{E/L}{s^2+\frac{R}{L}s+\frac{1}{LC}}$ Dla wyznaczenia transformaty odwrotnej należy obliczyć pierwiastki mianownika transmitancji, czyli $s^2+\frac{R}{L}s+\frac{1}{LC}=0$ W wyniku rozwiązania tego równania otrzymuje się dwa pierwiastki (bieguny układu) $s_1=-\frac{R}{2L}+\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}$ $s_2=-\frac{R}{2L}-\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}$

---

Z postaci wzoru opisującego bieguny wynika, że w zależności od znaku funkcji podpierwiastkowej możliwe są 3 przypadki rozwiązania. Przypadek aperiodyczny dla $R>2\sqrt{\frac{L}{C}}$. Przy spełnieniu tego warunku oba bieguny są rzeczywiste i ujemne. Charakter zmian prądu w obwodzie w stanie przejściowym jest aperiodyczny (nieokresowy) zanikający do zera w sposób wykładniczy. Przypadek aperiodyczny krytyczny występujący dla $R=2\sqrt{\frac{L}{C}}$. Przy spełnieniu tego warunku oba bieguny są rzeczywiste i równe sobie. Charakter zmian prądu w obwodzie w stanie przejściowym jest również aperiodyczny, podobnie jak w przypadku pierwszym, ale czas dochodzenia do wartości ustalonych (z określona tolerancją) jest najkrótszy z możliwych. Przypadek oscylacyjny (periodyczny) występujący dla $R<2\sqrt{\frac{L}{C}}$. Przy spełnieniu tego warunku oba bieguny są zespolone (zespolony i sprzężony z nim). Charakter zmian prądu w obwodzie w stanie przejściowym jest sinusoidalny tłumiony, o oscylacjach zanikających do zera. Rezystancja $R=2\sqrt{\frac{L}{C}}$ nazywana jest rezystancją krytyczną i oznaczana w postaci $R_{kr}$.

---

Przypadek aperiodyczny Rozpatrzymy najpierw przypadek pierwszy (aperiodyczny). Ze względu na to, że oba bieguny są rzeczywiste w obliczeniach transformaty odwrotnej najwygodniej jest zastosować metodę residuów. Zgodnie z nią przebieg czasowy prądu $i(t)$ można zapisać w postaci $i(t)=\frac{E}{2L\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}}[e^{s_{1}t}-e^{s_{2}t}]=$ $=\frac{E}{L\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}}{e}^{-\frac{R}{2L}t}sh(\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}t)$ We wzorze występuje czynnik tłumiący typu wykładniczego $e^{-\frac{R}{2L}t}$. Wielkość $\alpha =\frac{R}{2L}$ nazywana jest współczynnikiem tłumienia. Jej wartość jest proporcjonalna do wartości rezystancji. Im większa rezystancja tym większe tłumienie w obwodzie. W podobny sposób wyznaczyć można pozostałe przebiegi czasowe w obwodzie: napięcie cewki i kondensatora. $u_C(t)=E+\frac{E}{2\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}}[s_2{e}^{s_{1}t}-s_1{e}^{s_{2}t}]$ $u_L(t)=L\frac{di}{dt}=\frac{E}{2\sqrt{(\frac{R}{2L}{)}^2-\frac{1}{LC}}}[s_1{e}^{s_{1}t}-s_2{e}^{s_{2}t}]$

---

Na slajdzie 22 przedstawiono przebiegi prądu, napięcia na kondensatorze i cewce w stanie nieustalonym w obwodzie RLC dla $R=2,3\mathrm{\Omega }$, $C=1F$, $L=1H$.przy załączeniu napięcia stałego $E=1V$. Dla przyjętych wartości parametrów elementów mamy do czynienia z przypadkiem aperiodycznym. Prąd w obwodzie oraz napięcie na kondensatorze zachowują ciągłość i spełniają prawa komutacji. W stanie ustalonym prąd w obwodzie nie płynie (kondensator w stanie ustalonym stanowi przerwę) a napięcie na kondensatorze przyjmuje wartość napięcia zasilającego E. Zauważmy ponadto, że wartości maksymalnej prądu odpowiada zerowa wartość napięcia na cewce ($u_L(t)=L\frac{di}{dt}$). W chwili, gdy napięcie na cewce osiąga wartość maksymalną ujemną, w przebiegu napięcia na kondensatorze można zauważyć punkt przegięcia.

---

Interesujące jest porównanie procesu ładowania kondensatora w obwodzie RLC w stanie aperiodycznym oraz w obwodzie RC. Napięcie i prąd kondensatora w obwodzie RC, jak zostało pokazane w lekcji jedenastej opisane są funkcjami $u_C(t)=E(1-e^{-\frac{t}{RC}})$, $i_C(t)=\frac{E}{R}{e}^{-\frac{t}{RC}}$. Na slajdzie 23 przedstawiono przebiegi napięcia na kondensatorze oraz prądu. W napięciu $u_C(t)$ w obwodzie RLC widoczny jest łagodnie narastający przebieg z punktem przegięcia. Prąd ładowania kondensatora, będący jednocześnie prądem cewki, narasta od wartości zerowej z zachowaniem ciągłości, a więc spełniając warunki nakładane przez prawa komutacji. W obwodzie RC widoczny jest gwałtowny skok prądu w chwili przełączenia (prawa komutacji nie dotyczą prądu kondensatora).

---

Przypadek aperiodyczny krytyczny W przypadku aperiodycznym krytycznym, wobec spełnienia relacji $R=2\sqrt{\frac{L}{C}}$ oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem $I(t)=\frac{E/L}{(s+\frac{R}{2L}{)}^2}$

---

Zastosowanie wzoru na residuum dla pierwiastka podwójnego $s_1=s_2=-\frac{R}{2L}=-\alpha$ prowadzi do następującej postaci prądu cewki $i(t)$ $i(t)=\frac{E}{L}{e}^{-\frac{R}{2L}t}$ W analogiczny sposób można wyznaczyć pozostałe przebiegi (napięcia kondensatora i cewki) dla stanu aperiodycznego krytycznego. W przypadku napięcia na cewce bezpośrednio poprzez różniczkowanie funkcji czasowej prądu otrzymuje się $u_L(t)=L\frac{di}{dt}=E{e}^{-\frac{R}{2L}t}(1-\frac{R}{2L}t)$ Napięcie na kondensatorze w stanie nieustalonym można uzyskać bezpośrednio z prawa napięciowego Kirchhoffa napisanego dla obwodu z rys. pierwszego na slajdzie 10 po przełączeniu. Mianowicie $u_C(t)=E-R{i}_L(t)-u_L(t)=E-E^{-\frac{R}{2L}t}(1+\frac{R}{2L}t)$

---

Na slajdzie 26 przedstawiono przebieg ładowania kondensatora w stanie aperiodycznym krytycznym na tle przypadku aperiodycznego. Jedyna różnica występuje w czasie trwania stanu przejściowego, który najszybciej zanika dla przypadku krytycznego. Charakter przebiegu prądu i napięć w obwodzie dla przypadku aperiodycznego krytycznego jest podobny do zwykłego przypadku aperiodycznego, z tym, że najszybciej uzyskiwany jest stan ustalony (stan przejściowy trwa najkrócej z możliwych).

---

Przypadek oscylacyjny Jedyna różnica występuje w czasie trwania stanu przejściowego, który najszybciej zanika dla przypadku krytycznego. Charakter przebiegu prądu i napięć w obwodzie dla przypadku aperiodycznego krytycznego jest podobny do zwykłego przypadku aperiodycznego, z tym, że najszybciej uzyskiwany jest stan ustalony (stan przejściowy trwa najkrócej z możliwych). Przypadek oscylacyjny zmian prądu i napięć w obwodzie szeregowym RLC występuje przy spełnieniu warunku $R<2\sqrt{\frac{L}{C}}$ a więc przy małych wartościach rezystancji R. W tym przypadku oba bieguny są zespolone. Dla wyznaczenia postaci czasowej prądu wygodniej jest zastosować metodę tablic transformat. W tym celu należy przekształcić wyrażenie na prąd operatorowy w taki sposób, aby doprowadzić je do postaci występującej w tablicy na slajdzie 4. Dla zadanej postaci prądu przekształcenia te są jak następuje Wprowadźmy oznaczenie $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$ Wielkość $\omega$ jest pulsacją drgań własnych obwodu RLC występujących w przypadku oscylacyjnym.

---

Wykorzystując tablicę transformat 12.1 możemy uzyskać postać czasową prądu w obwodzie. Można ją zapisać w postaci $i(t)=\frac{E}{\omega L}{e}^{-\frac{R}{2L}t}sin(\omega t)$ Prąd w przypadku oscylacyjnym opisany jest funkcją sinusoidalną o amplitudzie zmieniającej się według funkcji wykładniczej. Czynnik $e^{-\frac{R}{2L}t}$ stanowi tłumienie przebiegu sinusoidalnego a jego wartość jest proporcjonalna do wartości rezystancji obwodu RLC. Odwrotność współczynnika tłumienia charakteryzuje stałą czasową $\tau =\frac{2L}{R}$ obwodu RLC z jaką tłumione są drgania sinusoidalne. Wykorzystując podstawowe relacje zachodzące między zmiennymi w obwodzie szeregowym RLC można wyznaczyć pozostałe napięcia w obwodzie w stanie nieustalonym. W przypadku cewki napięcie uzyskuje się przez zróżniczkowanie funkcji opisującej prąd ładowania. $u_L(t)=L\frac{di}{dt}=-\frac{E}{\omega \sqrt{LC}}{e}^{-\frac{R}{2L}t}sin(\omega t-\phi )$ gdzie kąt $\phi$ jest określony relacją $\phi =arctg\frac{\omega }{R/2L}$ Napięcie na kondensatorze wyznaczyć można bezpośrednio z prawa napięciowego Kirchhoffa zastosowanego do obwodu rzeczywistego z rys. trzeciega na slajdzie 10. $u_C(t)=E-u_L(t)-Ri(t)=$ $=E-\frac{E}{\omega L}{e}^{-\frac{R}{2L}t}[Rsin(\omega t)-\sqrt{\frac{L}{C}}sin(\omega t-\phi )]$

---

Na slajdzie 29 przedstawiono przebiegi prądu i napięć w stanie nieustalonym w obwodzie RLC przy wystąpieniu przypadku oscylacyjnego, czyli przy $R<2\sqrt{\frac{L}{C}}$. Przebieg prądu ma charakter sinusoidalny, tłumiony wykładniczo do zera. Obwiednie przebiegu prądu są wyznaczone funkcjami $f(t)=\pm \frac{E}{\omega L}{e}^{-\frac{R}{2L}t}$ . Przy zasilaniu obwodu RLC napięciem stałym wytworzyły się drgania własne o pulsacji $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$. Pulsacja ta zależy wyłącznie od parametrów obwodu RLC. Głównym czynnikiem regulującym wartość pulsacji wobec małej wartości rezystancji R dla przypadku oscylacyjnego jest wartość indukcyjności L oraz pojemności C. Przy danych wartościach L, C i regulowanej rezystancji, pulsacja rośnie przy malejącej wartości rezystancji.

---

Drgania w obwodzie powstają na skutek wymiany energii między polem elektrycznym kondensatora a polem magnetycznym cewki. Na skutek skończonej wartości rezystancji zachodzi rozpraszanie energii w postaci ciepła wydzielanego na rezystorze. Stąd oscylacje powstające w obwodzie mają charakter malejący. Szybkość tłumienia określa stała tłumienia $\alpha =\frac{R}{2L}$. Im większa wartość rezystancji tym większe tłumienie w obwodzie i szybsze zanikanie drgań sinusoidalnych do zera. Na slajdzie 30 przedstawiono przykładowe przebiegi ładowania kondensatora w obwodzie RLC dla przypadków oscylacyjnych przy zmieniającej się wartości rezystancji. Widoczne jest, że im mniejsza wartość rezystancji tym dłużej trwa stan przejściowy w obwodzie. Wobec małych wartości rezystancji wynikających z warunku występowania przypadku oscylacyjnego jej wpływ na częstotliwość drgań własnych obwodu (wzór ostatni na slajdzie 27) jest stosunkowo niewielki.

---

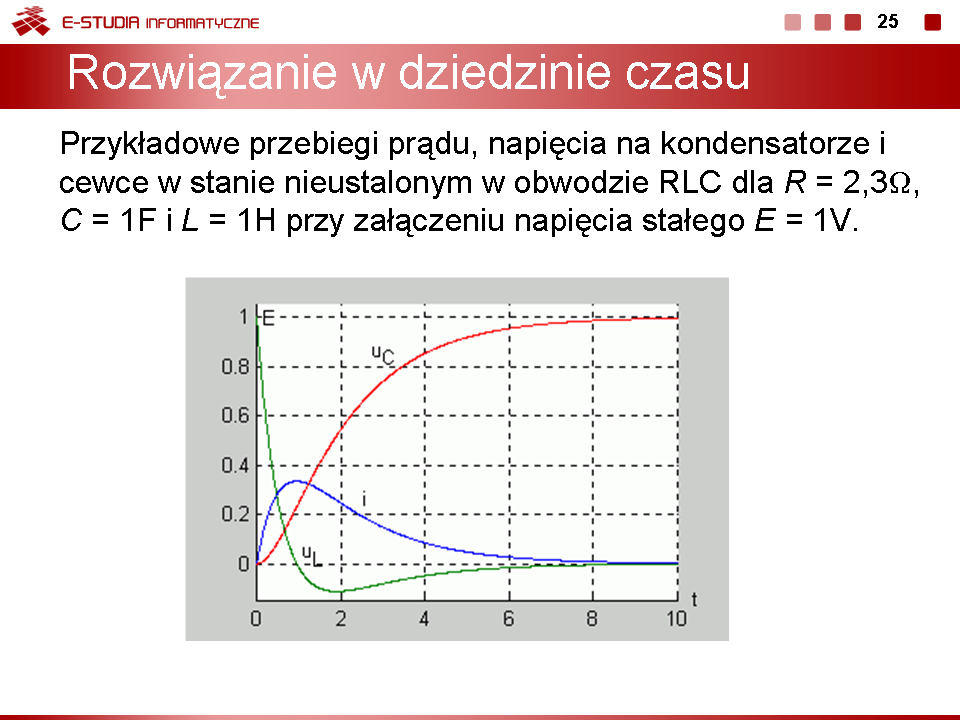
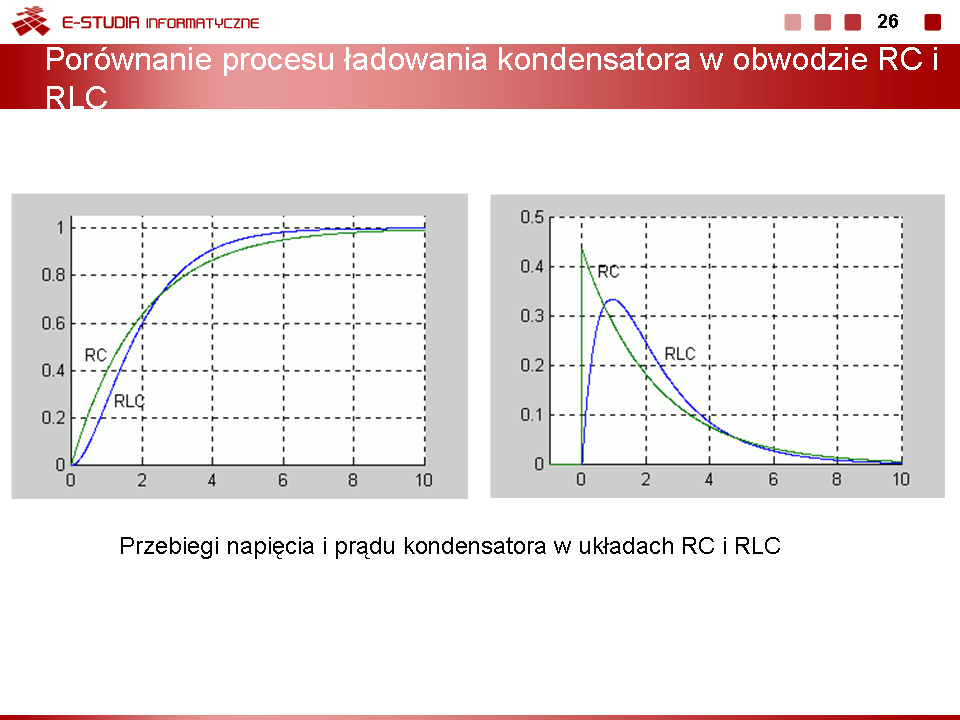
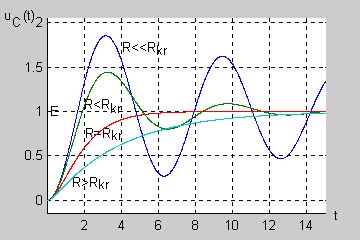
NOTATKI BEZ SLAJDÓW Należy podkreślić, że jakkolwiek wyrażenia analityczne opisujące przebiegi czasowe w obwodzie dla różnych przypadków tłumienia są znacznie różniące się miedzy sobą, wszystkie reprezentują charakter ciągły. Poszczególne przypadki przechodzą w siebie nawzajem przy ciągłej zmianie wartości rezystancji. Przy małej rezystancji tłumienie jest małe i przebieg prądu oraz napięć jest oscylacyjny, tłumiony wykładniczo. Wzrost wartości rezystancji powoduje wzrost tłumienia, drgania trwają krócej aż przy pewnej wartości krytycznej $R_{kr}=2\sqrt{\frac{L}{C}}$ przechodzą w przebieg aperiodyczny (krytyczny), przy którym nie obserwuje się już drgań. Dalszy wzrost rezystancji niewiele zmienia w charakterze jakościowym przebiegów poza wydłużeniem stanu przejściowego. Ilustrację powyższego zjawiska na przykładzie napięcia w obwodzie przedstawiono na rys. poniższym Zadania sprawdzające Zadanie 8.1 Wyznaczyć transformatę odwrotną Laplace’a dla transmitancji operatorowej F(s) $F(s)=\frac{s}{(s+2)(s+3)(s+5{)}^2}$ Rozwiązanie W rozważanym przypadku wszystkie bieguny są rzeczywiste, przy czym jeden z nich jest podwójny. Ich wartości są równe: $s_1=-2$, $s_2=-3$, $s_3=s_4=-5$. Najskuteczniejszą metodą pozostaje w tym przypadku metoda residuów, zgodnie z którą $f(t)=re{s}_{s\to -2}F(s)e^{st}+re{s}_{s\to -3}F(s)e^{st}+re{s}_{s\to -5}F(s)e^{st}$ Wartość funkcji residuum dla poszczególnych biegunów jest równa $re{s}_{s\to -2}F(s)e^{st}=\underset{s\to -2}{\lim }F(s)(s+2)e^{st}=-\frac{2}{9}{e}^{-2t}$ $re{s}_{s\to -3}F(s)e^{st}=\underset{s\to -3}{\lim }F(s)(s+3)e^{st}=\frac{3}{4}{e}^{-3t}$ $re{s}_{s\to -5}F(s)e^{st}=\underset{s\to -5}{\lim }\frac{d}{ds}(F(s)(s+5{)}^2{e}^{st})=-\frac{19}{36}{e}^{-5t}-\frac{5}{6}t{e}^{-5t}$ Sumując poszczególne składniki otrzymujemy $f(t)=-\frac{2}{9}{e}^{-2t}+\frac{3}{4}{e}^{-3t}-\frac{19}{36}{e}^{-5t}-\frac{5}{6}t{e}^{-5t}$ Zadanie 8.2 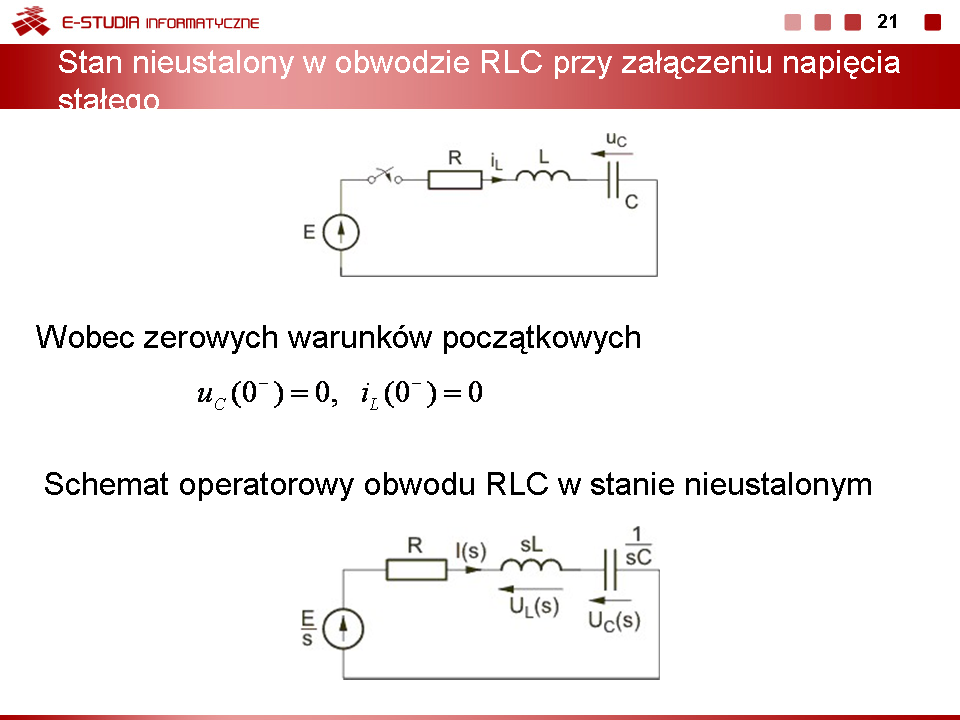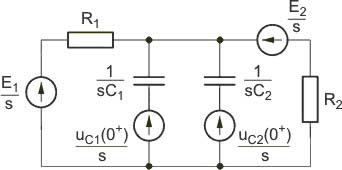Określić przebieg napięcia na kondensatorze w stanie nieustalonym po przełączeniu metodą operatorową w obwodzie przedstawionym na rys. poniższym. Przyjąć następujące parametry obwodu:$R_1=50\mathrm{\Omega }$, $R_2=100\mathrm{\Omega }$, $C_1=10\mu F$, $C_2=20\mu F$, $e_1(t)=50V$, $e_2(t)=100V$. Rozwiązanie Warunki początkowe: $u_{C1}(0^{-})=e_1=50$, $u_{C2}(0^{-})=e_2=100$ Ze względu na wymuszenie stałe nie zachodzi potrzeba stosowania metody superpozycji stanu. Schemat operatorowy obwodu w stanie nieustalonym przedstawiony jest na rys. poniższym Z metody potencjałów węzłowych zastosowanych do obwodu z rys. 9.18 wynika $U_C(s)=\frac{\frac{50}{50s}+\frac{100}{100s}+10^{-5}{u}_{C1}(0^{+})+2\cdot 10^{-5}{u}_{C2}(0^{+})}{1/50+1/100+s10^{-5}+2s10^{-5}}$ $U_C(s)=\frac{250s+2,5\cdot 10^{-5}}{3s(s+1000)}$ Bieguny układu: $s_1=0$, $s_2=1000$ Transformata odwrotna Laplace’a $u_C(t)=\underset{s\to 0}{\lim }{U}_C(s)s{e}^{st}+\underset{s\to 1000}{\lim }{U}_C(s)(s+1000)e^{st}$ $u_C(t)=\frac{250}{3}+\frac{50}{3}{e}^{-1000t}$ W stanie ustalonym przy $t\to \mathrm{\infty }$ mamy $u_{Cu}(t)=\frac{250}{3}V$. Zauważmy, że w wyniku przełączenia napięcia na kondensatorach w chwili t=0 uległy skokowej zmianie (w obwodzie powstało oczko złożone z samych kondensatorów). Zadanie 8.3 Wartości indukcyjności i pojemności w obwodzie szeregowym RLC są równe: $L=0,01H$ oraz $C=1\mu F$. Określić zmiany częstotliwości drgań własnych tego obwodu w funkcji wartości rezystancji R zmieniającej się od zera do rezystancji krytycznej. 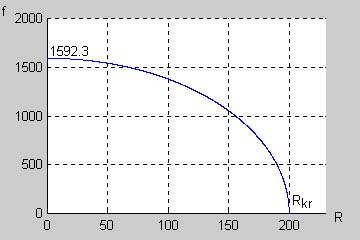Rozwiązanie Częstotliwość drgań własnych obwodu szeregowego RLC dana jest wzorem $f=\frac{1}{2\pi }\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}=\frac{1}{2\pi }\sqrt{10^8-0,25\cdot 10^4{R}^2}$ Rezystancja krytyczna $R_{kr}=2\sqrt{\frac{L}{C}}=200\mathrm{\Omega }$ Na rys. ponizszym przedstawiono zależność częstotliwości drgań własnych obwodu od wartości rezystancji R w podanym zakresie zmian rezystancji