Inżynieria oprogramowania

Zadania – Metody formalne, sieci Petriego

<< Powrót do strony zadań

Odpowiedzi

Zadanie 1:

• T0, T1, T3, T4, T1
• T0, T1, T3, T2, T4, T1
• T0, T1, T2, T1, T3
• T0, T1, T2, T3, T4, T1

<flashwrap>file=io-07-lab01.swf|width=360|height=350</flashwrap>

T0, T1, T3, T2, T4, T1

<flashwrap>file=io-07-lab02.swf|width=360|height=350</flashwrap>

T0, T1, T2, T3, T4, T1

Zadanie 2:

• T1, T3, T5, T0, T3
• T1, T3, T5, T2, T0, T3
• T0, T3, T5, T1, T2
• T0, T2, T3, T5, T4
• T2, T0, T3, T5, T1, T4
• T2, T0, T3, T4, T1

<flashwrap>file=io-07-lab03.swf|width=380|height=370</flashwrap>

T1, T3, T5, T2, T0, T3

<flashwrap>file=io-07-lab04.swf|width=380|height=370</flashwrap>

T0, T2, T3, T5, T4

<flashwrap>file=io-07-lab05.swf|width=380|height=370</flashwrap>

T2, T0, T3, T5, T1, T4

Zadanie 3:

• ( T0 T1 T2 T6 ( T4 T6 )* T3 T5 )*

Zadanie 4:

Plik w formacie PIPE2

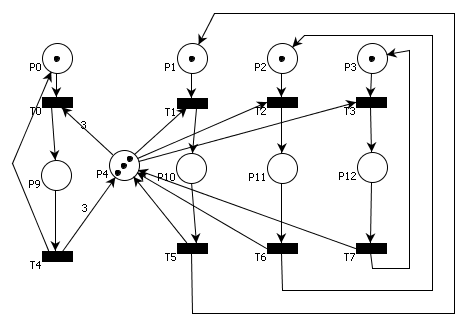
Rozwiązanie przedstawiono na rysunku 5.

Rys. 5. Sieć Petriego do zadania 4

<flashwrap>file=io-07-lab05.swf|width=460|height=320</flashwrap>