Matematyka dyskretna 1/Ćwiczenia 5: Współczynniki dwumianowe

Współczynniki dwumianowe

Ćwiczenie 1

Wskaż największy wyraz w $n$ -tym wierszu Trójkąta Pascala i odpowiedź uzasadnij.

Wskazówka

Największym wyrazem w $n$ -tym wierszu jest wyraz środkowy $(\binom{n}{⌊ n / 2 ⌋}) = (\binom{n}{⌈ n / 2 ⌉})$ . Korzystając ze wzoru na postać zwartą współczynnika dwumianowego, pokaż $(\binom{n}{k}) < (\binom{n}{k + 1})$ dla $k < ⌊ n / 2 ⌋$ .

Rozwiązanie

Ponieważ $(\binom{n}{k}) = (\binom{n}{n - k})$ , dla $n ⩾ k ⩾ 0$ , to aby pokazać, że największym wyrazem w $n$ -tym wierszu jest $(\binom{n}{⌊ n / 2 ⌋}) = (\binom{n}{⌈ n / 2 ⌉})$ , wystarczy pokazać, że

(\binom{n}{k}) < (\binom{n}{k + 1})

,

dla $k < ⌊ \frac{n}{2} ⌋$ . Nierówność ta jest równoważna kolejno

\begin{aligned} \frac{n!}{k! (n - k)!} & < \frac{n!}{(k + 1)! (n - k - 1)!}, \\ \frac{1}{n - k} & < \frac{1}{k + 1}, \\ k + 1 & < n - k, \\ k & < \frac{n - 1}{2} . \end{aligned}

Ostatnia nierówność zachodzi dla $k < ⌊ \frac{n}{2} ⌋$ , zatem wszystkie poprzednie też zachodzą.

Ćwiczenie 2

Posługując się interpretacją kombinatoryczną pokaż, że

(\binom{n}{0}) (\binom{n}{k}) + (\binom{n}{1}) (\binom{n - 1}{k - 1}) + \dots + (\binom{n}{k}) (\binom{n - k}{0}) = 2^{k} (\binom{n}{k})

Wskazówka

Rozważ liczbę kolorowań $k$ rozróżnialnych obiektów wybranych spośród $n$ , przy użyciu dwu kolorów.

Rozwiązanie

Policzmy kolorowania $k$ rozróżnialnych obiektów wybranych spośród $n$ , przy użyciu dwu kolorów (biały i czarny). Podzbiór $k$ -elementowy $n$ -elementowego zbioru obiektów można wybrać na $(\binom{n}{k})$ sposobów i każdy taki podzbiór możemy pokolorować na $2^{k}$ sposobów. Zatem liczba interesujących nas kolorowań to $2^{k} (\binom{n}{k})$ .

Policzmy nasze kolorowania inną metodą. Zauważmy, iż dowolne kolorowanie posiada $i$ obiektów białych i $k - i$ czarnych dla pewnego $i \in {0, \dots, k}$ . Zatem każde kolorowanie możemy jednoznacznie otrzymać wybierając najpierw $i$ obiektów spośród wszystkich $n$ (i kolorując je na biało), a później z pozostałych $n - i$ obiektów wybierając $k - i$ (kolorując je na czarno). Możemy to zrobić na $(\binom{n}{i}) (\binom{n - i}{k - i})$ sposobów, czyli sumując po wszystkich możliwych wartościach $i$ otrzymujemy $\sum_{i = 0}^{k} (\binom{n}{i}) (\binom{n - i}{k - i})$ .

Ćwiczenie 3

Posługując się interpretacją kombinatoryczną pokaż, że

{(\binom{n}{0})}^{2} + {(\binom{n}{1})}^{2} + \dots + {(\binom{n}{n})}^{2} = (\binom{2 n}{n})

Wskazówka

Rozważ liczbę wyborów $n$ osób z $2 n$ -osobowej grupy złożonej z $n$ mężczyzn i $n$ kobiet.

Rozwiązanie

Rozważmy na ile sposobów możemy wybrać $n$ osób z grupy $n$ mężczyzn i $n$ kobiet. Oczywiście, z jednej strony, sposobów wyboru $n$ spośród $2 n$ osób jest $(\binom{2 n}{n})$ . Alternatywnie zauważmy, że wybierając $n$ osób wybieramy $i$ mężczyzn i $n - i$ kobiet dla pewnego $i \in {0, \dots, n}$ . Dla ustalonego $i$ możemy to wykonać na $(\binom{n}{i}) (\binom{n}{n - i}) = {(\binom{n}{i})}^{2}$ sposobów, zatem sumarycznie liczba możliwości to $\sum_{i = 0}^{n} {(\binom{n}{i})}^{2}$ , co było do pokazania.

Ćwiczenie 4

Posługując się interpretacją kombinatoryczną pokaż, że

(\binom{n}{1}) + 2 (\binom{n}{2}) + \dots + n (\binom{n}{n}) = n 2^{n - 1}

Wskazówka

Rozważ liczbę wyborów z grupy $n$ osób podzbioru z wyznaczonym w nim przywódcą.

Rozwiązanie

Rozważmy na ile sposobów można wybrać z grupy $n$ osób podzbiór z wyznaczonym w nim przywódcą. Z jednej strony możemy najpierw wybrać przywódcę spośród $n$ osób, a później dobrać do niego dowolny podzbiór zbioru pozostałych $n - 1$ osób. Możemy to zrobić na $n 2^{n - 1}$ sposobów.

Z drugiej strony możemy najpierw wybrać niepusty podzbiór $i$ -elementowy (dla $i \in {1, \dots, n}$ ) zbioru $n$ osób, a potem wybrać spośród nich przywódcę na jeden z $i$ sposobów. Sumując po wszystkich $i$ możemy wykonać to na $\sum_{i = 0}^{n} i (\binom{n}{i})$ sposobów, co było do pokazania.

Ćwiczenie 5

Posługując się interpretacją kombinatoryczną pokaż, że

1^{2} {(\binom{n}{1})}^{2} + 2^{2} {(\binom{n}{2})}^{2} + \dots + n^{2} {(\binom{n}{n})}^{n} = n^{2} (\binom{2 n - 2}{n - 1})

Wskazówka

Rozważ liczbę wyborów z grupy $2 n$ osobowej złożonej z $n$ mężczyzn i $n$ kobiet podzbioru, w którym liczba kobiet i mężczyzn jest równa i ponadto, w którym wyróżnionych jest dwóch przywódców jeden mężczyzna i jedna kobieta.

Rozwiązanie

Dla rozgrzewki rozważmy, na ile sposobów z grupy $2 n$ osób złożonej z $n$ mężczyzn i $n$ kobiet można wybrać podzbiór osób, w którym liczba mężczyzn i kobiet jest równa. Nietrudno zauważyć, iż jest to $\sum_{i = 0}^{n} {(\binom{n}{i})}^{2}$ , a z Ćwiczenia 3 wiemy, że $\sum_{i = 0}^{n} {(\binom{n}{i})}^{2} = (\binom{2 n}{n})$ .

Zastanówmy się teraz z kolei na ile sposobów można wybrać z tej samej $2 n$ osobowej grupy podzbiór, w którym liczba mężczyzn i kobiet jest równa i dodatkowo wśród wybranych jest wyróżnionych dwóch przywódców: jeden mężczyzna i jedna kobieta.

Dla ustalonego $i \in {1, \dots, n}$ możemy najpierw wybrać $i$ kobiet i $i$ mężczyzn na ${(\binom{n}{i})}^{2}$ sposobów, a potem spośród nich wyłonić przywódców na $i^{2}$ sposobów. Zatem sumarycznie możemy dokonać wyboru na $\sum_{i = 1}^{n} i^{2} {(\binom{n}{i})}^{2}$ .

Alternatywnie możemy najpierw wybrać przywódcę jednego spośród $n$ mężczyzn i jednej spośród $n$ kobiet na $n^{2}$ sposobów, a potem uzupełnić wybrańców dobierając im $i$ mężczyzn i tyle samo kobiet, dla $i \in {0, \dots, n - 1}$ . Z początkowej naszej refleksji możemy to zrobić na $(\binom{2 n - 2}{n - 1})$ sposobów. Podsumowując, interesującego nas wyboru możemy dokonać na $n^{2} (\binom{2 n - 2}{n - 1})$ , co było do pokazania.

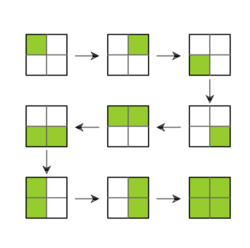
Ćwiczenie 6

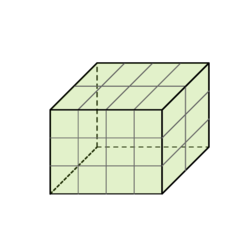
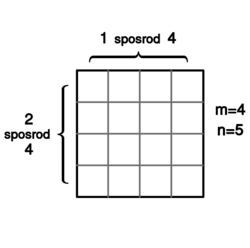
Ile prostokątów zawiera się w kratce $n \times n$ ? Dla przykładu w kratce $2 \times 2$ jest ich $9$ .

Wskazówka

Rozważ ile prostokątów w kratce $n \times n$ zawiera się w górnej lewej podkratce $m \times m$ (dla $m < n$ ), ale nie zawiera się w górnej lewej podkratce $(m - 1) \times (m - 1)$ .

Rozwiązanie

Policzmy ile prostokątów w kratce $n \times n$ położonych jest w lewej górnej podkratce $m \times m$ i przylega do chociaż jednej z wewnętrznych (czyli dolnej bądź prawej) krawędzi podkratki. Kilka przykładów takich prostokątów przedstawiamy poniżej dla $n = 5$ i $m = 4$ :

Prostokąt przylegający do prawej pionowej krawędzi podkratki $m \times m$ i nieprzylegający do dolnej poziomej krawędzi jest jednoznacznie wyznaczony przez wybór $1$ pionowej krawędzi spośród $m$ i dwu poziomych krawędzi spośród $m$ .

Zatem jest dokładnie $(\binom{m}{1}) (\binom{m}{2}) = \frac{m^{2} (m - 1)}{2}$ takich prostokątów. Analogicznie jest $\frac{m^{2} (m - 1)}{2}$ prostokątów przylegających do dolnej krawędzi podkratki $m \times m$ i nieprzylegających do prawej. W końcu jest dokładnie $m^{2}$ prostokątów leżących w prawym dolnym narożniku podkratki $m \times m$ , gdyż są one jednoznacznie wyznaczone przez wybór $1$ poziomej linii spośród $m$ i $1$ pionowej linii spośród $m$ .

Zatem w sumie jest

$\frac{m^{2} (m - 1)}{2} + \frac{m^{2} (m - 1)}{2} + m^{2} = m^{3}$ ,

prostokątów w podkratce $m \times m$ przylegających do chociaż jednej wewnętrznej krawędzi. Sumując po $m \in {1, \dots, n}$ otrzymujemy liczbę wszystkich prostokątów w kratce $n \times n$ , czyli jest ich

$1^{3} + 2^{3} + \dots + n^{3} = {(\frac{n (n + 1)}{2})}^{2}$

Ćwiczenie 7

Udowodnij, że:

$(- 4)^{n} (\binom{- \frac{1}{2}}{n}) = (\binom{2 n}{n})$

Wskazówka

Rozwiązanie

Dowód przez indukcję względem $n$ . Dla $n = 1$ mamy

$(- 4)^{1} (\binom{- \frac{1}{2}}{1}) = (- 4) \frac{- \frac{1}{2}}{1} = 2 = (\binom{2}{1})$

Ponadto:

$\begin{aligned} (\binom{2 (n + 1)}{n + 1}) & = \frac{(2 n + 1) (2 n + 2)}{(n + 1)^{2}} (\binom{2 n}{n}) \\ = \frac{2 (2 n + 1)}{n + 1} (- 4)^{n} (\binom{- \frac{1}{2}}{n}) \\ = (- 4)^{n + 1} \frac{(- \frac{1}{2} - n)}{n + 1} (\binom{- \frac{1}{2}}{n}) \\ = (- 4)^{n + 1} (\binom{- \frac{1}{2}}{n + 1}) . \end{aligned}$

Ćwiczenie 8

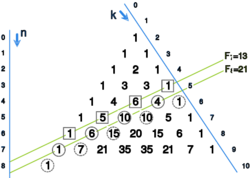
Udowodnij, że:

$f_{n + 1} = \sum_{k = 0}^{n} (\binom{n - k}{k})$

gdzie $f_{n}$ jest $n$ -tą liczbą Fibonacci'ego

Wskazówka

Rozwiązanie

Dowód indukcyjny względem $n$ . Dla $n = 0$ i $n = 1$ mamy odpowiednio $f_{1} = 1 = (\binom{0}{0}) = 1$ i $f_{2} = 1 = 1 + 0 = (\binom{1}{0}) + (\binom{0}{1})$ . Ponadto:

$\begin{aligned} f_{n + 2} & = f_{n} + f_{n + 1} \\ = \sum_{k = 0}^{n - 1} (\binom{n - 1 - k}{k}) + \sum_{k = 0}^{n} (\binom{n - k}{k}) \\ = (\binom{n}{0}) + \sum_{k = 0}^{n - 1} ((\binom{n - 1 - k}{k}) + (\binom{n - (k + 1)}{k + 1})) \\ = (\binom{n}{0}) + \sum_{k = 0}^{n - 1} (\binom{n - k}{k + 1}) \\ = (\binom{n + 1}{0}) + \sum_{k = 1}^{n} (\binom{n + 1 - k}{k}) + 0 \\ = \sum_{k = 0}^{n} (\binom{n + 1 - k}{k}) + (\binom{0}{n + 1}) \\ = \sum_{k = 0}^{n + 1} (\binom{n + 1 - k}{k}) . \end{aligned}$

Matematyka dyskretna 1/Ćwiczenia 5: Współczynniki dwumianowe

Współczynniki dwumianowe

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia