GKIW Moduł 4
Z Studia Informatyczne

|

|

|
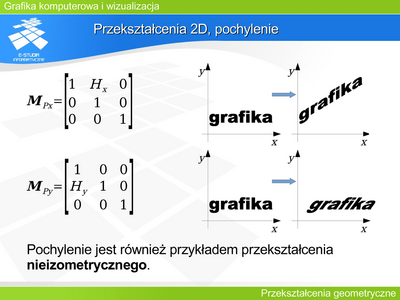
Przekształcenia 2D, obrót, problem przesunięcia II
Niech . Niech wektor opisuje translację punktu na płaszczyźnie. Czy można znaleźć takie a, b, c, d, aby dla i . |

|

|
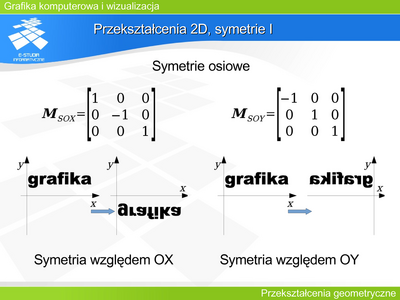
|
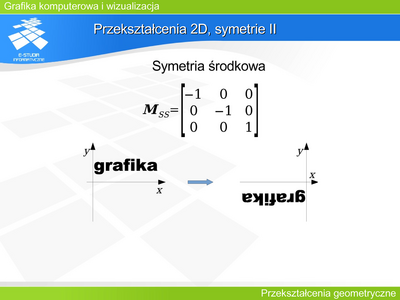
|

|
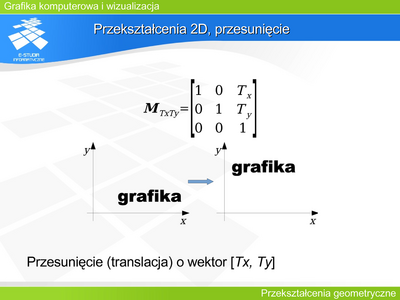
|
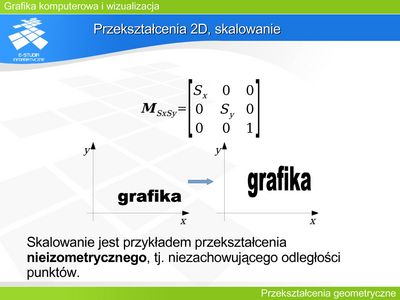
|
|
|

|
|
|
|
|
|

|
|
|
|
|
|
|

|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
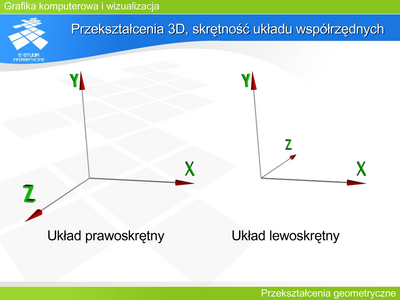
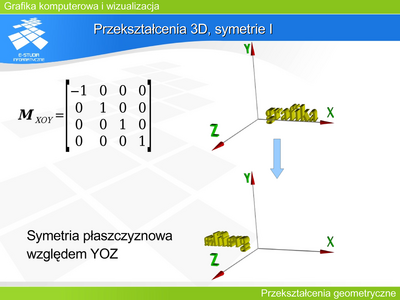
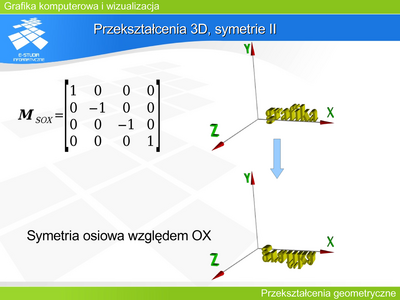
Przekształcenia 2D, obrót, problem przesunięcia II
Niech . Niech wektor opisuje translację punktu na płaszczyźnie. Czy można znaleźć takie a, b, c, d, aby dla i . |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|