| 14.4 Elektromagnetyczne drgania swobodne
Modelowym układem fizycznym, w którym zachodzić mogą elektromagnetyczne drgania harmoniczne swobodne jest zamknięty obwód elektryczny o oporności równej zeru, zawierający zwojnicę o indukcyjności i kondensator o pojemności .
W obwodzie przedstawionym na rysunku kondensator został naładowany ładunkiem . Gdy w chwili zamkniemy obwód, to kondensator zacznie się rozładowywać i zmieniający się prąd rozładowania spowoduje powstanie w zwojnicy siły elektromotorycznej samoindukcji. Stan fizyczny obwodu można opisać za pomocą II prawa Kirchhoffa:
- gdzie
Po podstawieniach i przekształceniach otrzymujemy równanie elektromagnetycznego oscylatora harmonicznego swobodnego
Rozwiązaniem tego równania, spełniającym warunki początkowe: , jest funkcja
- Parser nie mógł rozpoznać (nieznana funkcja „\dispaystyle”): {\displaystyle \dispaystyle q(t)=q_0 cos\omega_0 t}
gdzie: Parser nie mógł rozpoznać (nieznana funkcja „\dispaystyle”): {\displaystyle \dispaystyle \omega_0=\sqrt{\displaystyle \frac{1}{LC}}}
- częstość drgań swobodnych, - faza drgań, - amplituda drgań.
Mając funkcję można obliczyć napięcie na kondensatorze , natężenie prądu oraz napięcie na zwojnicy :
Warto zauważyć, że napięcia na kondensatorze i zwojnicy mają równe amplitudy i przeciwne fazy (przesunięcie fazowe wynosi ), zaś natężenie prądu jest przesunięte w fazie o .
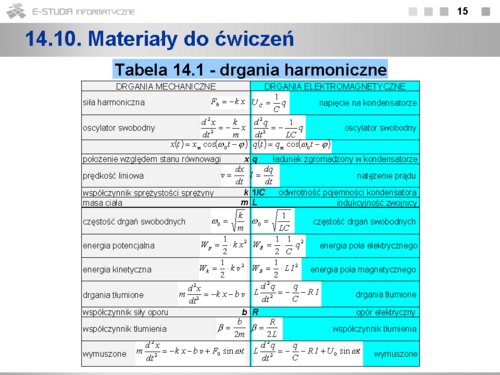
Z powyższej analizy wynika, że po dostarczeniu do obwodu LC porcji energii (naładowanie kondensatora) i braku dalszej ingerencji zewnętrznej, zachodzą w nim drgania harmoniczne swobodne - wielkości opisujące stan układu są funkcjami harmonicznymi. Porównanie z mechanicznym oscylatorem harmonicznym swobodnym (np. klocek o masie m zaczepiony do sprężyny o współczynniku sprężystości k) pokazuje, że ładunek na kondensatorze jest wielkością analogiczną do wychylenia z położenia równowagi a natężenie prądu do prędkości. Pełne zestawienie analogii między drganiami elektromagnetycznymi i drganiami mechanicznymi przedstawiono w tabeli nr 14.1.
Okres i częstotliwość drgań swobodnych (inaczej drgań własnych) obwodu LC są równe:
- Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle \displaystyle T_0=\frac{2\pi}{\omeha_0}=2\pi \sqrt{LC}}
Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc i energię pola elektrycznego w kondensatorze
oraz moc i energię pola magnetycznego w zwojnicy
Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <mathpi/2\,</math>. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy
jest stała i równa energii dostarczonej do obwodu.
Z powyższych rozważań wynika, że elektromagnetyczne drgania swobodne w obwodzie LC można traktować jak okresowe przemiany energii pola elektrycznego w kondensatorze w energię pola magnetycznego w zwojnicy i na odwrót. Okres tych przemian jest równy połowie okresu drgań własnych czyli okresu zmienności napięć na kondensatorze i zwojnicy oraz natężenia prądu. W rzeczywistych obwodach elektrycznych występuje zawsze niezerowy opór elektryczny, a więc wydziela się energia cieplna. W takim przypadku energia układu drgającego maleje i po pewnym czasie drgania zanikają.
|