Na podstawie grafu konstruujemy graf dwudzielny w następujący sposób:
Parser nie mógł rozpoznać (nieznana funkcja „\begin{array}”): {\displaystyle \begin{array}{r@{}c@{}l} V^k_{out} &:=& \{v_{out} : v \in V\, \ v\neq s\} \cup \{s_{out}^{i} : 1\le i \le k\},\\ V^k_{in} &:=& \{v_{in} : v \in V\, \ v\neq t\} \cup \{t_{in}^{i} : 1\le i \le k\},\\ E^k_{out,in} &:=& \{v_{out} u_{in} : (v,u) \in V, \ v \neq s,\ u\neq t\} \cup\\ &\cup& \{v_{out}v_{in} : v \in V\}\cup\\ &\cup& \{s_{out}^i u_{in} : (s,u) \in V, \ 1\le i \le k\}\cup\\ &\cup& \{v_{out} t_{in}^i : (v,t) \in V, \ 1\le i \le k\}.\\ \end{array} }
Konstrukcja ta jest przedstawiona na poniższym rysunku a) przykładowy graf b) graf skonstruowany na podstawie grafu .
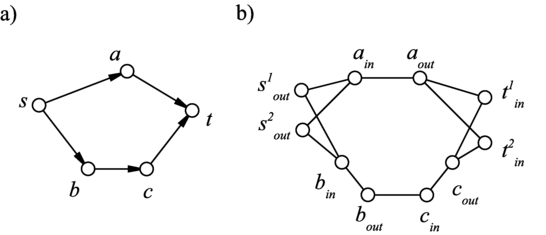
Zauważ, że jeżeli w grafie istnieje doskonałe skojarzenie to w grafie istnieje rozłącznych wierzchołkowo ścieżek z do . Jest tak ponieważ każde doskonałe skojarzenie w koduje zbiór wierzchołkowo rozłącznych ścieżek z do . Krawędzie wybrane do doskonałego skojarzenia kodują krawędzie wchodzące do i wychodzące z wierzchołka . Krawędź wchodząca z jest kodowana przez krawędź kojarzącą wierzchołek , a krawędź wychodząca kodowana jest przez krawędź kojarzącą . Odczytując skojarzenie w ten sposób dostajemy zbiór ścieżek zaczynających się w i kończących w oraz ewentualnie pewien zbiór cykli. W drugą stronę łatwo zauważyć, że z każdego zbioru rozłącznych ścieżek możemy skonstruować doskonałe skojarzenie w grafie .
W celu wyznaczenia liczby wierzchołkowo rozłącznych ścieżek w możemy przy pomocy binarnego wyszukiwania znaleźć największe dla którego zawiera doskonałe skojarzenie. Liczbę można też wyznaczyć nie używając wyszukiwania binarnego. Rozważmy graf , oraz załóżmy, że w jest w nim wierzchołkowo rozłącznych ścieżek. Używając kodowania opisanego powyżej możemy skonstruować w skojarzenie o liczności . Weźmy teraz maksymalne skojarzenie w i przyjrzyjmy się zbiorowi ścieżek jaki ono koduje w . Zauważmy, że jeżeli ścieżka wychodząca z wierzchołka urywa się nagle, to można ja usunąć nie zmieniając liczności skojarzenie , te same wierzchołki można skojarzyć krawędziami postaci , które odpowiadają jednoelementowym cyklom.
