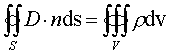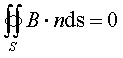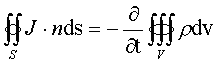TTS Moduł 2

Wykład

---

---

• WPROWADZENIE - WIELKOŚCI CHARAKTERYZUJĄCE POLE EM

Pola elektryczne i magnetyczne kiedy zmieniają się, to powiązane są ze sobą wieloma związkami, nazwanymi wspólnie równaniami Maxwella. Równania te oparte są na wielu fizycznych eksperymentach prowadzonych przez uczonych całe dziesięciolecia. Równania Maxwella pełnią rolę fundamentu dla całej techniki mikrofalowej, tworzonej i rozwijanej przez ostatnie 100 lat.

Równania Maxwella wiążą ze sobą najważniejsze wielkości pola elektromagnetycznego. Zajmiemy się przestrzenią wypełnioną jednorodnym, izotropowym ośrodkiem, charakteryzowanym przez :

• Przenikalność elektryczna ośrodka $\epsilon$ , w próżni równa $\epsilon \equiv {\epsilon }_0=10^{-9}/36\pi [F/m]$ .
• Przenikalność magnetyczna ośrodka $\mu$ , w próżni równa $\mu \equiv {\mu }_0=4\pi \cdot 10^{-7}[H/m]$ .
• Przewodność właściwa ośrodka $\sigma$ (konduktywność), jej miarą jest $[S/m]$, w próżni $\sigma =0$ .

Pole elektromagnetyczne jest kompozycją pól elektrycznego i magnetycznego. Charakteryzują go następujące wielkości:

• Natężenie pola elektrycznego $E(x,y,z,t)$ jest wektorem (ma swoją wartość i kierunek), funkcją miejsca i czasu. Natężenie pola elektrycznego mierzymy w woltach na metr $[V/m]$.
• Natężenie pola magnetycznego $H(x,y,z,t)$ jest także wektorem, mierzymy jego wartość w amperach na metr $[A/m]$.
• Indukcja elektryczna $D=\epsilon E$ jest wektorem, w ośrodku izotropowym skierowanym w tą samą stronę, co natężenie pola elektrycznego, w próżni $D={\epsilon }_{0}E$ , mierzymy jej wartość w amperach razy sekunda na metr kwadratowy $[As/m^2]$, czyli kulombach na metr kwadratowy $[C/m^2]$.
• Indukcja magnetyczna $B=\mu H$ jest wektorem, w ośrodku izotropowym skierowanym w tą samą stronę, co natężenie pola magnetycznego, w próżni $B={\mu }_{0}H$ , mierzymy jej wartość w voltach razy sekunda na metr kwadratowy $[Vs/m^2]$.

• RÓWNANIA MAXWELLA

• Całkowa postać równań Maxwella

Jak powiedziano wyżej, równania Maxwella opierają się odkrytych eksperymentalnie prawach fizycznych.

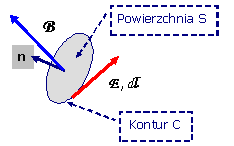
Rys.2.1. Powierzchnia $S$ o konturze $C$ w polu $EM$ o indukcji magnetycznej $B=\mu H$ i natężeniu pola elektrycznego $E$.

Pierwsze prawo Maxwella w postaci całkowej jest zapisem prawa Faradaya. Rozważane są indukcja pola magnetycznego $B=\mu H$ i natężenie pola elektrycznego $E$ w sąsiedztwie powierzchni $S$ otoczonej konturem $C$, co pokazano na rys.2.1.

Pierwsze prawo Maxwella wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię $S$ z polem elektrycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię.

${\oint }_{C}Edl=-\underset{S}{\iint }\frac{\partial B}{\partial t}\cdot nds$ ;

(2-1)

Drugie równanie Maxwella w postaci całkowej (2-2) jest zapisem prawa Ampere’a. Wiąże ono ze sobą prąd płynący przez powierzchnię $S$ z polem magnetycznym $H$ , całkowanym wzdłuż zamkniętego konturu $C$.

${\oint }_{C}Hdl=-\underset{S}{\iint }(J+\frac{\partial D}{\partial t})\cdot nds$ ;

(2-2)

Prawo Gaussa zastosowane dla pola elektrycznego mówi, że strumień wektora indukcji pola elektrycznego $D$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ równy jest zgromadzonemu w tej objętości ładunkowi. Ładunek ten otrzymujemy całkując gęstość tego ładunku $\rho$ mierzoną w kulombach na metr sześcienny w objętości $V$ równanie (2-3).

;

(2-3)

To samo prawo zastosowane do strumienia wektora indukcji pola magnetycznego prowadzi do równanie (1-4),

;

(2-4)

gdyż pole magnetyczne jest bezźródłowe.

Do powyższych równań dodawane jest zapisane w formie całkowej równanie ciągłości prądu

;

(2-5)

Mówi ono, że prąd przewodzenia wypływający przez powierzchnię $S$ zamkniętej objętości $V$ równy jest szybkości zmian ładunku w tej objętości.

• Różniczkowa postać równań Maxwella

Równanie Maxwella w postaci całkowej opisują poparte eksperymentami zachowanie rozmaitych wielkości opisujących pole elektromagnetyczne. Ich interpretacja fizyczna jest czytelna.

$\mathrm{\nabla }\times E=-\frac{\partial B}{\partial t}$  ; $\mathrm{\nabla }\times H=J+\frac{\partial D}{\partial t}$  ; $\mathrm{\nabla }\cdot J=-\frac{\partial \rho }{\partial t}$  ; $\mathrm{\nabla }\cdot D=\rho$  ; $\mathrm{\nabla }\cdot B=0$  ;

(2-6)

Z wielu względów wygodnie jest zapisać te równania w postaci różniczkowej. Otrzymujemy wtedy zestaw równań (2-6).

Pięć powyższych równań podawanych jest tradycyjnie jako równania Maxwella. Z matematycznego punktu widzenia występują związki między nimi, gdyż ostatnie dwa mogą być wyprowadzone w oparciu o pierwsze trzy. Z opisowego punktu widzenia pozostawimy w tym miejscu wszystkie z nich.

• Równanie Maxwella w notacji zespolonej

Przyjmiemy teraz założenie, że natężenia pól elektrycznego i magnetycznego oraz prądy zmieniają się sinusoidalnie w czasie. Pozwala to wprowadzić notację zespoloną. Zespolone wektory $E,D,H,B$ i $J$ związane są z wektorami rzeczywistymi zależnościami w formie (2-7).

$E(x,y,z,t)=Re\{E(x,y,z)exp(j\omega t)\}$  ;

(2-7)

W praktyce takie w przeważającej liczbie przypadków powyższe założenia są spełnione.

Pochodne po czasie wielkości zmiennych sinusoidalnie, czasami mówimy harmonicznie, w czasie obliczamy zgodnie z regułą (2-8):

$\frac{\partial e^{j\omega t}}{\partial t}=j\omega e^{j\omega t}$  ;

(2-8)

Pozwala to zapisać równania Maxwella w innej, uproszczonej formie, w której usunięto zależność występujących w nich zmiennych od czasu. W notacji zespolonej podawane są zwykle tylko cztery z nich.

$\mathrm{\nabla }\times E=-j\omega B$  ; $\mathrm{\nabla }\times H=J+j\omega D$  ; $\mathrm{\nabla }\cdot D=\rho$  ; $\mathrm{\nabla }\cdot B=0$  ;

(2-9)

Dla ośrodka jednorodnego, w którym nie ma ładunków i prądów przewodzenia równania powyższe upraszczają się do postaci (2-10):

$\mathrm{\nabla }\times E=-j\omega B$  ; $\mathrm{\nabla }\times H=j\omega D$  ; $\mathrm{\nabla }\cdot D=0$  ; $\mathrm{\nabla }\cdot B=0$  ;

(2-10)

• POLA W OŚRODKACH I WARUNKI BRZEGOWE

• Rodzaje ośrodków

W poprzednim punkcie założyliśmy, że pola elektryczne i magnetyczne występują w nieograniczonym ośrodku. Dokonajmy przeglądu ośrodków ze względu na własności elektryczne, które określają postać zależności między wektorami $E,D,H,B$ i $J$. W szerokiej klasie ośrodków zależności między tymi wektorami można zapisać w postaci tzw. równań materiałowych

$D=\epsilon E$  ; $B=\mu H$  ; $J=\sigma E$  ;

(2-11)

Przypomnijmy, że wartości $\epsilon ,\mu ,\sigma$ charakteryzujące ośrodek to przenikalność elektryczna, przenikalność magnetyczna oraz konduktywność, czyli parametry materiałowe ośrodka.

Związki (2-11) wskazują na liniową zależność wektorów indukcji oraz gęstości prądu od natężeń pól. Oznacza to, że wielkości $\epsilon ,\mu ,\sigma$ nie zależą od natężeń pól i taki ośrodek nazywamy liniowym. Jeżeli przynajmniej jeden z parametrów ośrodka zależy od natężeń pól, to zależności (2-11) nie są już liniowe i ośrodek nazywa się nieliniowym.

Ośrodek jest jednorodny gdy jego parametry nie zależą od współrzędnych punktu. W przeciwnym przypadku mówimy o ośrodku niejednorodnym.

Istnieją ośrodki, których parametry $\epsilon ,\mu ,\sigma$ zależą od częstotliwości. Ośrodki takie nazywamy dyspersyjnymi. Równania materiałowe w formie (2-11) mają sens dla ośrodków dyspersyjnych tylko w przypadku sinusoidalnej zależności pól od czasu. Dla dowolnej zależności pól od czasu związki (2-11) są słuszne dla transformat fourierowskich wektorów $E,D,H,B,J$.

Jeżeli wielkości $\epsilon ,\mu ,\sigma$ są niezależne od kierunku pól, to parametry te są skalarami, a taki ośrodek nazywamy izotropowym. Odpowiednie wektory występujące w poszczególnych równaniach (2-11) są do siebie równoległe.

Gdy parametry ośrodka zależą od kierunku pól, to mówimy o ośrodku anizotropowym, którego własności nie mogą być opisane przez skalarne wielkości $\epsilon ,\mu ,\sigma$. Równania (2-11) mogą być prawdziwe dla ośrodka anizotropowego, ale wtedy parametry materiałowe są reprezentowane przez tensory. Przykładowo, gdy związek między wektorami $E$ i $D$ zależy od kierunku wektora $E$ to przenikalność elektryczna jest tensorem, $[\epsilon ]$, reprezentowanym przez 9-elementową macierz, a relacja między wektorami $D$ i $E$ przybiera postać

$\left[\begin{array}{c}{D}_x\\ D_y\\ D_z\end{array}\right]=\left[\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{xy}& {\epsilon }_{xz}\\ {\epsilon }_{yx}& {\epsilon }_{yy}& {\epsilon }_{yz}\\ {\epsilon }_{zx}& {\epsilon }_{zy}& {\epsilon }_{zz}\end{array}\right]\left[\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right]$  ;

(2-12)

Z powyższego równania wynika, że jedna składowa wektora pola elektrycznego wywołuje, w ogólności, trzy składowe wektora indukcji elektrycznej.

Struktury krystaliczne, np. półprzewodniki, oraz zjonizowane gazy są przykładami anizotropowych dielektryków.

Analogiczną do (2-12) relację można określić dla związku między wektorami $B$ i $H$, w którym przenikalność magnetyczna jest tensorem. W technice mikrofalowej stosuje się ferryty, które są anizotropowymi materiałami magnetycznymi.

• Dielektryki

Materiały dielektryczne powszechnie występują w technice mikrofalowej w konstrukcji tak linii transmisyjnych jak i elementów oraz podzespołów. Rozważmy zachowanie izotropowego dielektryka w zewnętrznym polu elektrycznym o sinusoidalnej zależności od czasu, stosując wektory zespolone.

Pod wpływem pola elektrycznego cząsteczki materii ustawiają się zgodnie z prawem Coulomba tak, że wywołują własne pole elektryczne skierowane przeciwnie do pola zewnętrznego. Zjawisko to określamy mianem elektrycznej polaryzacji (lub krótko polaryzacją) ośrodka i opisujemy przez wektor polaryzacji $P_e$. Wektory $P_e$, $E$ i $D$ powiązane są ze sobą zależnością

$D={\epsilon }_{0}E+P_e$  ;

(2-13)

W ośrodku liniowym, polaryzacja elektryczna jest liniowo związana z zewnętrznym polem elektrycznym jako

$P_e={\epsilon }_0{\chi }_{e}E$  ;

(2-14)

przy czym ${\chi }_e$, która może być zespolona, nazywa się podatnością elektryczną. Tak więc:

$D={\epsilon }_{0}E+P_e={\epsilon }_0(1+{\chi }_e)E=\epsilon E$  ;

(2-15)

gdzie:

$\epsilon ={\epsilon }_0(1+{\chi }_e)={\epsilon }^{\prime }-j{\epsilon }^{″}$  ;

(2-16)

jest zespoloną przenikalnością elektryczną ośrodka.

Zespolony zapis dla przenikalności elektrycznej (2-16) może być stosowany tylko w przypadku pól o sinusoidalnej zależności od czasu.

Przenikalność elektryczną znormalizowaną względem przenikalności elektrycznej próżni nazywamy zespolona względną przenikalnością elektryczną:

${\epsilon }_w=\frac{\epsilon }{{\epsilon }_0}=1+{\chi }_e={\epsilon }^{\prime }-j{\epsilon }_w^{{\text{'}}^{\prime }}$  ;

(2-17)

W przypadku statycznym lub przy wolnych zmianach pola wektor polaryzacji elektrycznej jest w przybliżeniu w fazie z wektorem pola elektrycznego. Dla pól szybkozmiennych opóźnienie wektora $P_e$ względem wektora $E$ nie jest pomijalnie małe, wymienione wektory mają różne fazy. Część urojona $\epsilon$, która opisuje straty w ośrodku (grzanie) wywołane tłumieniem wibracji dipoli i tym samym opóźnienie wektora polaryzacji względem wektora pola elektrycznego, musi być ujemna (${\epsilon }^{″}$ jest dodatnie).

Źródłem strat w dielektryku może być również niezerowa konduktywność ośrodka i wtedy istnieje w ośrodku wektor gęstości prądu przewodzenia opisany zależnością:

$J=\sigma E$  ;

(2-18)

która jest prawem Ohma z punktu widzenia pola elektromagnetycznego.

Całkowita gęstość prądu (przewodzenia i przesunięcia) w dielektryku, która występuje po prawej stronie drugiego równania Maxwella (2-19), wynosi

$\begin{array}{ccc}{J}_C& =& J+j\omega \epsilon E=\sigma E+j\omega ({\epsilon }^{\prime }-j{\epsilon }^{″})E\\ & =& j\omega {\epsilon }^{\prime }E+(\sigma +\omega {\sigma }^{″})E=j\omega [{\epsilon }^{\prime }-j({\epsilon }^{″}+\frac{\sigma }{\omega }\left)\right]E\end{array}$  ;

(2-19)

Z zależności (2-17) wynika, że straty wynikające z tłumienia oscylacji dipoli ($\omega {\epsilon }^{″}$) i straty wynikające z istnienia prądu przewodzenia ($\sigma$) są nierozróżnialne. Wielkość $\sigma +\omega {\epsilon }^{″}$ można traktować jako zastępczą konduktywność ośrodka. Z kolei wielkość ${\epsilon }^{″}+\sigma /\omega$ można określić jako zastępczą część urojoną przenikalności elektrycznej.

Stratność dielektryka możemy charakteryzować przez podanie tangensa kąta stratności wyrażonego wzorem

$tg{\delta }_{\epsilon }=\frac{\sigma +\omega {\epsilon }^{″}}{\omega {\epsilon }^{\prime }}$ ,

(2-20)

który jest stosunkiem składowej prądu będącego w fazie z polem elektrycznym (ten prąd wywołuje straty mocy fali elektromagnetycznej w ośrodku) do składowej prądu proporcjonalnej do $\omega {\epsilon }^{\prime }$, odpowiedzialnej za magazynowanie energii pola elektrycznego.

Zwykle dielektryki charakteryzuje się podając stałą dielektryczną, która jest rzeczywistą częścią względnej przenikalności elektrycznej, oznaczaną w literaturze najczęściej jako ${\epsilon }_w$ (z pominięciem indeksu „’ ”, co może wprawiać w zakłopotanie) oraz tangensa kąta stratności dla określonej częstotliwości.

• Magnetyki

Słownik

• Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
• Mikrofale - zakres częstotliwości fal elektromagnetycznych od 300 MHz do 1000 GHz.
• Równania Maxwella - fundamentalne równania techniki mikrofalowej opisujące pole elektromagnetyczne w czasie i przestrzeni.
• Przenikalność dielektryczna $\epsilon$ i magnetyczna $\mu$ -Podstawowe parametry opisujące właściwości przestrzeni odpowiednio dla pola elektrycznego i magnetycznego.
• Podstawowe parametry pola elektromagnetycznego:
  • Natężenie pola elektrycznego $[V/m]$ .
  • Natężenie pola magnetycznego $[A/m]$ .
• Indukcja pola elektrycznego $D$ - wielkość wektorowa proporcjonalna do natężenia pola elektrycznego i przenikalności dielektrycznej.
• Indukcja pola magnetycznego $B$ - wielkość wektorowa proporcjonalna do natężenia pola magnetycznego i przenikalności magnetycznej.
• I prawo Maxwella - z pierwszego równania Maxwella widać że zmienne pole magnetyczne jest źródłem zmiennego pola elektrycznego
  • W postaci całkowej jest zapisem prawa Faradaya i wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię $S$ z polem elektrycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię (zal. 2-1).
  • W postaci różniczkowej I prawo Maxwella mówi, że rotacja pola elektrycznego jest równa pochodnej indukcji magnetycznej po czasie (zal.2-6).
• II prawo Maxwella - z drugiego równania Maxwella widać że źródłem zmiennego pola magnetycznego jest zmienny w czasie prąd lub zmienne pole elektryczne.
  • W postaci całkowej jest zapisem prawa Ampera i wiąże ze sobą zmianę strumienia indukcji elektrycznej i prąd przenikający powierzchnię $S$ z polem magnetycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię (zal. 2-2).
  • W postaci różniczkowej II prawo Maxwella mówi nam że rotacja pola magnetycznego jest równa pochodnej indukcji elektrycznej i prądu po czasie (zal.2-6).
• III prawo Maxwella - jest zapisem prawa Gaussa dla pola elektrycznego i mówi, że źródłem pola indukcji elektrycznej są ładunki elektryczne.
  • W postaci całkowej prawo to mówi że strumień wektora indukcji pola elektrycznego $D$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ równy jest zgromadzonemu w tej objętości ładunkowi (zal 2-3).
  • W postaci różniczkowej prawo to mówi że divergencja (rozbieżność) wektora indukcji elektrycznej jest równa gęstości ładunku elektrycznego (zal.2-6).
• IV prawo Maxwella - jest zapisem prawa Gaussa dla pola magnetycznego i mówi, że pole magnetyczne jest bezźródłowe.
  • W postaci całkowej prawo to mówi że strumień wektora indukcji pola magnetycznego $B$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ jest równy 0 co znaczy że pole magnetyczne jest bezźródłowe (zal. 2-4).
  • W postaci różniczkowej prawo to mówi, że divergencja (rozbieżność) wektora indukcji magnetycznej jest równa 0, co również znaczy że pola magnetyczne jest bezźródłowe (zal1-6).
• Równanie ciągłości prądu - opisuje relacje między prądem i ładunkiem elektrycznym.
  • W postaci całkowej prawo to mówi nam, że prąd przewodzenia wypływający przez powierzchnię $S$ zamkniętej objętości V równy jest szybkości zmian ładunku w tej objętości (zal.2-5).
  • W postaci różniczkowej prawo to mówi nam, że źródłem pola gęstości prądów jest zmiana gęstości ładunku w czasie (zal 2-6).
• Parametry materiałowe ośrodka dla pola elektromagnetycznego:
  • Przenikalność dielektryczna $\epsilon$ - określa relację między natężeniem pola elektrycznego a jego indukcją (zal. 2-11)
  • Przenikalność magnetyczna $\mu$ - określa relację między natężeniem pola magnetycznego a jego indukcją (zal. 2-11)
  • Konduktywność $\sigma$ - określa relację między natężeniem pola elektrycznego a gęstością prądu przewodzenia ( zal 2-11).
• Rodzaje ośrodków pod katem właściwości dla pola elektromagnetycznego:
  • Ośrodki liniowe i nieliniowe.
  • Ośrodki jednorodne i niejednorodne.
  • Ośrodki dyspersyjne i niedyspersyjne. Parametry materiałowe ośrodka dyspersyjnego zależą a ośrodka niedyspersyjnego nie zależą od częstotliwości.
  • Ośrodki izotropowe i anizotropowe. Parametry materiałowe ośrodka izotropowego nie zależą zaś ośrodka anizotropowego zależą od kierunku pola
• Warunki brzegowe na granicy dwóch dielektryków:
  • Nie ma prądów i ładunków powierzchniowych.
  • Składowe normalne wektorów indukcji $D$ i $B$ oraz składowe styczne wektorów natężenia pól $E$ i $H$ są ciągłe.
• Warunki brzegowe na granicy dielektryk idealny przewodnik: W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości:
  • Pole elektryczne musi być prostopadłe do przewodnika.
  • Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\,\} równej indukcji elektrycznej $D$.
  • Pole magnetyczne musi być styczne do przewodnika.
  • Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej $j$ równej $H$.
• Równania Helmholtza - równania falowe dla pól harmonicznych w zapisie zespolonym.
• Stała propagacji – funkcja parametrów materiałowych ośrodka (zal 2-38). Wartość decyduje o szybkości zmian parametrów fali wzdłuż kierunku propagacji.
• Stała tłumienia część rzeczywista stałej propagacji, decyduje o szybkości strat mocy fali wzdłuż kierunku jej propagacji (zal. 2-51a)
• Stała fazowa część urojona stałej propagacji, decyduje o szybkości zmian fazy fali ( zal. 2-51b, 2-52b).
• Prędkość fazowa fali - prędkość z jaką przesuwa się płaszczyzna stałej fazy fali.
• Prędkość grupowa fali - jest prędkością przepływu energii.
• Fala płaska - Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Powierzchnia ekwifazowa fali płaskiej jest płaszczyzna prostopadłą do kierunku propagacji.
• Właściwości fali płaskiej - fala płaska jest falą typu TEM (Transverse Electro-Magnetic)
  • Wektory $E$ i $H$ fali TEM leżą w płaszczyźnie prostopadłej do kierunku propagacji i są prostopadłe względem siebie.
  • Zwrot iloczynu wektorowego pola $E$ razy pole $H$ wyznacza kierunek propagacji a jego moduł gęstość mocy fali.
  • Impedancja falowa (stosunek wartości wzajemnie prostopadłych składowych pola $E$ i $H$) fali płaskiej jest równy impedancji właściwej ośrodka.

---

Bibliografia

1. Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
2. Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
3. Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
4. Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.

---