|
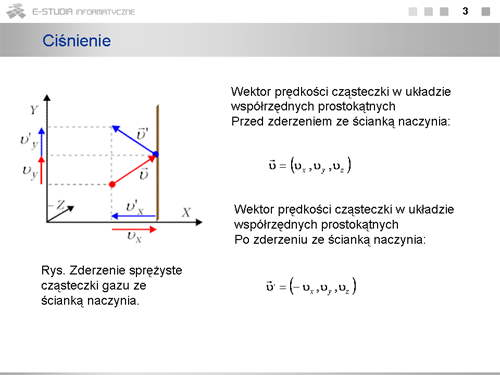
W układzie współrzędnych prostokątnych rozważamy sprężyste zderzenie cząsteczki gazu, o wektorze prędkości , ze ścianką naczynia prostopadłą do osi . Prędkość cząsteczki zapiszemy w postaci wektora
Po odbiciu się od ścianki naczynia cząsteczka porusza się z prędkością . W wyniku sprężystego zderzenia cząsteczki ze ścianką prostopadłą do osi zmieni znak tylko składowa prędkości wzdłuż tej osi, czyli będzie
- , ,
Dalsze nasze rozważania dotyczyć będą tylko kierunku , stosować będziemy zapis skalarny.
|