TTS Moduł 8

Głównymi celami Wykładu 8 jest zapoznanie studiującego z tak ważnymi narzędziami techniki mikrofalowej, jak: wytwarzanie drgań harmonicznych o sinusoidalnym przebiegu i o kontrolowanej amplitudzie i częstotliwości, modulacja i demodulacja sygnałów, detekcja, przemiana częstotliwości.

---

Materiał obu części Wykładu jest obszerny i zapoznaje on studiującego z wieloma nowymi zagadnieniami, technikami i z wielką liczbą nowych pojęć.

---

Na rysunku obok widzimy obraz sygnału o częstotliwości 100MHz otrzymany na ekranie analizatora widma. Sygnał poddany został modulacji amplitudy, a świadczą o tym dwie wstęgi boczne oddalone od prążka fali nośnej o 10 kHz. Jak skonstruowany jest oscylator mikrofalowy, jak go zaprojektować, aby uzyskać sygnał „czysty” w sensie widmowym? Jak skonstruować mechanizm przestrajania i modulacji częstotliwości generatora? Jak przeprowadzić proces modulacji przed wysłaniem sygnału w eter? Jak odzyskać informację po odbiorze sygnału? Oto seria pytań, na które Czytelnik znajdzie odpowiedź w tym wykładzie.

---

O generatorze i warunkach generacji można mówić na kilka sposób, gdyż opracowano wiele modeli opisujących pracę generatora. Jednym z najpopularniejszych jest model dwójnikowy. Na rysunku pokazano ideową strukturę oscylatora, zawierającą trzy podstawowe składniki: element aktywny (np. tranzystor...) umożliwiający powstanie oscylacji, obwód strojenia z rezonatorem, który decyduje o częstotliwości generacji, obciążenie, odbierające wytworzony sygnał. Między rezonatorem a elementem aktywnym a rezonatorem wybrano parę zacisków. W stanie ustalonym sinusoidalnych oscylacji między zaciskami panuje napięcie o amplitudzie zespolonej $U$, oraz płyną prądy o zespolonych amplitudach $I_a$ – w stronę obwodu aktywnego - i $I_c$ w stronę rezonatora. Wymienione prądy łączy oczywisty związek. Na jego podstawie można zdefiniować dwie admitancje: obwodu aktywnego $Y_a$ i obwodu strojenia z rezonatorem $Y_C$ – patrz rysunek. Prowadzi to do admitancyjnego warunku generacji. W powyższym wywodzie pominięto wpływ harmonicznych sygnału generowanego.

---

Analiza bilansu mocy w obwodzie generatora wymaga wprowadzenia pojęcia mocy ujemnej. Moc $P_c$ absorbowana przez rezonator i obciążenie jest dodatnia, jest to moc tracona. Moc $P_a$ jest ujemna, gdy konduktancja Moc $G_a$ jest ujemna. Oznacza to, że konduktancja $G_a$ „pompuje” moc prądu zmiennego do obwodu zewnętrznego. Warunek bilansu mocy jest spełniony w stanie ustalonym generacji. Jednak w stanie narastania lub gaśnięcie oscylacji suma mocy $P_a+P_C$ jest różne od zera. Aby wyjaśnić ten fakt wygodnie jest przyjąć, że prąd $I_c$ jest w fazie z $U$, co oznacza, że prąd $I_a$ jest przesunięty o $180^{\circ }$ względem $U$. Element aktywny, np. tranzystor, jest nieliniowy, co oznacza, że prąd $|I_a|$ tylko do pewnej granicy jest proporcjonalne do $|U_a|$ . W rezultacie moc $P_a$ jest proporcjonalna do $|U{|}^2$ jedynie dla małych amplitud i przechodzi ze wzrostem $|U|$ przez swoje maksimum. 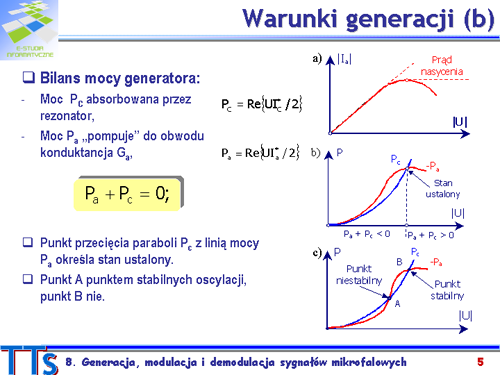Obwód strojenia jako bierny nie wykazuje nieliniowości i wykres $P_C(|U|)$ jest parabolą. Na rysunku b) pokazano wykresy obu mocy. Punkt przecięcia paraboli $P_C$ z linią mocy $P_a$ określa stan ustalony, w którym spełniony jest bilans mocy. Generację inicjują szumy elementu aktywnego. Dla małych amplitud moc dostarczana przez obwód aktywny przewyższa moc traconą, gdyż $P_a+P_c<0$. Nadwyżka mocy powoduje, że amplituda drgań narasta, wzrasta energia zgromadzona w polu elektromagnetycznym obwodu rezonansowego. Proces narastania amplitudy trwa tak długo, aż spełniony zostanie bilans mocy. Gdy $P_a+P_c<0$ , drgania gasną. Na rysunku c) pokazano inny, typowy dla generatora obcowzbudnego, przebieg mocy $P_a$. Proces samowzbudzenia nie nastąpi, ponieważ dla małych napięć bilans mocy jest niekorzystny, moc tracona przewyższa moc oddaną przez obwód aktywny. Doprowadzenie mocy z zewnątrz może wprowadzić obwód w stan, gdzie $P_a+P_c<0$. Powstaje pytanie, który z punktów przecięcia charakterystyk, A czy B będzie punktem stabilnych oscylacji. Łatwo zauważyć, że będzie nim punkt B, w którym jest spełniony warunek:

---

Przeanalizujemy dokładniej admitancyjny warunek generacji. Admitancja $Y_a$ zależy od wielu zmiennych: warunków polaryzacji elementu aktywnego $(U_0,I_0)$ , częstotliwości $f$ i amplitudy sygnału oscylacji $|U|$. Dla małych sygnałów $Y_a=Y_{a0}$. Admitancja obwodowa $Y_c$ jest sumą 2 składników: admitancji rezonatora $Y_r$ i admitancji obciążenia $Y_L$ – patrz rysunek. Dla uproszczenia przyjmiemy założenie, że $Y_L$ jest czysto rzeczywiste. Admitancja rezonatora $Y_r$ jest silnie zależna od częstotliwości. Warunek admitancyjny generacji można teraz zapisać jako dwa oddzielne warunki: amplitudy i fazy. Na rysunku pokazano graficzną interpretację admitancyjnego warunku generacji. Linia niebieska to admitancja obwodowa, silnie zależna od częstotliwości, Linia czerwona opisuje zachowanie admitancji obwodu aktywnego. Ze wzrostem amplitudy wartość $Y_a$ zmienia się od $Y_{a0}$ do wartości odpowiadającej punktowi przecięcia. Tak więc położenie punktu przecięcia na linii $Y_a$ określa amplitudę oscylacji, a na linii $Y_C$ częstotliwość oscylacji.

---

Oscylator można przedstawić w ogólnej postaci obwodu zastępczego z rysunku a). Wybieramy wrota w prowadnicy łączącej obwód strojenia z obwodem aktywnym. W ustalonym stanie generacji rozchodzą się fale o amplitudach $U_i$ i $U_r$. W tej wybranej płaszczyźnie określane są ${\mathrm{\Gamma }}_a$ współczynnik odbicia obwodu aktywnego i ${\mathrm{\Gamma }}_c$ współczynnik odbicia obwodu strojenia: Reflektancyjny warunek generacji jest zapisem oczywistego faktu, że jeden współczynnik jest odwrotnością drugiego: Oznaczymy moduły i argumenty obu współczynników odbicia: dla obwodu aktywnego ${\mathrm{\Gamma }}_a=|{\mathrm{\Gamma }}_a|e^{j{\gamma }_a}$ i dla obwodu strojenia ${\mathrm{\Gamma }}_c=|{\mathrm{\Gamma }}_c|e^{j{\gamma }_c}$ . Warunek generacji można zapisać dwoma równościami: warunkiem amplitudy, oraz warunkiem fazy. Współczynnik odbicia obwodu aktywnego ${\mathrm{\Gamma }}_a={\mathrm{\Gamma }}_{a0}(U_0,I_0,\omega )S(|U_r|)$ jest funkcją kilku zmiennych, podobnie jak admitancja $Y_a$. Natomiast współczynnik odbicia obwodu strojenia ${\mathrm{\Gamma }}_S(\omega )$ jest funkcją częstotliwości. Ilustracja warunku generacji na płaszczyźnie zespolonej wymaga wykreślenia zależności ${\mathrm{\Gamma }}_S(\omega )$ i odwrotności $1/{\mathrm{\Gamma }}_a(P)$, co pokazano na rysunku b). Punkt przecięcia wskazuje stan ustalony generacji. Położenie tego punktu na linii ${\mathrm{\Gamma }}_S(\omega )$ wyznacza częstotliwość oscylacji, a na linii $1/{\mathrm{\Gamma }}_a(P)$ wyznacza moc oscylacji.