PF Moduł 16

---

Wstęp Falowa natura światła była znana znacznie wcześniej niż odkryto, że jest ono falą elektromagnetyczną. Świadczyły o tym typowe zjawiska falowe, takie jak interferencja, czyli nakładanie się fal, czy dyfrakcja, czyli ugięcie na szczelinie. Warunkiem powstania trwałego obrazu interferencyjnego jest spójność światła, czyli niezmienna w czasie różnica faz między nakładającymi się falami. Naturalne źródła światła emitują światło niespójne, o przypadkowo zmieniającej się fazie. Z tego powodu nie możemy zaobserwować na ścianie wzmocnień i wygaszeń światła pochodzącego na przykład od dwóch żarówek. Takie wzmocnienia i wygaszenia wprawdzie powstają, ale ich położenia chaotycznie i szybko się zmieniają tak, że nasze oko rejestruje tylko jednolicie oświetloną płaszczyznę. Warunek spójności będzie spełniony, jeśli światło rozdzieli się, na przykład, podczas przejścia przez układ szczelin. Wtedy każda szczelina zgodnie zasadą Huyghensa będzie źródłem światła i będzie to światło spójne. W module tym omówimy zjawiska interferencji i dyfrakcji, a także efekty wynikające ze złożenia tych dwóch zjawisk. Pokażemy, jak opisane efekty można wykorzystać w siatce dyfrakcyjnej, a także do badania sieci krystalicznej przez wywołanie zjawiska dyfrakcji promieniowania rentgenowskiego na krysztale. Omówione zostanie również zjawisko Dopplera, dobrze każdemu znane z obserwacji dźwięków towarzyszących ruchowi ulicznemu.

---

Interferencja światła Doświadczenie Younga Z zasady superpozycji fal wynika, że jeśli dwie fale przemieszczają się w tym samym ośrodku, to powodowane przez nie zaburzenia w danym punkcie przestrzeni nakładają się, to znaczy, dodają lub odejmują się w zależności od tego, czy są tego samego czy różnego znaku. Zjawiska związane z nakładaniem się fal noszą nawę interferencji. Zjawisko interferencji dla fal świetlnych zostało po raz pierwszy zaobserwowane i zinterpretowane jako przejaw falowej natury światła przez Thomasa Younga w 1801 roku. Uproszczony schemat doświadczenia Younga przedstawia rysunek. Światło w postaci fali płaskiej pada na układ dwóch szczelin $S_1$ i $S_2$ w przesłonie $P$. Interesuje nas rezultat nałożenia się fal w punkcie $A$ na ekranie $E$ ustawionym za szczelinami. Światło padające symbolizują równoległe niebieskie linie (powierzchnie falowe) i strzałki (promienie) z lewej strony. Promienie świetlne, które przeszły przez szczeliny $S_1$ i $S_2$ docierają do punktu $A$, ale drogi ich $r_1$ i $r_2$ nie są takie same. Jeśli więc faza fali świetlnej była w płaszczyźnie szczelin taka sama, to w punkcie $A$ będzie różna wskutek różnicy dróg. Warunek wzmocnienia lub wygaszenia wynika z geometrycznych zależności zilustrowanych na rysunku. Trzeba tu zwrócić uwagę, że w rzeczywistości odległość ekranu od przesłony jest o wiele większa niż odległość pomiędzy szczelinami tzn. $H>>d$ . W takim przypadku promienie $r_1$ i $r_2$ są z dobrym przybliżeniem równoległe, a trójkąty $SBA$ i $S_{1}a{S}_2$ możemy uznać za podobne, co z kolei oznacza, że kąty $ASB$ i $S_2{S}_{1}a$ są sobie równe. Kąt $ASB$, który może być łatwo zmierzony, oznaczyliśmy symbolem $\theta$. Różnica dróg promieni od szczelin do punktu $A$ równa jest $dsin\theta$. Jeśli różnica ta będzie równa całkowitej wielokrotności długości fali, to nastąpi wzmocnienie, jeśli równa będzie równa nieparzystej wielokrotności połowy długości fali - nastąpi wygaszenie. Warunek uzyskania maksimum natężenia fali wypadkowej zapiszemy w postaci: $dsin\theta =n\lambda$ , warunek uzyskania minimum, czyli wygaszenia: $dsin\theta =(2n+1)\frac{\lambda }{2}=(n+\frac{1}{2})\lambda$

---

Z postaci wzorów widzimy, że im mniejsza jest odległość pomiędzy szczelinami tym większa będzie wartość kąta, dla którego wystąpi wzmocnienie (lub wygaszenie) i tym większa będzie różnica kątowa pomiędzy maksimami bądź minimami. Rysunek przedstawia ilustrację interferencji w doświadczeniu Younga dla dwóch różnych odległości pomiędzy szczelinami; z lewej - mniejszej, z prawej - większej.

---

Uogólnijmy nasze rozważania. Rozpatrzmy dwie fale o tych samych amplitudach i częstościach, ale różniące się fazą: $y_1=y_{0}sin(kx-\omega t)$ oraz $y_1=y_{0}sin(kx-\omega t-\phi )$. Jak wspominaliśmy już, w przypadku fal elektromagnetycznych, jako zaburzenie y traktujemy zazwyczaj wartość wektora natężenia pola elektrycznego. Zgodnie z zasadą superpozycji fal, zaburzenie wypadkowe w danym punkcie przestrzeni i momencie czasu będzie sumą zaburzeń pochodzących od obu fal $y_{12}=y_1+y_2$. Po zastosowaniu trygonometrycznego wzoru na sumę sinusów, otrzymujemy: $y_{12}=y_0[2sin(kx-\omega t-\phi )cos\frac{\phi }{2}]$

---

We wzorze na $y_{12}$ możemy wyodrębnić czynnik niezależny od czasu i położenia. Jest to amplituda równa $2y_{0}cos\frac{\phi }{2}$. Amplituda ta zależy od $\phi$, czyli różnicy faz pomiędzy falami. Maksymalna amplituda równa będzie podwojonej amplitudzie fal składowych, co nastąpi, kiedy różnica faz będzie równa zeru. Amplituda równa zeru będzie dla różnicy faz równej $\pi$, wtedy przeciwne w fazie zaburzenia będą się wzajemnie znosić. Dla innych różnic faz amplituda będzie przyjmować wartości pośrednie.

---

Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej.

---

Na zakończenie dwie uwagi: W praktyce, dla spełnienia zarówno warunków równoległości promieni jak i skończonej odległości $H$ pomiędzy przesłoną i ekranem, stosuje się zwykle soczewkę skupiającą równoległe promienie w płaszczyźnie ogniskowej, gdzie umieszcza się ekran; Założyliśmy tu milcząco, że szerokość szczeliny jest zaniedbywanie mała w stosunku do odległości pomiędzy szczelinami. Przypadek ogólny, kiedy obie te wielkości są porównywalne, rozpatrzymy w następnej części tej lekcji omawiając zjawiska dyfrakcji.

---

Czy możliwa jest interferencja światła przechodzącego przez pojedynczą szczelinę lub otwór? Odruchowa odpowiedź jest - że nie, bo przechodzące światło nie ma z czym interferować. Zasada Hyghensa mówi jednak, że każdy punkt, do którego dochodzi fala staje się źródłem nowej fali kulistej. Fale pochodzące z różnych punktów szczeliny mogą więc także interferować. Kiedy szczelina jest bardzo szeroka, to w rezultacie tworzy się czoło fali płaskiej i efektu interferencji nie obserwujemy. Kiedy jednak rozmiary szczeliny stają się porównywalne z długością fali, efekt interferencji powinien być możliwy do zaobserwowania. Rzeczywiście, efekty takie się obserwuje i choć w swej naturze nie różnią się one od znanej nam już interferencji otrzymały inną nazwę - dyfrakcji, czyli "uginania się" fal. Na rysunku pokazano dwa przykładowe promienie, które będą z sobą interferować. Szerokość szczeliny oznaczamy symbolem $h$. Podobnie jak poprzednio, zakładamy, że $H>>h$ i możemy uznać promienie biegnące z różnych punktów szczeliny za równoległe, co jest na ogół z niezłym przybliżeniem spełnione i upraszcza opis ilościowy. Taki przypadek nosi nazwę dyfrakcji Fraunhofera w odróżnieniu od dyfrakcji Fresnela, gdzie zakłada się, że odległość pomiędzy źródłem i ekranem ma skończoną wartość. Rozważmy na początek dwa promienie wybiegające z punktów szczeliny odległych o $h/2$. Warunek ich wygaszania się $\frac{h}{2}sin\theta =(n+\frac{1}{2})\lambda$ dla n=0 (pierwsze minimum) wyraża się wzorem: Parser nie mógł rozpoznać (błąd składni): {\displaystyle \frac{h}{2}sin\theta=\frac{1}{2} \right)\lambda}

---

Na poprzednim rysunku rozważaliśmy jeden promień z górnego krańca szczeliny, drugi z jej środka. Możemy jednak przemieszczać się w dół z położeniami obu promieni odnajdując dla każdego promienia z górnej połowy szczeliny odpowiadający mu promień z połowy dolnej. Warunek na wygaszenie będzie dla tych przesuniętych promieni identyczny jak poprzednio.

---

Możliwe są i inne kombinacje. Gdyby odległość pomiędzy rozważanymi promieniami była równa jednej czwartej szerokości szczeliny, to warunek na wygaszanie byłby: Parser nie mógł rozpoznać (błąd składni): {\displaystyle \frac{1}{4}h sin\theta=\frac{1}{2} \right)\lambda} , czyli $hsin\theta =2\lambda$ Uogólniając, można napisać, że warunek na wygaszanie się promieni biegnących z różnych punktów szczeliny ma postać: $hsin\theta =n\lambda$ , gdzie $n=1,2,3,...$

---

Minimów i leżących pomiędzy nimi maksimów może więc być bardzo wiele. Powstaje pytanie, jaki będzie rozkład natężeń w obrazie dyfrakcyjnym, jak natężenie wypadkowej fali zależeć będzie od kąta odchylenia promieni od pierwotnego kierunku? Największe wzmocnienie natężenia fali uzyskujemy, gdy obie fale mają taką sama fazę, największe osłabienie, gdy faza jest przeciwna. Pomiędzy tymi skrajnymi przypadkami mamy wszystkie przypadki pośrednie, zależne od różnicy faz. Podzielmy w myśli całą szerokość szczeliny na n pasków. Ilustruje to rysunek obok, gdzie $n=5$. (Wskaźnik $n$ odgrywa tu pomocniczą rolę i nie należy go mylić ani ze współczynnikiem załamania, ani z numeracją maksimów i minimów interferencyjnych.) Różnica faz $\mathrm{\Delta }\phi$ dla fal biegnących od dwóch sąsiednich pasków zależy od różnicy dróg $\mathrm{\Delta }r$, jak pokazano na rysunku. Kiedy różnica dróg równa jest długości fali, to odpowiadająca różnica faz równa jest $2\pi$. Mamy więc proporcję: $\frac{\mathrm{\Delta }r}{\lambda }=\frac{\mathrm{\Delta }\phi }{2\pi }$ czyli $\mathrm{\Delta }\phi =\frac{2\pi }{\lambda }\mathrm{\Delta }r=\frac{2\pi }{\lambda }\mathrm{\Delta }hsin\theta$ gdzie $\mathrm{\Delta }h$ jest odległością pomiędzy punktami w płaszczyźnie przesłony, to jest szerokością myślowo wyodrębnionego jednego paska. Otrzymaliśmy wzór na różnicę fazy między falami pochodzącymi od kolejnych części szczeliny. Musimy teraz dodać wszystkie fale, aby znaleźć falę wypadkową, czyli jej amplitudę i fazę.

---

Dla wyznaczenia sumarycznej fazy oraz amplitudy wypadkowej fali wykorzystamy tu metodę tak zwanych strzałek fazowych. Metoda ta umożliwia graficzne dodawanie wielkiej liczby fal o tej samej amplitudzie $E_0$ i częstości $\omega$, a różniących się fazą. Ilustruje to rysunek. Niech pierwsza fala wynosi $E_1=E_{0}sin(\omega t)$ , kolejna - różniąca się od pierwszej przesunięciem w fazie o $\phi$ będzie $E_2=E_{0}sin(\omega t+\phi )$, kolejna niech będzie przesunięta o $2\phi$ itd. Każda strzałka reprezentuje falę o danej amplitudzie, której odpowiada długość strzałki. Faza fali określona jest przez kąt między osią x a kierunkiem strzałki. Wypadkową amplitudę i fazę otrzymujemy sumując wektorowo strzałki (kolejna strzałka ma swój początek w miejscu, gdzie kończy się poprzednia). Na rysunku pokazane są przykładowo różnymi kolorami cztery fale i ich złożenie pokazane kolorem czerwonym.

---

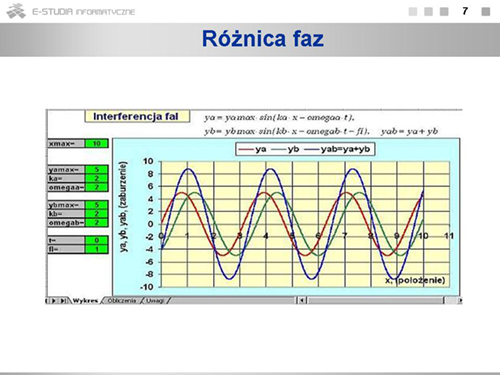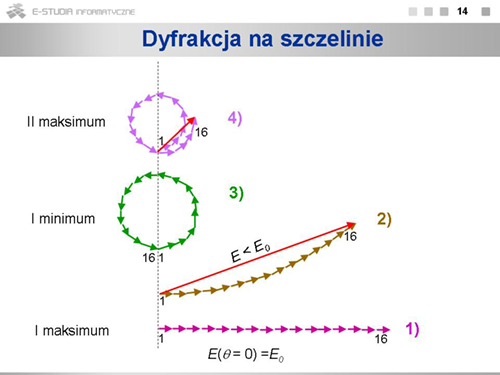
W naszym przypadku fali przechodzącej przez szczelinę, sumaryczna amplituda i sumaryczna faza będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem $\mathrm{\Delta }\phi =\frac{2\pi }{\lambda }\mathrm{\Delta }hsin\theta$ od kąta $\theta$ określającego położenie danego punktu na ekranie względem szczeliny. Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i $\mathrm{\Delta }\phi$ będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą $n$ jednakowych składników. Jeśli kąt $\theta$ będzie inny, musimy sumować $n$ fal składowych zgodnie z metodą strzałek fazowych. Ilustruje to rysunek, gdzie $n=16$. Przypadek 1) odpowiada sytuacji, gdy $\theta =0$, a więc i różnica faz $\mathrm{\Delta }\phi =0$. Sumaryczna amplituda jest tu maksymalna, oznaczyliśmy ją $E_0$. Kolejne przypadki 2), 3) i 4) odpowiadają wzrastającej wartości kąta obserwacji $\theta$. Przypadek 2) ilustruje sytuację, gdy $\theta$ nieco większe od zera. Suma algebraiczna wszystkich 16 składników (długość łuku) jest taka sama, jak poprzednio, równa $E_0$, ale wypadkowa amplituda (wartość sumy wektorowej) jest mniejsza od $E_0$. W przypadku 3) sumaryczna amplituda wynosi zero, czyli będzie to pierwsze minimum. Przy dalszym wzroście kąta $\theta$ amplituda znów będzie różna od zera, ale jej wartość stanie się o wiele mniejsza. Liczba pasków, na które podzieliliśmy w myśli szczelinę może być dowolna. Im będzie większa, tym węższe będą paski, ale końcowe przesunięcie fazowe i zmiana amplitudy będą, dla danej długości fali, określone tylko wartością kąta odchylenia $\theta$. (Pomocniczy wskaźnik $n$ przestaje więc być istotny i dalej potrzebny.) Związek pomiędzy wartością kąta $\theta$, a amplitudą wypadkowej fali możemy znaleźć rozpatrując zależności geometryczne zilustrowane na rysunku.

---

Kiedy liczba pasków będzie zmierzać do nieskończoności, a ich szerokość do zera, to łuk strzałek fazowych będzie można przybliżyć łukiem okręgu. Długość łuku jest równa $E_0$, a kąt $\phi$ pomiędzy stycznymi do łuku na obu jego końcach równy jest różnicy faz pomiędzy promieniami biegnącymi z obu krańców szczeliny. Kąt ten, mierzony w radianach, równy jest z definicji stosunkowi długości łuku, czyli $E_0$, do promienia $R$ to znaczy $\phi =E_0/R$. Z kolei, jak widać na rysunku, wypadkowa amplituda fali obserwowanej pod kątem $\theta$ wynosi $E_{\theta }=2Rsin\alpha$ , zaś $\alpha =\phi /2$ . Wynika z tego, że $E_{\theta }=E_0\frac{sin\alpha }{\alpha }$. Wypadkowa różnica faz odpowiada promieniom biegnącym z dwóch krańców szczeliny i określona jest tak samo, jak różnica faz dla dwóch sąsiednich pasków, jeśli szerokość paska zamienimy szerokością szczeliny: $\phi =\frac{2\pi }{\lambda }hsin\theta =2\alpha$ , czyli $\alpha =\frac{\pi }{\lambda }hsin\theta$ . W ten sposób różnica faz $\phi$ określona została przez mierzalne wielkości: szerokość szczeliny $h$, długość fali $\lambda$ i kąt obserwacji $\theta$. Podstawiając wyznaczoną wypadkową różnicę faz do wzoru $E_{\theta }=E_0\frac{sin\alpha }{\alpha }$ , otrzymujemy wyrażenie na amplitudę fali wypadkowej. Intensywność obrazu dyfrakcyjnego proporcjonalna jest do kwadratu amplitudy. Zapiszmy więc kompletny wzór na rozkład intensywności obrazu dyfrakcyjnego zależny jedynie od mierzalnych wielkości, czyli umożliwiający weryfikację doświadczalną. Przez $I_{wzgl}$ oznaczamy względną intensywność określoną jako stosunek intensywności dla danego kąta do intensywności maksymalnej, czyli dla kąta $\theta$ równego zeru. $I_{\theta }=I_0{\left(\frac{sin\alpha }{\alpha }\right)}^2$ , lub $I_{wzgl}=\frac{I_{\theta }}{I_0}={\left(\frac{sin\alpha }{\alpha }\right)}^2$ , gdzie $\alpha =\pi \left(\frac{h}{\lambda }\right)sin\theta$

---

Warto zobaczyć, jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru na $I_{wzgl}$ widać, że zależy nie tyle od samych tych wartości, ale od ich stosunku $h/\lambda$ . Szerokość głównego maksimum dyfrakcyjnego jest tym większa, im węższa jest szczelina. Gdy szerokość szczeliny jest dużo większa od długości fali (dolny wykres) zjawiska dyfrakcji, czyli ugięcia na szczelinie, praktycznie nie obserwujemy.

---

Złożenie interferencji i dyfrakcji Uzyskaliśmy interferencyjne efekty na pojedynczej szczelinie, zaś poprzednio rozważaliśmy układ dwóch szczelin, gdzie również określiliśmy warunki na wzmacnianie i wygaszanie wypadkowej fali interferencyjnej. Można się więc spodziewać, że w układzie dwóch szczelin, uzyskamy superpozycje obu dyskutowanych tu efektów. Przypomnijmy sobie wzór na falę, będącą rezultatem nałożenia się dwóch fal o tych samych częstościach i amplitudach. Uzyskujemy fale wypadkową, $y_{12}$, której amplituda zależy od różnicy faz fal składowych. W naszym przypadku możemy wzór na amplitudę zapisać następująco: $E_i=2E_{0i}cos\left(\frac{{\phi }_i}{2}\right)=E_{m}cos{\alpha }_i$ gdzie przez $E_i$ (i – od interferencji) oznaczyliśmy amplitudę fali zależną od różnicy faz promieni przechodzących przez dwie szczeliny, a przez $E_{0i}$ amplitudę fali biegnącej z każdej szczeliny. Amplituda maksymalna $E_m$ jest sumą obu amplitud składowych $E_m=2E_{0i}$. Podobnie jak w przypadku dyfrakcji ${\alpha }_i={\phi }_i/2$. Należy jeszcze powiązać różnicę faz z kątem odchylenia promieni od pierwotnego kierunku fali padającej na układ szczelin. Wykorzystamy tu otrzymaną dla pojedynczej szczeliny zależność $\alpha =\frac{\pi }{\lambda }hsin\theta$ , gdzie zamiast szerokości szczeliny h wstawiamy odległość pomiędzy dwoma szczelinami $d$ : ${\alpha }_i\frac{\pi d}{\lambda }sin\theta$. Natężenie fali (intensywność) jest proporcjonalna do kwadratu amplitudy. Intensywność obrazu interferencyjnego możemy więc zapisać w postaci: $I_i=I_{mi}co{s}^2{\alpha }_i$ gdzie $I_{mi}$ jest maksymalną intensywnością promieni biegnących z każdej szczeliny.

---

Ta maksymalna intensywność zależna jest jednak od efektów dyfrakcyjnych $I_{mi}=I_0{\left(\frac{sin\alpha }{\alpha }\right)}^2$. Intensywność łączna zawierająca w sobie oba efekty wyrazi się więc wzorem: $I_{{\theta }_{id}}=I_m(cos{\alpha }_i{)}^2\cdot {\left(\frac{sin{\alpha }_d}{{\alpha }_d}\right)}^2$ , gdzie ${\alpha }_i=\frac{\pi d}{\lambda }sin\theta$ , ${\alpha }_d=\frac{\pi h}{\lambda }sin\theta$ Jest to końcowy wzór zależny wyłącznie od wielkości mierzalnych. Indeksami "i" i "d" oznaczyliśmy kąty odpowiadające interferencji i dyfrakcji. Symbolem d oznaczona jest odległość pomiędzy szczelinami, a symbolem h, szerokość każdej ze szczelin. $I_m$ jest maksymalną intensywnością odpowiadającą promieniom biegnącym na wprost.

---

Obraz interferencyjno - dyfrakcyjny określony powyższym wzorem pokazany jest na rysunku. Widzimy tu szereg maksimów interferencyjnych (fioletowa linia), których intensywność określona jest przez efekty dyfrakcyjne (czerwona linia). Dolny wykres odpowiada trzy razy mniejszej odległości między szczelinami d niż górny. Zmniejszenie odległości wpłynęło na poszerzenie linii.

---

Szerokość szczelin $h$ wpływa natomiast na zależność intensywności linii od kąta odchylenia $\theta$. Dla szerokich szczelin intensywność szybko maleje wraz z kątem $\theta$, dla szczelin wąskich możemy obserwować stosunkowo silne linie przy dużych kątach odchylenia.

---

Siatką dyfrakcyjną nazywamy układ wielu szczelin. Charakteryzuje ją wielkość zwana stałą siatki $d$, która równa jest odległości pomiędzy dwiema sąsiednimi szczelinami, szerokość szczeliny $h$ oraz liczba szczelin $N$. Oczekujemy, że w przypadku siatki dyfrakcyjnej efekt interferencyjny będzie silniejszy, bo sumować się będą składniki pochodzące od każdej pary sąsiednich szczelin. Wystąpią też efekty dodatkowe związane z interferencją pomiędzy innymi kombinacjami dwóch szczelin w siatce. Warunek wzmocnienia dla par sąsiednich szczelin będzie taki sam jak dla układu dwóch szczelin, czyli kąt odchylenia określony będzie stosunkiem długości fali padającej do stałej siatki. Podobnie jak w przypadku dwóch szczelin o określonych szerokościach wystąpią też efekty dyfrakcyjne zależne od szerokości samych szczelin $h$. Zapiszmy więc warunek wzmocnienia w postaci: $sin\theta =n\frac{\lambda }{d}$ , gdzie $n=1,2,3,...$ Wielkość $n$ nazywamy rzędem widma.