PEE Zadania egzaminacyjne: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 7: | Linia 7: | ||
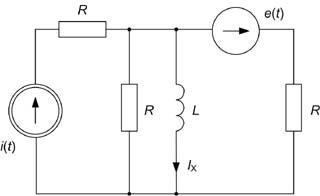
Obliczyć prąd <math>I_x\,</math> w obwodzie metodą Thevenina | Obliczyć prąd <math>I_x\,</math> w obwodzie metodą Thevenina | ||
[[Grafika: | [[Grafika:PEE_Zadania_egz_zes1_1.jpg]] | ||
Dane: <math>i(t)=5\sqrt{2}sin(\omega t+90^\circ)\, A</math>, <math>e(t)=10\sqrt{2}sin(\omega t-90^\circ)\, V</math>, <math>R=50\Omega</math>, <math>\omega L=3\Omega</math> | Dane: <math>i(t)=5\sqrt{2}sin(\omega t+90^\circ)\, A</math>, <math>e(t)=10\sqrt{2}sin(\omega t-90^\circ)\, V</math>, <math>R=50\Omega</math>, <math>\omega L=3\Omega</math> | ||
| Linia 17: | Linia 17: | ||
Obliczyć przebieg <math>u_C(t)</math> w stanie nieustalonym po przełączeniu w obwodzie | Obliczyć przebieg <math>u_C(t)</math> w stanie nieustalonym po przełączeniu w obwodzie | ||
[[Grafika: | [[Grafika:PEE_Zadania_egz_zes1_2.jpg]] | ||
Dane: <math>e_1(t)=50V\,</math>, <math>e_2(t)=60\sqrt{2}sin(\omega t+90^\circ)\, V</math>, <math>R=10\Omega</math>, <math>C=0,1F\,</math> | Dane: <math>e_1(t)=50V\,</math>, <math>e_2(t)=60\sqrt{2}sin(\omega t+90^\circ)\, V</math>, <math>R=10\Omega</math>, <math>C=0,1F\,</math> | ||
| Linia 27: | Linia 27: | ||
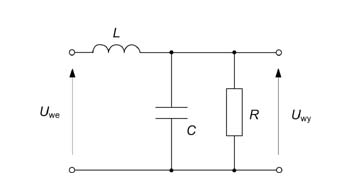
Określić transmitancję napięciową, odpowiedź impulsową i charakterystyki częstotliwościowe | Określić transmitancję napięciową, odpowiedź impulsową i charakterystyki częstotliwościowe | ||
[[Grafika: | [[Grafika:PEE_Zadania_egz_zes1_3.jpg]] | ||
Dane: <math>R=50\Omega</math>, <math>L=1H\,</math>, <math>C=0,5F\,</math> | Dane: <math>R=50\Omega</math>, <math>L=1H\,</math>, <math>C=0,5F\,</math> | ||
<hr width="100%"> | |||
'''Zestaw 2''' | |||
Zad. 1 | |||
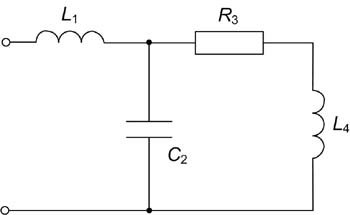
Narysować wykres wektorowy dla obwodu | |||
[[Grafika:PEE_Zadania_egz_zes2_1.jpg]] | |||
<hr width="100%"> | |||
Zad. 2 | |||
Obliczyć moce elementów w obwodzie i sporządzić bilans mocy. | |||
[[Grafika:PEE_Zadania_egz_zes2_1.jpg]] | |||
Dane: <math>X_{L1}=\omega L_1=40\Omega</math>, <math>X_{L2}=\omega L_2=20\Omega</math>, <math>X_M=\omega M=20\Omega</math>, <math>R=40\Omega</math>, <math>|U_f|=100V\, </math> | |||
<hr width="100%"> | |||
Zad. 3 | |||
Obliczyć przebieg <math>u_C(t)</math> w stanie nieustalonym po przełączeniu w obwodzie | |||
[[Grafika:PEE_Zadania_egz_zes2_3.jpg]] | |||
Dane: <math>R_1=30\Omega</math>, <math>R_2=20\Omega</math>, <math>C=0,01F\,</math>, <math>e_1(t)=200V\,</math>, <math>e_2(t)=15V\,</math>, | |||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 22:18, 2 sie 2006
Zadania egzaminacyjne
Zestaw 1
Zad. 1
Obliczyć prąd w obwodzie metodą Thevenina
Dane: , , ,
Zad. 2
Obliczyć przebieg w stanie nieustalonym po przełączeniu w obwodzie
Dane: , , ,
Zad. 3
Określić transmitancję napięciową, odpowiedź impulsową i charakterystyki częstotliwościowe
Dane: , ,
Zestaw 2
Zad. 1
Narysować wykres wektorowy dla obwodu
Zad. 2
Obliczyć moce elementów w obwodzie i sporządzić bilans mocy.
Dane: , , , ,
Zad. 3
Obliczyć przebieg w stanie nieustalonym po przełączeniu w obwodzie
Dane: , , , , ,