PEE Moduł 7: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 463: | Linia 463: | ||
<math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | <math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | ||
|} | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd17.png]] | |||
|valign="top"|Z prawa komutacji dla kondensatora wynika, że <math>u_C(0^-)=u_C(0^+)</math> , stąd wobec <math>u_C(0^-)=0</math> otrzymuje się | |||
<math>0=E+A_1</math> | |||
oraz | |||
<math>A_1=-E</math> | |||
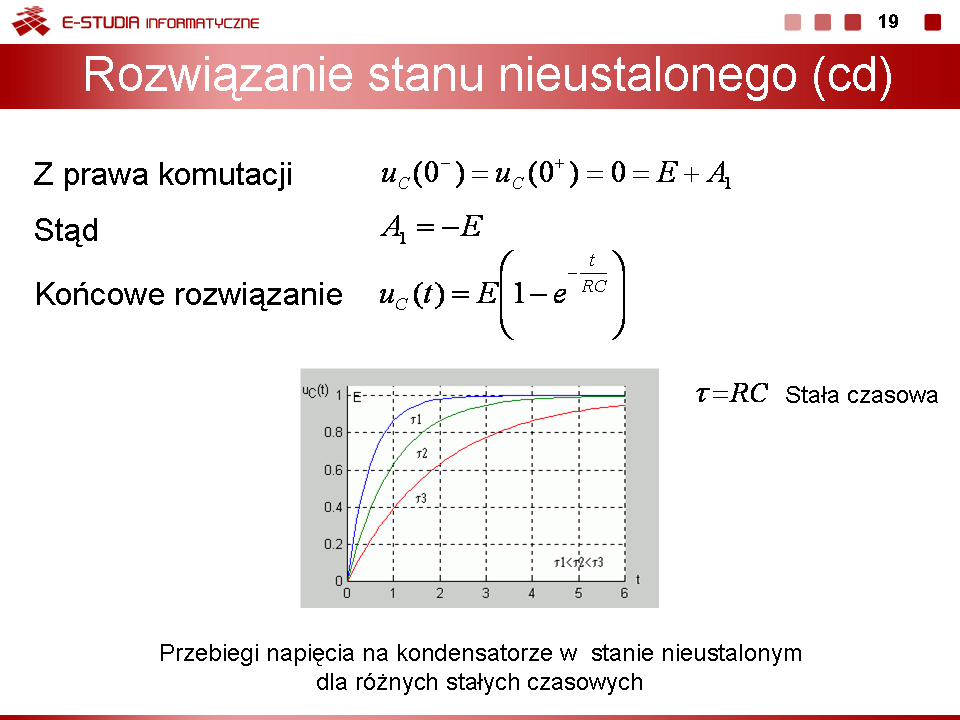
Rozwiązanie czasowe określające przebieg napięcia na kondensatorze przyjmuje więc postać | |||
<math>u_C(t)=E(1-e6{-\frac{t}{RC}})</math> | |||
| Linia 480: | Linia 504: | ||
Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera). | Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera). | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. | |||
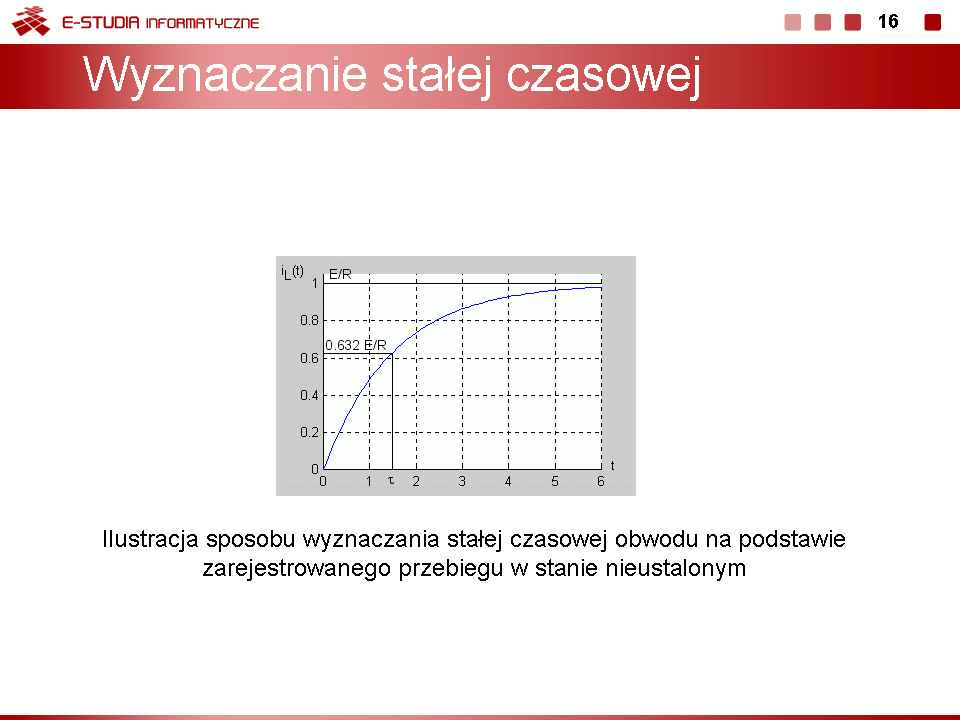
Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd18.png]] | ||
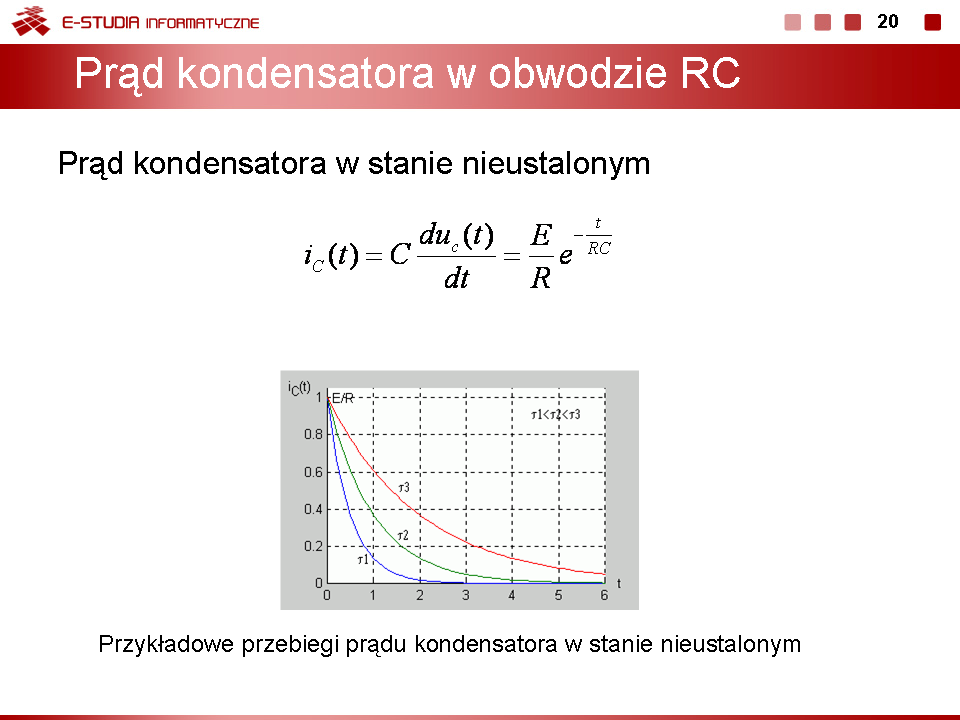
|valign="top"|Po określeniu funkcji opisującej przebieg napięcia na kondensatorze można określić przebieg czasowy prądu w obwodzie. Korzysta się przy tym z zależności definicyjnej kondensatora <math>i_C=C\frac{du_C}{dt}</math>, zgodnie z którą | |||
<math> | <math>i_C(t)=C\frac{du_c(t)}{dt}=\frac{E}{R}e^{-\frac{t}{RC}}</math> | ||
Przebieg prądu ładowania kondensatora w stanie nieustalonym w obwodzie RC dla różnych stałych czasowych przedstawia rysunek | |||
[[Grafika:PEE_M7_Slajd18.png]] | |||
|} | |} | ||
<hr width="100%"> | |||
Wersja z 09:49, 2 sie 2006

|
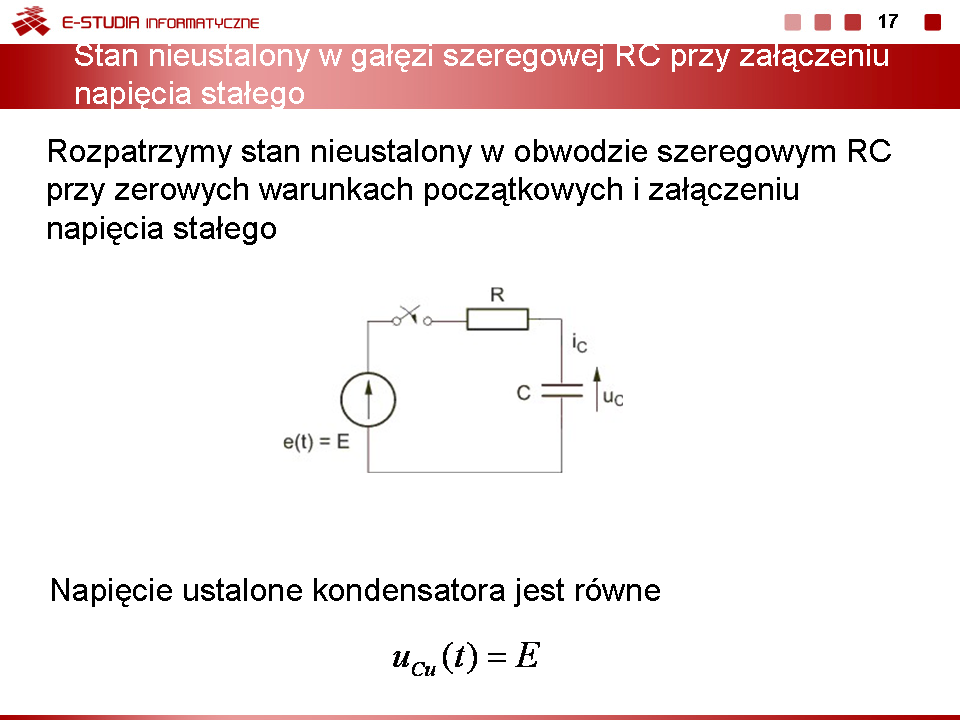
Metoda równań różniczkowych w rozwiązaniu stanu nieustalonego w obwodach elektrycznych |

|
Przykład
Napisać układ równań stanu dla obwodu elektrycznego przedstawionego na rysunku |
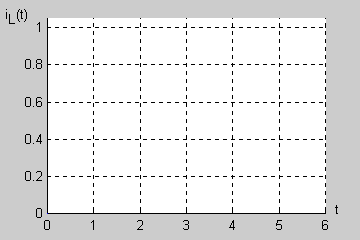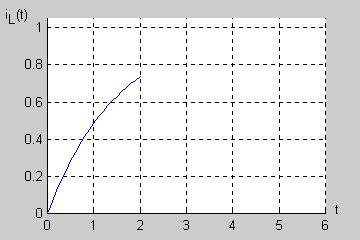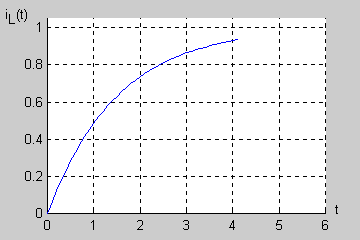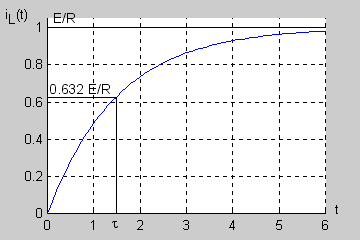
| Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość
|
| Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony.
Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL. |