PEE Moduł 10: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 476: | Linia 476: | ||
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów ([[PEE_Moduł_10#wzor_10_1|wzór]]). | Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów ([[PEE_Moduł_10#wzor_10_1|wzór]]). | ||
Na rysunku obok (slajd 12) przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki. | Na rysunku obok (slajd 12) przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki. | ||
| Linia 494: | Linia 495: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M10_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd13.png]] | ||
|valign="top"| | |valign="top"|'''Wybrane zastosowania czwórników''' | ||
'''Żyrator''' | |||
Żyrator jest czwórnikiem opisanym następującą macierzą łańcuchową | |||
: <math> | |||
\begin{bmatrix} | |||
U_1 \\ | |||
I_1 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
0 & R_z \\ | |||
G_z & 0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
U_2 \\ | |||
-I_2 | |||
\end{bmatrix} | |||
</math> | |||
Parametr <math>G_z</math> jest nazywany konduktancją żyracji a <math>R_z=1/G_z</math> rezystancją. Oznaczenia graficzne żyratora przedstawione są na rysunku obok (slajd 13). | |||
Znak minus występujący przy prądzie wyjściowym wynika z przyjętego zwrotu prądu wyjściowego (do pudełka). Równaniu łańcuchowemu żyratora odpowiada opis admitancyjny o postaci | |||
: <math> | |||
\begin{bmatrix} | |||
I_1 \\ | |||
I_2 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
0 & G_z \\ | |||
-G_z & 0 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
U_1 \\ | |||
U_2 | |||
\end{bmatrix} | |||
</math> | |||
Najważniejszą własnością żyratora jest przetwarzanie impedancji obciążenia w impedancję odwrotnie proporcjonalną do niej. Rozważmy układ żyratora obciążonego impedancją <math>Z_0</math> (rysunek na slajdzie 14). | |||
Impedancja wejściowa takiego układu zdefiniowana w postaci | |||
: <math>Z_{we}={U_1 \over I_1}</math> | |||
<math>A_{11}=0</math>, <math>A_{12}=R_z</math>, <math>A_{21}=G_z</math>, <math>A_{22}=0</math>, więc | |||
: <math>Z_{we}={A_{11}+A_{12}Y_0 \over A_{21}+A_{22}Y_0}={R_z^2 \over Z_0}</math> | |||
|} | |} | ||
| Linia 501: | Linia 553: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M10_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd14.png]] | ||
|valign="top"| | |valign="top"|Impedancja układu żyratora obciążonego impedancją <math>Z_0</math> jest odwrotnie proporcjonalna do impedancji obciążenia ze współczynnikiem proporcjonalności równym <math>R_z^2</math>. Jeśli żyrator zostanie obciążony kondensatorem o impedancji operatorowej równej <math>Z_0 = 1/sC</math> to impedancja wejściowa układu jest równa | ||
: <math>Z_{we}=sR_z^2C</math> | |||
Jest to postać odpowiadająca ogólnemu opisowi impedancji operatorowej cewki <math>Z_L=sL</math>. Zatem układ żyratora obciążonego pojemnością <math>C\,</math> przedstawia sobą cewkę o indukcyjności <math>L\,</math> | |||
: <math>L=R_z^2C</math> | |||
Powyższej zależności matematycznej można przyporządkować transformację układową zilustrowaną na rysunku obok (slajd 14). | |||
Żyrator jako czwórnik jest bardzo łatwo realizowalny w praktyce przy wykorzystaniu układów tranzystorowych lub wzmacniaczy operacyjnych. Z tego względu układy wykorzystujące żyratory są powszechnie stosowane w układach elektronicznych (np. filtrach) eliminując z nich cewki, trudno realizowalne w technologii scalonej. | |||
|} | |} | ||
| Linia 508: | Linia 570: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M10_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd15.png]] | ||
|valign="top"| | |valign="top"|'''Konwerter ujemno-impedancyjny (NIC)''' | ||
Konwerter ujemno-impedancyjny (NIC) jest czwórnikiem aktywnym (wytwarzającym energię) posiadającym własność przetwarzania prądu bądź napięcia z ujemnym znakiem. Wyróżnia się dwa rodzaje konwerterów ujemno-impedancyjnych | |||
*NIC z inwersją prądu (INIC) | |||
*: <math>\begin{bmatrix} | |||
U_1 \\ | |||
I_1 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & -K_i | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
U_2 \\ | |||
-I_2 | |||
\end{bmatrix} | |||
</math> | |||
*NIC z inwersją napięcia (VNIC) | |||
*: <math>\begin{bmatrix} | |||
U_1 \\ | |||
I_1 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
-K_u & 0 \\ | |||
0 & 1 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
U_2 \\ | |||
-I_2 | |||
\end{bmatrix} | |||
</math> | |||
Parametr <math>K\,</math> (<math>K_i</math> dla konwertera ujemno-impedancyjnego prądu oraz <math>K_u</math> dla konwertera ujemno-impedancyjnego napięcia) jest współczynnikiem przetwarzania bądź prądu bądź napięcia. W konwerterze INIC prąd wejściowy jest proporcjonalny do prądu wyjściowego z ujemnym współczynnikiem proporcjonalności <math>–K_i</math> przy niezmienionej wartości napięcia wejściowego. W konwerterze VNIC napięcie wejściowe jest proporcjonalne do napięcia wyjściowego z ujemnym współczynnikiem proporcjonalności <math>–K_u</math> przy niezmienionym prądzie wejściowym. | |||
|} | |} | ||
Wersja z 09:07, 2 sie 2006

|
Wykład10. Czwórniki |

|
Przykład
Wyznaczyć wyrażenie na transmitancję napięciową i impedancję wejściową czwórnika z poprzedniego przykładu. Rozwiązanie Macierz łańcuchowa czwórnika ma postać Transmitancja napięciowa w stanie jałowym na wyjściu jest więc równa Wobec braku obciążenia czwórnika przez impedancję nie przepływa prąd, stąd całe napięcie wyjściowe pochodzi z impedancji poprzecznej (dzielnik impedancyjny). Impedancja wejściowa czwórnika przy obciążeniu bramy wyjściowej impedancją na podstawie wzoru jest równa Jest ona funkcją wszystkich parametrów układu oraz impedancji obciążenia. |

|
Połączenie równoległe czwórników
Dwa czwórniki są połączone równolegle, jeśli spełnione są warunki:
Ponadto w tym przypadku należy zapewnić spełnienie warunków regularności połączenia zdefiniowanych odpowiednią równością prądów (wzory). Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że Przy większej liczbie czwórników połączonych równolegle macierz admitancyjna wypadkowa jest równa sumie macierzy admitancyjnych wszystkich czwórników występujących w połączeniu. Kolejność sumowania macierzy admitancyjnych nie odgrywa żadnej roli.
Dwa czwórniki są połączone szeregowo-równolegle, jeśli spełnione są warunki:
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów (wzór). Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa połączenia jest równa sumie macierzy hybrydowych każdego czwórnika. Oznacza to, że Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa , wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych wszystkich czwórników występujących w połączeniu. Kolejność sumowania macierzy hybrydowych nie odgrywa żadnej roli. |
|
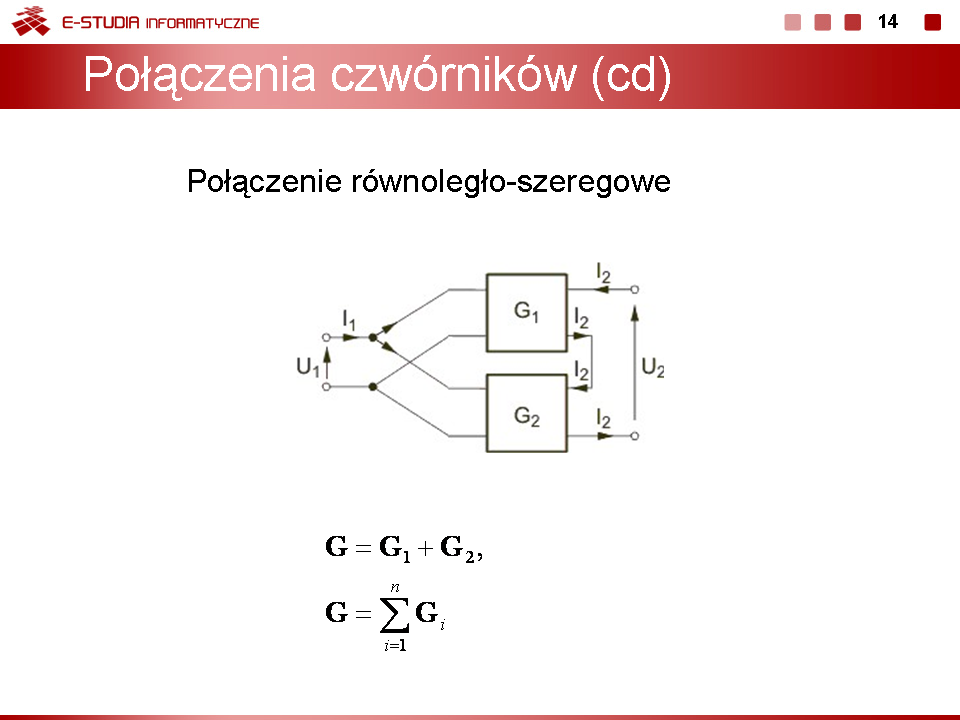
Połączenie równoległo-szeregowe czwórników
Dwa czwórniki są połączone równolegle-szeregowo, jeśli spełnione są warunki:
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów (wzór). Na rysunku obok (slajd 12) przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu równolegle-szeregowym czwórników macierz hybrydowa odwrotna połączenia jest równa sumie macierzy hybrydowych każdego czwórnika. Oznacza to, że Przy większej liczbie czwórników połączonych równolegle-szeregowo macierz hybrydowa odwrotna , wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych wszystkich czwórników występujących w połączeniu. Kolejność sumowania macierzy nie odgrywa żadnej roli. |

|










