PEE Moduł 10: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 15: | Linia 15: | ||
: <math>I_1=I_1^'</math><span id="wzor_10_1"></span> | : <math>I_1=I_1^'</math><span id="wzor_10_1"></span> | ||
: <math>I_2=I_2^'</math> | : <math>I_2=I_2^'</math><span id="wzor_10_2"></span> | ||
jak to zaznaczono na rysunku. Sygnały prądu i napięcia po stronie wejściowej oznaczać będziemy ze wskaźnikiem 1, a po stronie wyjściowej – ze wskaźnikiem 2. Przyjmiemy umownie, że oba prądy: na wejściu i wyjściu są zwrócone do prostokąta oznaczającego czwórnik. | jak to zaznaczono na rysunku. Sygnały prądu i napięcia po stronie wejściowej oznaczać będziemy ze wskaźnikiem 1, a po stronie wyjściowej – ze wskaźnikiem 2. Przyjmiemy umownie, że oba prądy: na wejściu i wyjściu są zwrócone do prostokąta oznaczającego czwórnik. | ||
| Linia 429: | Linia 429: | ||
Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. | Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. | ||
Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna <math>Y\,</math> połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że | |||
: <math>Y=Y_1+Y_2</math> | |||
Przy większej liczbie czwórników połączonych równolegle macierz admitancyjna wypadkowa jest równa sumie macierzy admitancyjnych wszystkich czwórników występujących w połączeniu. | |||
: <math>Y=\sum_{i=1}^n Y_i</math> | |||
Kolejność sumowania macierzy admitancyjnych nie odgrywa żadnej roli. | |||
'''Połączenie szeregowe-równoległe czwórników''' | |||
Dwa czwórniki są połączone szeregowo-równolegle, jeśli spełnione są warunki: | |||
*prąd wejściowy każdego czwórnika jest taki sam a napięcie wejściowe połączenia jest równe sumie napięć wejściowych każdego czwórnika | |||
*prąd wyjściowy połączenia jest równy sumie prądów wyjściowych każdego czwórnika a napięcie wyjściowe obu czwórników jest takie samo. | |||
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów ([[PEE_Moduł_10#wzor_10_2|wzór]]). | |||
Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki. | |||
Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa <math>H\,</math> połączenia jest równa sumie macierzy hybrydowych <math>H\,</math> każdego czwórnika. Oznacza to, że | |||
: <math>H=H_1+H_2</math> | |||
Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa <math>H\,</math>, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych <math>H\,</math> wszystkich czwórników występujących w połączeniu. | |||
: <math>H=\sum_{i=1}^n H_i</math> | |||
Kolejność sumowania macierzy hybrydowych nie odgrywa żadnej roli. | |||
|} | |} | ||
Wersja z 08:44, 2 sie 2006

|
Wykład10. Czwórniki |

|
Przykład
Wyznaczyć wyrażenie na transmitancję napięciową i impedancję wejściową czwórnika z poprzedniego przykładu. Rozwiązanie Macierz łańcuchowa czwórnika ma postać Transmitancja napięciowa w stanie jałowym na wyjściu jest więc równa Wobec braku obciążenia czwórnika przez impedancję nie przepływa prąd, stąd całe napięcie wyjściowe pochodzi z impedancji poprzecznej (dzielnik impedancyjny). Impedancja wejściowa czwórnika przy obciążeniu bramy wyjściowej impedancją na podstawie wzoru jest równa Jest ona funkcją wszystkich parametrów układu oraz impedancji obciążenia. |

|
Połączenie równoległe czwórników
Dwa czwórniki są połączone równolegle, jeśli spełnione są warunki:
Ponadto w tym przypadku należy zapewnić spełnienie warunków regularności połączenia zdefiniowanych odpowiednią równością prądów (wzory). Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że Przy większej liczbie czwórników połączonych równolegle macierz admitancyjna wypadkowa jest równa sumie macierzy admitancyjnych wszystkich czwórników występujących w połączeniu. Kolejność sumowania macierzy admitancyjnych nie odgrywa żadnej roli.
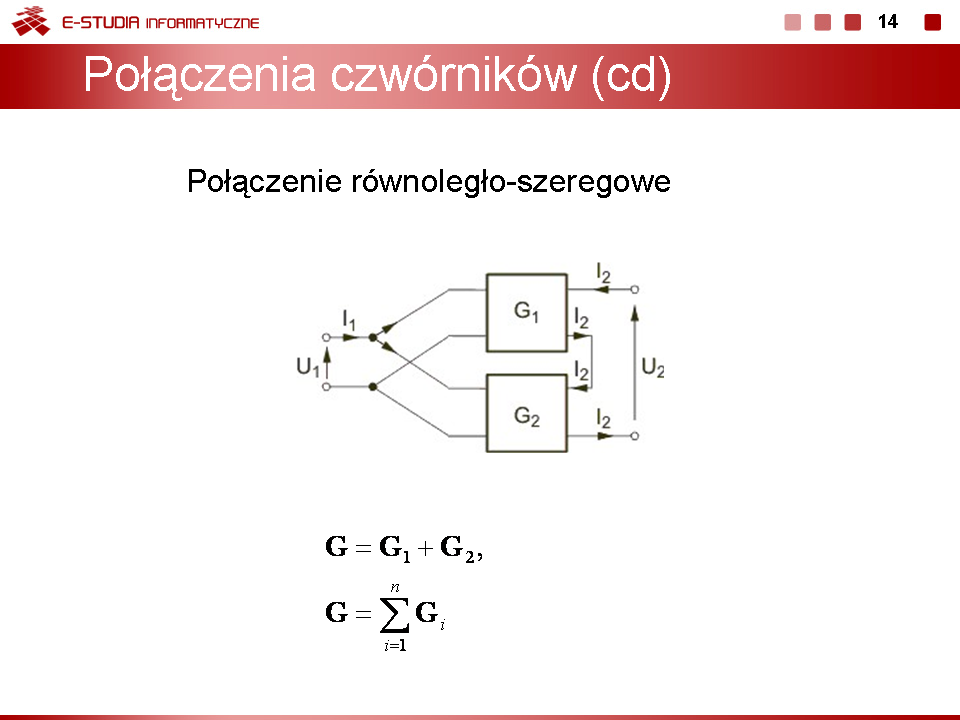
Dwa czwórniki są połączone szeregowo-równolegle, jeśli spełnione są warunki:
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów (wzór). Na rysunku obok (slajd 11) przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa połączenia jest równa sumie macierzy hybrydowych każdego czwórnika. Oznacza to, że Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa , wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych wszystkich czwórników występujących w połączeniu. Kolejność sumowania macierzy hybrydowych nie odgrywa żadnej roli. |
|

|

|

|

|







