Matematyka dyskretna 1/Wykład 3: Zliczanie zbiorów i funkcji: Różnice pomiędzy wersjami
Nie podano opisu zmian |
|||
| Linia 45: | Linia 45: | ||
** jest zwartym zapisem, że <math>f</math> jest funkcją postaci <math>f : \mathbb{N} \longrightarrow \mathbb{N}</math> <br> daną przepisem <math>f(n) = 2n</math> | ** jest zwartym zapisem, że <math>f</math> jest funkcją postaci <math>f : \mathbb{N} \longrightarrow \mathbb{N}</math> <br> daną przepisem <math>f(n) = 2n</math> | ||
** jako przeciwdziedzinę określiliśmy zbiór liczb naturalnych, <br> ale w istocie wartościami tej funkcji są tylko liczby parzyste | ** jako przeciwdziedzinę określiliśmy zbiór liczb naturalnych, <br> ale w istocie wartościami tej funkcji są tylko liczby parzyste | ||
* <math>g : \mathbb{N} \longrightarrow \mathbb{R}, \ | * <math>g : \mathbb{N} \longrightarrow \mathbb{R}, \ g(n) = n/2</math>, | ||
** określenie <math>g : \mathbb{N} \longrightarrow \mathbb{N}</math> nie byłoby tu prawidłowe, gdyż wartość <math>n/2</math> nie zawsze jest liczbą naturalną | ** określenie <math>g : \mathbb{N} \longrightarrow \mathbb{N}</math> nie byłoby tu prawidłowe, gdyż wartość <math>n/2</math> nie zawsze jest liczbą naturalną | ||
* <math>h : \mathbb{N} \longrightarrow {\left\{ {13} \right\}\ }, \ h(n) = 13</math>, | * <math>h : \mathbb{N} \longrightarrow {\left\{ {13} \right\}\ }, \ h(n) = 13</math>, | ||
** to też jest poprawnie określona funkcja, mimo że niezbyt frapująca (tzw. funkcja stała) | ** to też jest poprawnie określona funkcja, mimo że niezbyt frapująca (tzw. funkcja stała) | ||
* <math>f : \mathbb{N} \longrightarrow \mathbb{N}, \ | * <math>f : \mathbb{N} \longrightarrow \mathbb{N}, \ f(n) = (1 + 3 + 5 + \ldots + (2n+1))^n</math>. | ||
** takie określenie też jest poprawne, choć nie od razu widać, ile to jest | ** takie określenie też jest poprawne, choć nie od razu widać, ile to jest | ||
* <math>g : \mathbb{R} \ni x \mapsto \sin\frac{x}{\pi}\in \mathbb{R}</math> jest całkiem poprawną funkcją. | * <math>g : \mathbb{R} \ni x \mapsto \sin\frac{x}{\pi}\in \mathbb{R}</math> jest całkiem poprawną funkcją. | ||
| Linia 62: | Linia 62: | ||
<center><math>x \mapsto a_nx^n + a_{n-1}x^{n-1} + \ldots + a_2x^2 + a_1 x + a_0 | <center><math>x \mapsto a_nx^n + a_{n-1}x^{n-1} + \ldots + a_2x^2 + a_1 x + a_0</math></center> | ||
</math></center> | |||
Aktualna wersja na dzień 22:22, 15 wrz 2023
Funkcje
Ten fragment wykładu przypomina poznany już wcześniej materiał. Służy jedynie ustaleniu terminologii i notacji.
Funkcja o dziedzinie i przeciwdziedzinie to dowolna relacja taka, że:
Pierwszy warunek mówi, że każdy element dziedziny ma jakąś wartość przypisaną funkcją . Drugi, że taka wartość jest co najwyżej jedna (dowolne dwie są bowiem równe). W skrócie oba warunki możemy zapisać łącznie jako
gdzie kwantyfikator oznacza istnieje dokładnie jeden.
- Ważne jest
- wykorzystanie wszystkich elementów dziedziny: każdemu elementowi dziedziny ...
- i jednoznaczność: jest przyporządkowany dokładnie jeden element przeciwdziedziny,
- nie wyklucza to sytuacji, gdy np. dwóm elementom dziedziny przyporządkowany jest ten sam element przeciwdziedziny,
- nie każdy element przeciwdziedziny musi być wykorzystany, tzn. mogą istnieć takie elementy przeciwdziedziny, które nie są przyporządkowane żadnemu elementowi dziedziny,
- dziedzina i przeciwdziedzina mogą być tym samym zbiorem.
Notacja:
- Piszemy lub na oznaczenie funkcji o nazwie , której dziedziną jest zbiór , a przeciwdziedziną zbiór .
- elementy dziedziny nazywamy argumentami funkcji
- elementy przeciwdziedziny im przyporządkowane nazywamy wartościami funkcji.
- Piszemy lub na oznaczenie tego, że funkcja elementowi przyporządkowuje element
- mówimy wtedy, że jest wartością funkcji na argumencie .
- Często podaje się przepis na funkcję, wykorzystując
- operacje arytmetyczne:
- lub inne powszechnie znane funkcje .
- W powyższych przykładach dziedziny i przeciwdziedziny można się domyślić (zapewne liczby rzeczywiste), ale dla ścisłości powinno się je podać, np. .
Przykłady funkcji
Najczęściej będziemy się zajmowali funkcjami, które działają na liczbach (dziedziną i przeciwdziedziną będą zbiory liczbowe, np. ), ale można mówić o funkcjach na różnych zbiorach.
- ,
- jest zwartym zapisem, że jest funkcją postaci
daną przepisem - jako przeciwdziedzinę określiliśmy zbiór liczb naturalnych,
ale w istocie wartościami tej funkcji są tylko liczby parzyste
- jest zwartym zapisem, że jest funkcją postaci
- ,
- określenie nie byłoby tu prawidłowe, gdyż wartość nie zawsze jest liczbą naturalną
- ,
- to też jest poprawnie określona funkcja, mimo że niezbyt frapująca (tzw. funkcja stała)
- .
- takie określenie też jest poprawne, choć nie od razu widać, ile to jest
- jest całkiem poprawną funkcją.
- ,
- to określenie (mimo, że podobne do poprzedniego) jest błędne:
nie da się policzyć wartości ;
należałoby więc napisać np.
- to określenie (mimo, że podobne do poprzedniego) jest błędne:
- ,
- to funkcja określona na słowach nad alfabetem dwuelementowym
- każdemu słowu przypisuje to słowo rozszerzone na końcu o symbol
- długość słowa
Wielomian to funkcja:
gdzie
- liczby zwane są współczynnikami wielomianu
- mówimy więc o wielomianach o współczynnikach
- naturalnych - jeśli
- całkowitych - jeśli
- wymiernych - jeśli
- rzeczywistych - jeśli
- liczba zwana jest stopniem wielomianu, ale tylko o ile .
- mówimy więc o wielomianach o współczynnikach
Surjekcje, injekcje i bijekcje
Surjekcja to funkcja spełniająca warunek
- Intuicyjnie, funkcja jest surjekcją, jeśli jej cała przeciwdziedzina jest wykorzystana, tzn. każdy jej element jest wartością funkcji dla jakiegoś elementu dziedziny,
- surjekcje często są nazywane funkcjami "na",
- piszemy też wtedy .
Przykład
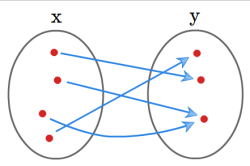
Funkcja jest surjekcją.
Funkcja nie jest surjekcją.
Funkcja nie jest surjekcją.
Funkcja jest surjekcją.
Funkcja jest surjekcją.
Funkcja jest surjekcją.
Funkcja nie jest suriekcją.
Funkcja nie jest surjekcją.
Funkcja nie jest suriekcją.
Funkcja jest suriekcją.
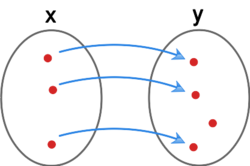
Injekcja to funkcja spełniająca warunek:
- Intuicyjnie, funkcja jest injekcją, jeśli różnym elementom dziedziny funkcja przyporządkowuje różne elementy przeciwdziedziny,
- injekcje często są nazywane funkcjami różnowartościowymi,
- piszemy też wtedy .
Przykład
Funkcja jest injekcją.
Funkcja nie jest injekcją.
Funkcja jest injekcją.
Funkcja nie jest injekcją.
Funkcja jest injekcją.
Funkcja jest injekcją.
Funkcja nie jest injekcją.
Funkcja jest injekcją.
Funkcja nie jest injekcją.
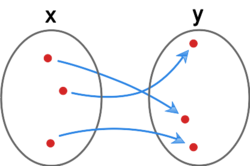
Bijekcja to funkcja, która jest jednocześnie surjekcją i injekcją.
Przykład
Funkcja jest bijekcją.
Funkcja nie jest bijekcją.
Funkcja nie jest bijekcją.
Funkcja jest bijekcją.
Funkcja jest bijekcją.
Funkcja nie jest bijekcją.
Funkcja nie jest bijekcją.
Funkcja nie jest bijekcją.
Funkcja nie jest bijekcją.
Funkcje odwrotne
Traktując funkcję jako relację (zbiór par), możemy rozważać relację odwrotną do .
Kiedy ta relacja jest funkcją?
- ponieważ ma spełniać warunek, że każdy element dziedziny (tzn. zbioru ) ma przypisaną jakąś wartość, oznacza to, że sama funkcja wyczerpuje wszystkie elementy przeciwdziedziny, a zatem, że jest surjekcją,
- nadto ma przypisywać dokładnie jeden taki element, czyli że każdy element z jest przypisany poprzez jednemu elementowi z , a zatem musi być injekcją.
A zatem: funkcja posiada funkcję odwrotną, wtedy i tylko wtedy, gdy jest bijekcją.
- Nieformalnie tworzenie funkcji odwrotnej polega na odwracaniu strzałek.
- Gdyby nie była surjekcją, to przy próbie odwrócenia strzałek niektóre elementy zbioru nie miałyby przyporządkowanego żadnego elementu z .
- Gdyby zaś nie była injekcją, to przy próbie odwrócenia strzałek niektóre strzałki byłyby "rozdwojone".
Przykład
- Funkcja jest bijekcją, a zatem posiada funkcję odwrotną. Tę funkcję odwrotną można wyliczyć: skoro , to . Zatem .
- Funkcja nie jest injekcją. Nie posiada więc funkcji odwrotnej.
- Funkcja nie jest surjekcją. Nie posiada więc funkcji odwrotnej. Ale rozważając tę funkcję z przeciwdziedziną będącą zbiorem liczb parzystych, tzn. staje się ona bijekcją i posiada funkcję odwrotną .
- Funkcja nie jest ani injekcją ani surjekcją. Nie posiada więc funkcji odwrotnej. Surjektywność można by "uratować", rozważając
Wciąż jednak brakowałoby injektywności. Ograniczając jednak, tę funkcję do liczb nieujemnych, tzn. traktując ją jako:
staje się już bijekcją, więc posiada funkcję odwrotną, którą jest
Składanie funkcji
Złożenie funkcji i funkcji to funkcja
określona dla wszystkich argumentów jako .
- Nieformalnie - najpierw obliczamy wartość funkcji dla elementu ,
a następnie obliczamy wartość funkcji dla wyniku tego obliczenia; czyli "idziemy dalej wzdłuż następnej strzałki"
- Piszemy (a nie ) na oznaczenie złożenia, w którym najpierw obliczana jest wartość funkcji , a potem funkcji .
- W praktyce, przy złożeniu , dziedzina funkcji nie musi być tym samym zbiorem, co przeciwdziedzina funkcji - wystarczy, by była większa.
Przykład
- Niech i . Wówczas dla mamy a dla mamy .
Morał: złożenia i to (na ogół) różne funkcje.
- Niech i . Wówczas złożenie dane jest wzorem
Morał: Nie zawsze da się łatwo wyliczyć przepis na funkcję złożoną.
- Gdy jest bijekcją, to istnieje funkcja odwrotna . Jeśli złożymy , to uzyskamy funkcję , która "nic nie robi":
Taka funkcja zwana jest identycznością na zbiorze i oznaczana . Podobnie - składając , otrzymamy identyczność na zbiorze .
Widzieliśmy, że nie zawsze .
Obserwacja 3.1
Dla funkcji zachodzi .
Obserwacja 3.2
Nadto dla mamy:
- Jeśli są surjekcjami, to jest surjekcją.
- Jeśli są injekcjami, to jest injekcją.
- Jeśli są bijekcjami, to jest bijekcją.
- Pierwsza i trzecia z powyższych własności nie zachodzą, jeśli dziedzina funkcji jest większa niż przeciwdziedzina funkcji .
Przykład
Zbadaj czy dla funkcji zachodzi:
- jeśli jest surjekcją, to jest surjekcją
- jeśli jest surjekcją, to jest surjekcją
- jeśli jest injekcją, to jest injekcją
- jeśli jest injekcją, to jest injekcją
Funkcje wielu zmiennych
- Funkcja dwóch zmiennych to funkcja, której dziedziną jest zbiór par (zamiast pojedynczych elementów).
- Piszemy np. .
- Zatem funkcja taka każdej parze przyporządkowuje dokładnie jeden element .
- Podobnie można zdefiniować funkcje trzech i więcej zmiennych.
Przykład
Przykładem funkcji dwóch zmiennych są działania arytmetyczne:
a także konkatenacja (sklejenie) słów
- , gdzie oznacza słowo (krotkę) powstałe z doklejenia słowa na końcu słowa .
Zliczanie zbiorów

Gdy chcemy policzyć liczbę samochodów na parkingu zazwyczaj wskazujemy na kolejne samochody odliczając: jeden, dwa, trzy, itd., aż do momentu gdy każdy samochód zostanie wskazany. Wtedy ostatnia liczba, którą wypowiedzieliśmy jest uważana za liczbę samochodów na parkingu.
Aby wprowadzić matematyczny model procedury zliczania definiujemy początkowe odcinki liczb naturalnych:
Załóżmy, że na parkingu stoi samochodów. Zliczając je wybieramy elementy (zazwyczaj kolejne liczby) i przypisujemy je do samochodów na parkingu. Uwaga: wybierając liczby z zaczynamy od i kończymy na (na ogół nie-informatycy zliczają od do ). Określamy zatem w trakcie tego zliczania bijekcję ,
gdzie jest zbiorem samochodów na parkingu. W istocie jest to bijekcja, bo dwa różne samochody mają różne numery (injektywność)
i każdy samochód jest policzony (surjektywność).
Obserwacja 3.3
Gdy , to nie istnieje injekcja z w .
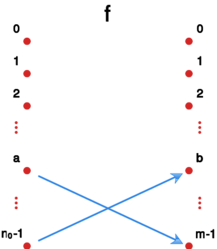
Dowód
Niech będzie zbiorem liczb naturalnych takich, że istnieje injekcja postaci , przy pewnym . Oczywiście , bo nie istnieje liczba naturalna taka, że . Także , bo nie istnieje funkcja z niepustego zbioru w pusty . Dla dowodu niewprost załóżmy, że jest niepusty. Wtedy, z Zasady Minimum, ma element najmniejszy, powiedzmy math>n_0>1</math>. Istnieje zatem i injekcja . Analogicznie jak wcześniej oraz , bo inaczej wszystkie elementy musiałyby mieć tę samą wartość, co stoi w sprzeczności z injektywnością . Zatem jest dodatnią liczbą naturalną.
Jeśli , to restrykcja jest injekcją z w , czyli co stoi w sprzeczności z minimalnością w .
Jeśli , to niech i będą takimi liczbami, że i .
Wtedy funkcja zadana przez
jest injekcją, bo dla zachodzi i dodatkowo . Zatem znów , co stoi w sprzeczności z minimalnością w .
Wniosek 3.4
Jeśli istnieje bijekcja ze zbioru na , to .
Zbiór skończony to zbiór bijektywny z pewnym zbiorem postaci .
Zbiór nieskończony to zbiór, który nie jest skończony.
Jeśli jest zbiorem skończonym, to Wniosek 3.4 gwarantuje nam, że jest bijektywny z dokładnie jednym zbiorem postaci . Rozważając skończony zbiór -elementowy , często używamy notacji ukrywającej w sobie bijekcję postaci .
Liczba elementów skończonego zbioru , to
jedyna liczba naturalna taka, że istnieje bijekcja z w . Liczbę te oznaczamy
przez .
Przykład
Oczywiście . W szczególności zbiór pusty ma, zgodnie z intuicją, liczbę elementów równą .
Przykład
Zbiór liczb parzystych jest nieskończony.
Dla dowodu niewprost załóżmy, że , tzn. . Oczywiście , bo . Nadto suma wszystkich jest ograniczeniem zbioru , a więc, z Zasady Maksimum, posiada element największy, powiedzmy . Ponieważ jest największą liczbą parzystą, , co oczywiście daje sprzeczność.
Obserwacja 3.5
Zbiór jest nieskończony wtedy i tylko wtedy, gdy istnieje injekcja z w .
Dowód
Załóżmy, że jest nieskończony i zdefiniujmy indukcyjnie funkcję , kładąc:
- niech będzie dowolnym, wybranym elementem ,
- gdy są już określone, wtedy niech będzie dowolnie wybranym elementem z .
To, że wyboru opisanego w punkcie drugim możemy zawsze dokonać, wynika wprost z nieskończoności zbioru . Istotnie, gdyby zbiór był pusty, to byłoby bijekcją świadczącą o tym, że jest skończony. Oczywiście, tak zdefiniowana funkcja jest injekcją.
Dla dowodu implikacji odwrotnej załóżmy, że istnieje injekcja oraz że jest skończony tzn. że istnieje bijekcja dla pewnego . Zauważmy, że restrykcja jest również injekcją. A zatem złożenie jest injekcją z w , co stoi w sprzeczności z Obserwacją 3.3.
Zbiór przeliczalny to zbiór skończony lub bijektywny z .
Przykład
- zbiór pusty jest przeliczalny, bo jest skończony,
- zbiór liczb parzystych jest przeliczalny, bo jest bijekcją
- zbiór liczb całkowitych jest przeliczalny, bo
jest bijekcją z w .
Zasada Szufladkowa
Wróćmy jeszcze do Obserwacji 3.3 - formalnej podstawy zliczania skończonych zbiorów. Ma ona także bardziej praktyczną interpretację. Jest to formalne ujęcie faktu powszechnie znanego jako Zasada Szufladkowa Dirichleta (wierzy się, że jako pierwszy opisał ja Dirichlet w 1834).
Wniosek 3.6 [Zasada Szufladkowa Dirichleta]
Jeśli obiektów jest rozmieszczonych w szufladach i , to istnieje szuflada z przynajmniej dwoma obiektami.
Dowód
Zbiór obiektów jest bijektywny ze zbiorem , zaś zbiór szuflad z . Rozmieszczenie obiektów w szufladach to określenie funkcji z w . Ponieważ to Obserwacja 3.3 mówi nam, ze funkcja ta nie jest injekcją, a zatem lokuje co najmniej dwa obiekty w tej samej szufladzie.
Przykład
Proste przykłady:
- Wśród mieszkańców Krakowa co najmniej dwie osoby mają tę samą liczbę włosów na głowie.
Dowód
Rzeczywiście, liczba włosów na głowie człowieka nie przekracza , natomiast liczba mieszkańców Krakowa przekracza . Weźmy szufladek ponumerowanych kolejnymi liczbami naturalnymi od do i wkładajmy do szufladki o danym numerze osoby, które mają taką liczbę włosów na głowie, jak numer szufladki. Ponieważ osób jest , a szufladek , z Zasady Szufladkowej wynika, że w jednej szufladce muszą znaleźć się co najmniej dwie osoby.
- W grupie osób muszą być co najmniej dwie, które urodziły się w tym samym miesiącu.
Dowód
Weźmy szufladek z nazwami miesięcy i wkładajmy do nich osoby, które urodziły się w danym miesiącu. Ponieważ osób jest , a szufladek , w jednej z nich muszą być co najmniej dwie osoby.
Czasem, umiejętnie dobierając "pudełka" można pokazać bardziej zaskakujące fakty...
Przykład
Pewna grupa osób wita się podając sobie ręce. Nikt nie wita się z samym sobą i żadna para osób nie wita się podwójnie. Czy muszą być dwie osoby, które witały taką samą liczbę osób?
- Gdy jest osób, to każda z nich przywita lub lub lub ... osób.
- Utwórzmy więc szuflad z etykietami i umieśćmy osobę w szufladzie o etykiecie , jeśli witała się z dokładnie osobami.
- Skoro jest osób i szuflad, to ...
niewiele z tego wynika :-( - Ale... niewiele wynika tylko jeśli wszystkie szuflady będą zajęte, a tak jest w przypadku, gdy również dwa konkretne pudełka o etykietach i są zajęte. Tyle, że nie jest to możliwe - nie może być osoby, która przywitała wszystkie pozostałe i równocześnie takiej, która nie przywitała nikogo.
- A zatem osób zajęło co najwyżej szuflad, więc w jednej z nich są co najmniej dwie osoby - takie, które przywitały tę samą liczbę osób.
Przykład
Wybierając liczb spośród , wśród wybranych liczb zawsze znajdziemy dwie, z których jedna dzieli drugą.
Istotnie:
- Określmy relacje na liczbach naturalnych, tak by:
Oznacza to, że jeśli liczby mają ten sam największy czynnik nieparzysty.
- Szufladami niech będą klasy równoważności relacji .
- Ile jest klas-szuflad dla liczb ze zbioru ? Co najwyżej , gdyż tyle może być liczb nieparzystych w zbiorze .
- Skoro wybrano , to rozkładając je do naszych szuflad jakieś dwie, powiedzmy muszą trafić do wspólnej szuflady.
Oznacza to, że któryś z ilorazów jest dodatnią potęgą dwójki, a zatem dzieli lub dzieli .
Przykład
Wybierzmy dowolnie różnych liczb naturalnych spośród . Pokażemy, że w zbiorze można wybrać dwa rozłączne podzbiory, dające tę samą sumę.
Istotnie:
- Szuflady poetykietujmy liczbami reprezentującymi możliwe sumy liczb w co najwyżej 10-cio elementowych podzbiorach zbioru . Ponieważ największa możliwa taka suma to , to mamy szuflad z etykietami:
- z drugiej strony -cio elementowy zbiór ma podzbiory, więc muszą być dwa podzbiory zbioru o tej samej sumie.
- Te dwa podzbiory nie muszą być rozłączne. Ale jeśli z obu z nich usuniemy wspólne liczby, to pozostałe dalej będą dawać takie same sumy, a powstałe zbiory będą już rozłączne.
Zasady zliczania
Bardzo często w tym kursie będziemy stać przed problemem zliczenia pewnego skończonego zbioru obiektów. Skrajnie niewygodne i nieefektywne byłoby, gdybyśmy za każdym razem konstruowali bijekcję z w nasz zbiór dla pewnego naturalnego . Na szczęście istnieje wiele reguł pozwalających szybciej zliczać obiekty kombinatoryczne. Poniżej przedstawiamy te podstawowe. Pierwsza z nich jest bardzo prosta i w sposób intuicyjny stosowana od początków cywilizacji.
Zasada dodawania
Dla skończonych i rozłącznych zbiorów i mamy:
Dowód
Niech liczności zbiorów , będą poświadczone bijekcjami i . Wtedy funkcja zadana przez:
jest bijekcją. Istotnie, skoro zbiory i są rozłączne, to dla dowolnych , zachodzi . Ponadto restrykcje do zbiorów zbiorów i są injekcjami. A zatem jest injekcją.
Dla dowodu surjektywności weźmy dowolny element . Załóżmy, że (w drugim przypadku dowód przebiega analogicznie). Wtedy z surjektywności wiemy, że istnieje takie, że . Ale . Zatem jest surjekcją.
Łatwy dowód indukcyjny pozwala uogólnić zasadę dodawania na dowolnie wiele skończonych zbiorów.
Wniosek 3.7
Dla zbiorów skończonych i parami rozłącznych:
Więcej pracy wymaga analiza sytuacji, gdy zbiory nie są rozłączne.
Zasada włączania i wyłączania
Dla zbiorów skończonych zachodzi
W szczególności, ,
o ile tylko są skończone.
Dowód
Zaczniemy od dowodu drugiego zdania. Ponieważ trzy zbiory i są parami rozłączne i sumują się do , na mocy Wniosku 3.7 mamy:
skąd
skąd już natychmiast dostajemy:
(1)
W sytuacji dowolnie wielu zbiorów użyjemy rozumowania indukcyjnego. Oczywiście twierdzenie jest prawdziwe.
Załóżmy, że . Na mocy równości (1) otrzymujemy:
Wykorzystując założenie indukcyjne dla wartości zachodzi
Rodzina wszystkich podzbiorów zbioru liczb można podzielić na dwie rozłączne rodziny:
- pierwsza składa się z tych , które nie zawierają , czyli
- druga jest rodziną tych , które zawierają , czyli .
W rezultacie otrzymujemy, że
co kończy dowód.
Wniosek 3.7 pozwala uogólnić Zasadę Szufladkową. Załóżmy, że pewna ilość obiektów jest rozmieszczona w szufladach. Niech będzie zbiorem obiektów w -tej szufladce. Ponieważ zbiory obiektów w różnych szufladach są rozłączne, to ilość obiektów we wszystkich szufladach wynosi . Zatem jeśli każda szufladka ma co najwyżej obiektów, to w sumie jest co najwyżej obiektów.
Uogólniona Zasada Szufladkowa
Jeśli obiektów rozmieszczonych jest w szufladach i , dla pewnego naturalnego , to istnieje szufladka z co najmniej obiektami.
Przypomnijmy, że iloczyn kartezjański (produkt) zbiorów i to zbiór
Zasada Mnożenia
Dla skończonych zbiorów :
Dowód
Najpierw pokażemy, że . W tym celu pokażemy, że funkcja
jest bijekcją.
Dla dowodu injektywności załóżmy, że , czyli . Bez straty ogólności możemy założyć, że , wtedy . Lewa strona równości jest wielokrotnością , zaś prawa leży w zbiorze , gdyż . Ponieważ jest jedyną wielokrotnością liczby w tym zbiorze, to i , co dowodzi injektywności .
Dla dowodu surjektywności rozważmy . Niech będzie największą liczbą taką, że . Wtedy zatem istnieje takie, że , co było do udowodnienia.
Załóżmy teraz, że i . Wtedy, z poczynionej wyżej obserwacji, dowód Zasady Mnożenia jest natychmiastowy, gdyż
Przykład
Rozważ turniej rycerski między bractwem czerwonych a bractwem niebieskich. Bractwo czerwonych ma rycerzy, bractwo niebieskich . Ile różnych indywidualnych pojedynków może być stoczonych, jeśli rycerze z tego samego bractwa nigdy ze sobą nie walczą?
- Niech i będą zbiorami rycerzy, odpowiednio z bractwa czerwonych i z bractwa niebieskich,
- każdy pojedynek może być interpretowany jako uporządkowana para , gdzie , . Zatem liczba pojedynków to liczność zbioru .
- .
Zliczanie podzbiorów
Zbiór potegowy, lub inaczej zbiór podzbiorów, zbioru oznaczamy przez .
Przykład
- i
- i
Przykład
Ile podzbiorów ma skończony zbiór -elementowy? Łatwo jest odpowiedzieć na to pytanie dla małych liczb . Np. zbiór ma następujące cztery podzbiory:
a zbiór trzyelementowy ma osiem podzbiorów:
Spróbujmy odpowiedzieć na to pytanie w ogólnej sytuacji i w sposób rekurencyjny.
i można wysunąć hipotezę, że w ogólności . Ale jak ją uzasadnić?
Załóżmy, że znamy liczbę i chcemy policzyć . Niech więc zbiór ma elementów, czyli po usunięciu ze zbioru elementu dostajemy -elementowy zbiór . Podobnie jak w dowodzie Zasady Włączania-Wyłączania, podzbiory zbioru można podzielić na dwa typy:
- albo mają w sobie element ,
- albo go nie mają.
W drugim przypadku są to podzbiory zbioru . Jest więc ich dokładnie .
Każdy zaś podzbiór pierwszego typu, czyli takie, że jest jednoznacznie wyznaczony przez swoje pozostałe elementy, tzn. elementy różne od . A zatem każdy taki zbiór , że , jest postaci dla pewnego . A zatem podzbiorów zbioru , w których jest element jest też tyle ile podzbiorów zbioru , tzn. .
Łącznie więc zbiór ma podzbiorów, czyli Teraz już bez trudu stwierdzamy, że to wraz z warunkiem jest spełnione przez
co można łatwo uzasadnić przez indukcję.
Obserwacja 3.8
Dla dowolnego, skończonego zbioru
Zliczanie funkcji
Zbiór funkcji postaci oznaczamy przez .
Obserwacja 3.9
Dla skończonych zbiorów mamy:
Dowód
Niech oraz . Każda funkcja to krotka wartości dla kolejnych :
A więc zbiór funkcji z w jest równoliczny z . Z Zasady Mnożenia otrzymujemy więc:
Przykład
Trzech kolegów: Bartek, Paweł i Piotrek spotkali się w pubie tuż po zdanym egzaminie z matematyki dyskretnej. Okazało się, że jest pięć marek piwa do wyboru. Na ile sposobów mogą oni wypić pierwszą kolejkę?
Każdy wybór marki piwa przez wszystkie osoby możemy interpretować jako funkcję ze zbioru w pięcioelementowy zbiór marek piwa. A więc istnieje sposobów spożycia pierwszej kolejki. I tyleż sposobów dla każdej nastepnej......
Przykład
Kod PIN jest kodem autoryzującym właściciela karty bankomatowej. Składa się on z cyfr dziesiętnych. Ile jest różnych kodów PIN?
Każdy kod PIN to funkcja z czteroelementowego zbioru pozycji w dziesięcioelementowy zbiór cyfr . Z Obserwacji 3.9 wynika że kodów PIN jest dokładnie .
Posługując się Obserwacją 3.8 udowodnimy jeszcze raz wzór na ilość podzbiorów skończonego zbioru. Zatem Obserwację 3.9 możemy traktować jako uogólnienie Obserwacji 3.8.
Dowód
Alternatywny dowód Obserwacji 3.8
Zauważmy, że dowolny podzbiór wyznacza jednoznacznie funkcję w następujący sposób:
Również każda funkcja wyznacza jednoznacznie podzbiór zbioru . Nadto, odpowiedniość
jest bijektywna. Zatem .
Obserwacja 3.10
Liczba injekcji ze zbioru skończonego w zbiór skończony wynosi:
Dowód
Niech i . Każdą injekcję z w możemy utożsamić z uporządkowanym wyborem różnych elementów ze zbioru :
Pierwszy element możemy wybrać na sposobów, drugi na , bo musi być różny od poprzednio wybranego, trzeci już tylko na sposoby, itd., aż wreszcie -ty na sposobów. Zatem liczba injekcji równa jest .
Przykład
Ile jest PIN-ów, czyli cztero-elementowych słów złożonych z cyfr dziesiętnych, takich że żadna cyfra się nie powtarza?
Każdy PIN z niepowtarzającymi się cyframi to injekcja z cztero-elementowego zbioru pozycji w -elementowy zbiór cyfr . Zatem jest ich dokładnie .
Obserwacja 3.11
Liczba bijekcji pomiędzy skończonymi zbiorami i , gdzie wynosi .
Dowód
Pokażemy najpierw, że każda injekcja jest bijekcją. Istotnie, gdyby nie było surjekcją, to byłoby właściwym podzbiorem zbioru . A zatem i funkcja ustalałaby injekcję ze zbioru o większej liczbie elementów w zbiór o mniej liczny. A to nie jest możliwe na mocy Obserwacji 3.3. Udowodniliśmy, że liczba bijekcji z w równa jest liczbie injekcji z w , czyli, z Obserwacji 3.10), wynosi ona:
Zauważmy jeszcze, że jest nie tylko funkcją , ale i bijekcją i jest to jedyna bijekcja .
Przykład
Na kurs tańca uczęszcza pięciu chłopaków i pięć dziewcząt. Większość kroków tanecznych ćwiczy się parami. Dla urozmaicenia pary często się zmieniają. Na ile sposobów może być wykonany jeden taniec?
Niech będzie zbiorem chłopaków, a zbiorem dziewcząt. Matematycznym modelem doboru par do tańca jest bijekcja . Zatem możliwych wyborów jest tyle samo co bijekcji pomiędzy -elementowymi zbiorami, czyli .
Permutacje
Permutacja zbioru skończonego to bijekcja z w .
Zbiór permutacji zbioru oznaczamy przez , a permutacje bedziemy w tym kursie oznaczać małymi literami greckimi.
Przykład
Rozważ funkcję zadaną przez poniższą tabelę:
Funkcja jest bijekcją z w , zatem jest permutacją i .
Przykład
Dla permutacji zadanych przez poniższą tabelę:
ich złożenia podane są poniżej:
Zauważ, że oba złożenia także są permutacjami .
Ponieważ permutacje są bijekcjami, to natychmiast z Obserwacji 3.2 dostajemy:
Obserwacja 3.12
Dla dowolnych permutacji skończonego zbioru :
- są permutacjami ,
- jest permutacją taką, że .
Następne spostrzeżenie jest natychmiastowym wnioskiem z Obserwacji 3.11.
Wniosek 3.13
Zbiór -elementowy ma dokładnie permutacji, .
Przykład
Oto wszystkie () permutacje zbioru :
Permutację zbioru wygodnie jest identyfikować z krotką . Często też permutację interpretuje się jako uporządkowanie zbioru .

Przykład
Na ile sposobów można poukładać koło siebie na półce książek?
Na dokładnie tyle, ile jest permutacji zbioru siedmio-elementowego, a więc .
Cykl zbioru -elementowego to taka permutacja zbioru , dla której , przy dowolnym . Łatwo zauważyć, że jeśli dla pewnego mamy , to jest tak dla wszystkich , czyli jest cyklem na . Cykl zbioru zapisujemy jako dla dowolnie wybranego .
Przykład
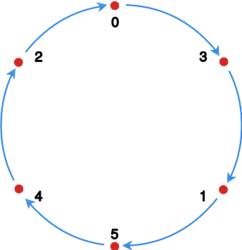
Rozważmy daną przez
- sekwencja , , , , , pokwywa całe ,
- zatem jest cyklem.
Rozkład permutacji na rozłączne cykle
Dowolną permutację zbioru można rozłożyć na rozłączne cykle w sposób następujący:
- wybierz dowolny element , który nie jest jeszcze w żadnym cyklu,
- iteruj permutację otrzymując kolejno: aż do uzyskania ,
- dodaj do rozkładu cykl ,
- jeśli w zbiorze pozostały jeszcze elementy niepokryte przez żaden cykl, to wróć do pierwszego punktu.
Dowód
Dla dowodu poprawności algorytmu rozkładu pokażemy najpierw, że iteracja w drugim punkcie zawsze osiąga element wyjściowy . Ponieważ zbiór jest skończony iteracja w pewnym kroku musi wrócić do elementu już rozważanego, zatem dla pewnych . Weźmy najmniejsze takie , że dla pewnego . Gdyby to z faktu, że jest permutacją mamy , co stoi w sprzeczności z minimalnością . A zatem .
Pozostaje jeszcze pokazać, że otrzymane cykle są rozłączne. Załóżmy, że nie są i weźmy pierwszy napotkany element , który był już w którymś z poprzednich cykli. Zauważmy, że gdyż był wybrany jako element nie pokryty przez żaden cykl (patrz punkt pierwszy). Wiemy, że istnieje element w tym samym cyklu co taki, że , ale także . Ponieważ jest permutacją, otrzymujemy , co stoi w sprzeczności z faktem, że jest jedynym elementem z poprzedniego cyklu.
Jeśli permutacja złożona jest z rozłącznych cykli, to zapisujemy , gdzie w kolejnych nawiasach są elementy kolejnych cykli startujące od odpowiednio: .
Przykład
Rozważmy jeszcze raz permutację :
Rozkład na cykle:
- , , , , , , ,
- , ,
- .