TC Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ </math>” na „</math>” |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| Linia 146: | Linia 146: | ||
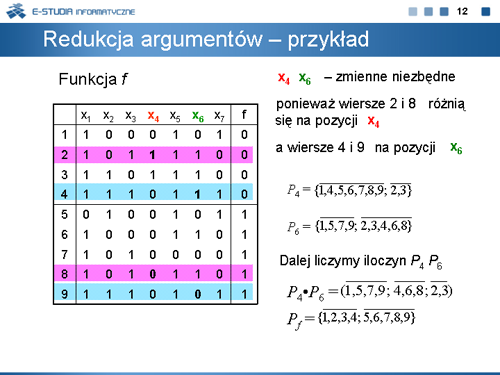
|valign="top"|Iloczyn podziałów wyznaczonych przez zmienne niezbędne ma bardzo ważną interpretację. | |valign="top"|Iloczyn podziałów wyznaczonych przez zmienne niezbędne ma bardzo ważną interpretację. | ||
Zauważmy, że kolejne bloki iloczynu <math>P = (B_1, | Zauważmy, że kolejne bloki iloczynu <math>P = (B_1,\ldots,B_3)\,</math> są <math>B_1=\left \{1,5,7,9 \right \}</math> , <math>B_2=\left \{4,6,8\right \}</math> , <math>B_3 = {2,3\}</math>.Blok <math>B_3\,</math> jest zawarty w jednym bloku podziału <math>P_f\,</math>. Ale bloki <math>B_1\,</math> i <math>B_2\,</math> zawierają elementy należące do dwóch różnych bloków podziału <math>P_f\,</math>, czyli same zmienne <math>x_4\,</math> , <math>x_6\,</math> nie wystarczają do oddzielenia wektorów prawdziwych od fałszywych realizowanej funkcji. | ||
|} | |} | ||
Aktualna wersja na dzień 21:58, 15 wrz 2023

|
Redukcja argumentów |
|
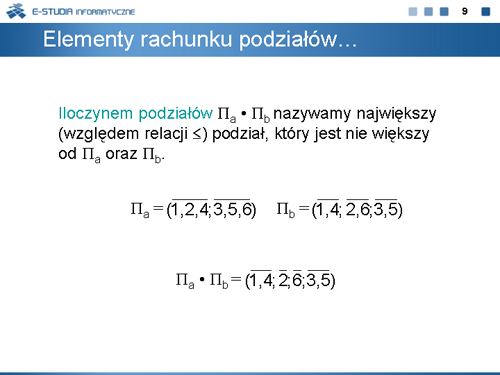
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|
Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący:
|

|
Porównajmy wyniki tak przeprowadzanych minimalizacji.
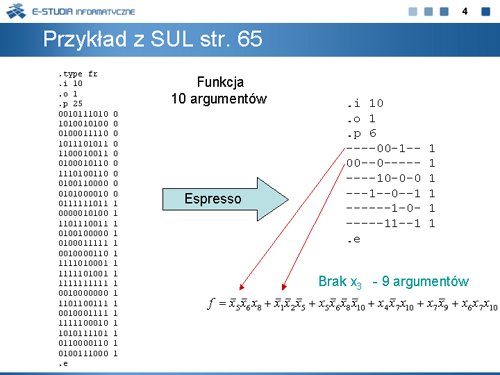
Wynik Espresso – 9 argumentów, 6 termów
Wynik Pandora – 7 argumentów, 5 termów
|

|
Możemy więc porównać wynik minimalizacji programem Espresso:
z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów.
|
</math>