PF Moduł 10

Wykład

Wprowadzenie Termodynamika statystyczna opisuje układy wielu cząsteczek, z jakich składają się ciała za pomocą wielkości średnich (średnia prędkość, średnia droga, średnia energia itd.) oraz tzw. rozkładów statystycznych. Wiąże mikroskopowe, dane statystyczne o cząsteczkach z makroskopowymi parametrami stanu. Posługuje się rachunkiem prawdopodobieństwa i pozwala wyznaczać najbardziej prawdopodobne kierunki procesów.

---

Pomimo, że Identyczne cząsteczki są w chaotycznym ruchu Wszystkie kierunki ich ruchu są jednakowo prawdopodobne Temperatura jest miarą ich średniej energii kinetycznej Prędkości zmieniają się w wyniku zderzeń Prędkości poszczególnych cząsteczek są różne w szerokim zakresie wartości. To Rozkład Maxwella opisuje prędkości cząsteczek gazu doskonałego będącego w stanie równowagi termodynamicznej, na który nie działają siły zewnętrzne. Pozwala obliczyć charakterystyczne wartości wielkości średnich: średnią prędkość kwadratową, średnią prędkość i prędkość najbardziej prawdopodobną oraz liczbę cząsteczek o prędkościach zawartych w przedziale wartości od $v$, do $v+dv$,. Jeżeli mamy $N$, cząsteczek, to liczba $d{N}_v$, cząsteczek o prędkościach w przedziale od $v$, do $v+dv$, będzie określona wzorem $d{N}_v=N\cdot F(v)\cdot dv$ , gdzie $F(v)$, dane jest wzorem $F(v)={\left(\frac{m_0}{2\cdot \pi \cdot k\cdot T}\right)}^{3/2}\cdot exp(-\frac{m_0\cdot v^2}{2\cdot k\cdot T})\cdot 4\cdot \pi \cdot v^2$

---

Wyprowadzenie wzoru można znaleźć w literaturze. $F(v)={\left(\frac{m_0}{2\cdot \pi \cdot k\cdot T}\right)}^{3/2}\cdot exp(-\frac{m_0\cdot v^2}{2\cdot k\cdot T})\cdot 4\cdot \pi \cdot v^2$ Co jest charakterystyczne w tym rozkładzie $F(v)$, ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od $v$, . (Przeanalizuj dokładnie trzy człony wzoru na $F(v)$, . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla $v=0$, , ostatni - rosnący paraboliczne ze wzrostem prędkości. Rezultat jest zobrazowany na wykresie maxwellowskiej funkcji rozkładu prędkości cząsteczek azotu przy temperaturach: $73K(-200^{\circ }C)$, , $273K(0^{\circ }C)$, , $473K(200^{\circ }C)$,. Gdy temperatura rośnie maksimum krzywej rozkładu przesuwa się w stronę większych prędkości i krzywa ulega spłaszczeniu. Pole pod krzywą równe jest całkowitej liczbie cząsteczek w próbce i pozostaje stałe niezależnie od temperatury. Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach.

---

Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, $v_p$, . Można ją określić z matematycznego warunku na maksimum funkcji. $\frac{dF(v)}{dv}{|}_{v=v_p}=0$ Stąd otrzymuje się $v_p=\sqrt{2\cdot k\cdot T/m_0}$ , a więc $v_p<v_{sr.kw.}$ jak to wynika z definicji średniej prędkości kwadratowej (teoria kinetyczna). Korzystając z funkcji rozkładu można obliczyć odpowiednio prędkość średnią (średnia arytmetyczną wszystkich prędkości)

---

]

Ciśnienie atmosferyczne w danym punkcie nad powierzchnią Ziemi określone jest przez ciężar warstwy powietrza leżącej powyżej tego punktu, powinno zależeć od wysokości. Im większa wysokość, tym mniejsza jest warstwa powietrza, więc i ciśnienie jest mniejsze. Różnica ciśnień $dp$, związana ze wzrostem wysokości $dh$, ma znak ujemny i wynosi $dp=-\rho \cdot g\cdot dh$ gdzie $\rho$, jest gęstością gazu na wysokości $h$, , a $g$, jest przyspieszeniem ziemskim na tej wysokości. Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola $p\cdot V=R\cdot T$ przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy $p\cdot \begin{array}{c}\underbrace{(V/M)}\\ 1/\rho \end{array}=\frac{R\cdot T}{M}$ , czyli $\rho =\frac{M\cdot p}{R\cdot T}$ Więc możemy napisać, że $dp=-\frac{M\cdot p\cdot g}{R\cdot T}\cdot dh$ Otrzymujemy w ten sposób równanie różniczkowe o rozdzielonych zmiennych $\frac{dp}{p}=-\frac{M\cdot g}{R\cdot T}\cdot dh$ Zakładając, że temperatura atmosfery ma wartość stałą (tzw. atmosfera izotermiczna) i pole grawitacyjne jest jednorodne $(g(h)=const)$, możemy łatwo scałkować to równanie otrzymując $lnp=-\frac{M\cdot g\cdot h}{R\cdot T}+lnC$ gdzie $lnC$, to stała całkowania. Wynika stąd, że $p=C\cdot exp(-\frac{M\cdot g\cdot h}{R\cdot T})$ Dla $h=0$, ciśnienie równe jest ciśnieniu atmosferycznemu $p_0$, na powierzchni Ziemi. Stąd wyznaczamy stałą, $C=p_0$, . Ostatecznie otrzymujemy $p=p_0\cdot exp(-\frac{M\cdot g\cdot h}{R\cdot T})$ Jest to tzw. wzór barometryczny. Wynika z niego, że ciśnienie zmienia się z wysokością szybciej dla niższych temperatur oraz dla cięższego gazu, i że zmiana ta ma charakter wykładniczy Wzór barometryczny obowiązuje dla atmosfery izotermicznej, dla której mamy oraz jednorodnego pola grawitacyjnego. Jeżeli warunki te nie są spełnione, należy odpowiednio podstawić zależność funkcyjną temperatury od wysokości oraz zależność $g=g(h)$, i rozwiązać otrzymane równanie różniczkowe. Korzystając z faktu, że $\frac{M}{R}=\frac{N_A\cdot m_0}{N_A\cdot k}=\frac{m_0}{k}$ , gdzie $m_0$, - średnia masa cząsteczki powietrza, możemy wzór barometryczny przedstawić w postaci $p=p_0\cdot exp(-\frac{m_0\cdot g\cdot h}{k\cdot T})$

---

]

W rozważaniach dotyczących rozkładu Maxwella ignorowaliśmy całkowicie fakt, że cząsteczki poruszają się w polu sił ciężkości, a więc wyróżniony jest kierunek pionowy. Wzór barometryczny wskazuje, że ciężar cząsteczek ma wpływ na rozkład ciśnienia w funkcji wysokości. Jak uwzględnić ten efekt w opisie rozkładu prędkości cząsteczek? Przepiszmy w nieco innej formie wzór barometryczny. Zakładając atmosferę izotermiczną, możemy zamienić ciśnienia $p$, i $p_0$, występujące we wzorze barometrycznym wielkościami $n$, i $n_0$, , które reprezentują koncentrację cząsteczek, czyli ich liczbę w jednostce objętości na wysokości $h$, oraz na powierzchni Ziemi. Wykorzystując to zapiszemy wzór barometryczny w formie $n=n_0\cdot exp(-\frac{m_0\cdot g\cdot h}{k\cdot T})$ Zwróćmy uwagę, że wyrażenie $m_0\cdot g\cdot h$, jest po prostu energią potencjalną $E_p$, cząsteczki w polu sił ciężkości (przy założeniu jednorodnego pola grawitacyjnego). Więc również $n=n_0\cdot exp(-\frac{E_p}{k\cdot T})$ Ten wzór wyraża zależność koncentracji cząsteczek od ich wysokości lub grawitacyjnej energii potencjalnej. Wynikający z niego rozkład koncentracji nosi nazwę rozkładu Boltzmanna i odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym.

---

Stan układu określany przez parametry makroskopowe, jak temperatura, ciśnienie, energia wewnętrzna, itd. nazywamy makrostanem. Stan układu wyznaczony przez określenie stanów wszystkich cząsteczek wchodzących w jego skład nazywamy mikrostanem. Liczba możliwych mikrostanów odpowiadających danemu makrostanowi jest na ogół ogromna, analiza nasza będzie mieć charakter statystyczny. Liczba mikrostanów odpowiadających danemu makrostanowi nazywa się prawdopodobieństwem termodynamicznym lub wagą statystyczną makrostanu. Rozpatrzmy sens wagi statystycznej na przykładzie naczynia z gazem, w którym znajduje się $N$, cząsteczek. Stan danej cząsteczki opiszemy tylko jedną informacją - w której części naczynia, lewej czy prawej, cząsteczka się znajduje. Zbiór tych informacji dla wszystkich $N$, cząsteczek określa mikrostan naszego układu. (Dla uproszczenia rozważań nie będziemy brać pod uwagę prędkości, kierunku ruchu, masy cząsteczek itp.). Makrostan układu określamy podając sumaryczną liczbę cząsteczek z jednej (np. lewej) strony naczynia. Nie bierzemy tu pod uwagę prędkości cząsteczek, ale makroskopowy parametr jakim jest ciśnienie gazu zależne od jego gęstości, a gęstość proporcjonalna jest do liczby cząsteczek w jednostce objętości. Liczba makrostanów, to liczba przypadków, w których $k$, cząsteczek (nie ważne których) znajduje się z lewej strony oraz $N-k$, , z prawej strony. Liczba mikrostanów dla danego makrostanu, w którym $k$, cząsteczek znajduje się z lewej strony równa jest liczbie kombinacji $k$, - elementowych w zbiorze o $N$, elementach i wynosi $W$,.

---

Dla zilustrowania tych relacji przeanalizujmy szczegółowo przypadek małej liczby cząsteczek, na przykład - czterech. W lewej kolumnie tabeli wymienione są możliwe makrostany układu. Wszystkie możliwe mikrostany odpowiadające danemu makrostanowi wymienione są w kolejnej kolumnie. Podane są tam wszystkie sposoby, na jakie może być realizowany dany makrostan. W następnej kolumnie znajdują się liczby mikrostanów odpowiadających danemu makrostanowi, czyli wagi statystyczne poszczególnych makrostanów. W kolumnie z prawej strony podane są prawdopodobieństwa realizacji poszczególnych makrostanów. Na dole tablicy podana jest sumaryczna liczba mikrostanów oraz sumaryczne prawdopodobieństwo, które równe jest, oczywiście, jedności. Zakładamy, że cząsteczki są rozróżnialne (tzn. możemy je np. ponumerować). Liczba mikrostanów dla danego makrostanu, w którym $k$, cząsteczek znajduje się z lewej strony równa jest liczbie kombinacji $k$, - elementowych w zbiorze o $N$, elementach i wynosi $W(N,k)=\frac{N!}{k!(N-k)!}$ Jest to właśnie waga statystyczna danego makrostanu. Sumaryczna liczba wszystkich mikrostanów wynosi $2^N$,. Prawdopodobieństwo danego makrostanu jest równe stosunkowi jego wagi statystycznej do sumarycznej liczby wszystkich mikrostanów i dla naszego przypadku podane jest w prawej kolumnie tabeli. Prawdopodobieństwo, że dana cząsteczka znajdzie się z prawej lub z lewej strony naczynia jest takie samo, czyli prawdopodobieństwa wszystkich mikrostanów są sobie równe. Uogólnienie tego stwierdzenia na zdefiniowane w dowolny sposób mikrostany nosi nazwę hipotezy ergodycznej.

---

Najbardziej prawdopodobne są makrostany, w których po obu stronach znajduje się ta sama liczba cząsteczek. Gdybyśmy w stanie początkowym umieścili gaz z jednej strony naczynia, to po pewnym czasie cząsteczki zajęłyby pozycje odpowiadające największej wadze statystycznej, czyli największemu prawdopodobieństwu termodynamicznemu. Stan taki nazywamy stanem równowagi. Układ wyprowadzony ze stanu równowagi ma tendencję do samorzutnego powrotu do tego stanu. Inne stany układu są mniej prawdopodobne. Proces zmierzający do ustalenia się w układzie stanu równowagi jest procesem nieodwracalnym, bowiem proces do niego odwrotny jest bardzo mało prawdopodobny. Możemy wiec powiedzieć, że dany proces jest wtedy nieodwracalny, gdy proces do niego odwrotny jest bardzo mało prawdopodobny.

---

Kiedy układ składa się z nie oddziałujących podukładów wówczas prawdopodobieństwo stanu równe jest iloczynowi prawdopodobieństw stanów podukładów. $W=W_1\cdot W_2$ Stan układu, oprócz znanych nam już parametrów jak temperatura, czy ciśnienie można także scharakteryzować przez inną wielkość zawierająca informacje o jego prawdopodobieństwie termodynamicznym. Wielkością taką jest entropia zdefiniowana poprzez logarytm naturalny z prawdopodobieństwa termodynamicznego. Dzięki takiej definicji entropia układu jest sumą entropii podukładów, bowiem iloczyn prawdopodobieństw zamienia się w sumę ich logarytmów. $lnW=ln{W}_1\cdot ln{W}_2$ Jak wiemy, entropię można także zdefiniować poprzez wielkości makroskopowe. Definicja entropii łącząca jej cechy mikroskopowe i makroskopowe oraz określająca jej sens statystyczny ma postać $S=k\cdot lnW$ gdzie $k$, jest znaną nam już stałą Boltzmanna. Entropia rośnie wraz ze wzrostem prawdopodobieństwa stanu układu, jest logarytmiczną miarą tego prawdopodobieństwa.

---

Wymieńmy podstawowe własności entropii wynikające z naszych wcześniejszych rozważań. 1. Przemiany nieodwracalne zachodzące w układzie izolowanym prowadzą do wzrostu entropii układu. Prawo to wyraża wzór $dS>0$, . Przykładem może być rozważany przez nas układ podzielony umownie na część lewą i prawą. Wzrost prawdopodobieństwa statystycznego równoważny jest ze wzrostem entropii tego układu. Prawo wzrostu entropii ma charakter ogólny i odnosi się do wszelkich procesów zachodzących w przyrodzie. Wzrost entropii równoznaczny jest ze wzrostem nieuporządkowania elementów układu; z przechodzeniem ich od stanu uporządkowanego do stanu chaotycznego. Stanem pewnego uporządkowania jest zgromadzenie gazu w jednej części naczynia, ale także stanem uporządkowania jest półka z ustawionymi na niej książkami. Kiedy półka spada i w rezultacie książki są porozrzucane na podłodze, mamy także do czynienia za wzrostem entropii układu. To samo dotyczy rozbitej szklanki, która spadła ze stołu, zburzonych w wyniku trzęsienia Ziemi domów, wracającej do położenia równowagi drgającej sprężyny itd. 2. W stanie równowagi entropia układu osiąga wartość maksymalną. Kiedy w wyniku przemiany nieodwracalnej układ zwiększa swą entropię, to stan jego równowagi równoznaczny jest z maksymalną wartością entropii układu.

---

Materiały do ćwiczeń

Zadanie 10.3

Oblicz zmianę entropii $n_M$, moli gazu doskonałego w procesie izotermicznego rozprężania od objętości $V_0$, do objętości $V_k$,

Rozwiązanie

Układem jest porcja $n_M$, moli gazu zawierająca liczbę $N$, identycznych, niezależnych cząsteczek (podukładów). Prawdopodobieństwo stanu $W$, równe jest iloczynowi prawdopodobieństw stanów podukładów $w_i(1,2,\dots ,N)$,.

Dla pojedynczej cząsteczki prawdopodobieństwo jej przebycia w objętości $V$, jest proporcjonalne do $V$,, a dla $N$, cząsteczek do $V^n$,. Więc $w_i=A\cdot V$

$W=w_i^N=(A\cdot V{)}^N$ A jest stałą proporcjonalności. Z definicji entropii, będzie:

$S=k\cdot N(lnA+lnV)$

Liczba cząsteczek i ich temperatura nie zmienia się. Zwiększa się objętość porcji gazu od $V_0$, do $V_k$, i zwiększa się entropia (nieuporządkowanie) układu

$\mathrm{\Delta }S=S_k-S_0=k\cdot N(lnA+ln{V}_k)-k\cdot N(lnA+ln{V}_0)=k\cdot N\cdot ln\frac{V_k}{V_0}=n_M\cdot R\cdot ln\frac{V_k}{V_0}$

---

Zadanie 10.4

Przy jakiej temperaturze średnia prędkość kwadratowa cząsteczek dwutlenku węgla będzie równa średniej prędkości kwadratowej cząsteczek azotu w temperaturze $0^{\circ }C$?

Odpowiedź

Przy temperaturze $429K$,.

---

Zadanie 10.5

Izolowany układ dwóch zbiorników. Zbiornik o objętości $V_1$, zawierał $n_{M1}$, moli gazu o temperaturze $T$, . Zbiornik o objętości $V_2$, zawierał $n_{M2}$, moli również o temperaturze $T$, , Oblicz zmianę entropii tych gazów po połączeniu zbiorników i powstaniu mieszaniny.

Odpowiedź

$\mathrm{\Delta }S=R\cdot (n_{M1}\cdot ln\frac{V_1+V_2}{V_1}+n_{M2}\cdot ln\frac{V_1+V_2}{V_1})$ , entropia układu wzrośnie, bo jest to proces nieodwracalny, entropia układu wzrośnie, bo wzrośnie nieuporządkowanie elementów układu.

---

Słowniczek

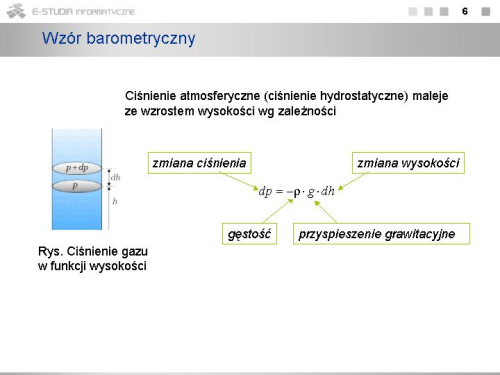
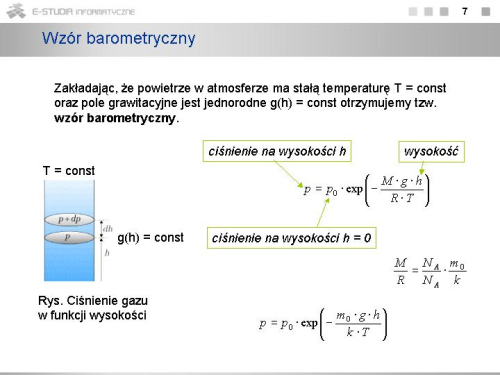
wzór barometryczny	podaje zależność ciśnienia atmosferycznego od wysokości nad powierzchnią Ziemi
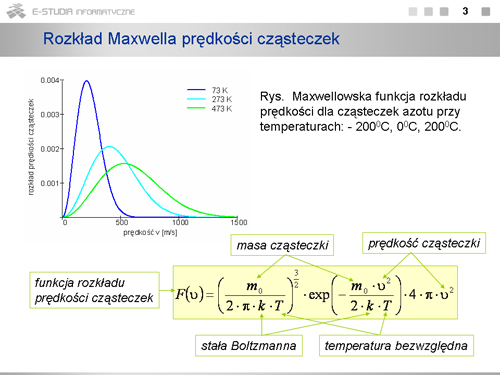
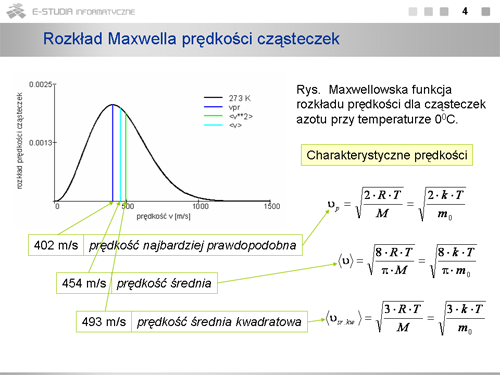
rozkład Maxwella prędkości cząsteczek	rozkład wartości prędkości chaotycznego ruchu cząsteczek gazu doskonałego dla zadanej temperatury i masy cząsteczek
rozkład Boltzmanna	rozkład koncentracji cząsteczek w funkcji ich wysokości lub energii potencjalnej. Odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym.
mikrostan	stan układu w którym opisane są stany wszystkich jego elementów
hipoteza ergodyczna	Prawdopodobieństwa wszystkich mikrostanów są jednakowe
makrostan	stan układu opisany za pomocą wielkości odnoszących się do całości układu
prawdopodobieństwo termodynamiczne (waga statystyczna)	odnosi się do makrostanu układu: liczba mikroskoopowych sposobów realizacji danego makrostanu (liczba mikrostanów odpowiadająca danemu makrostanowi)
entropia	definicja statystyczna: wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu
fluktuacje	losowe odchylenia danej wielkości od wartości średniej
prawo wzrostu entropii	entropia układu izolowanego nie może maleć, w procesach nieodwracalnych entropia układu rośnie

---