PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 722: | Linia 722: | ||
Zadanie 8.2 | ''Zadanie 8.2'' | ||
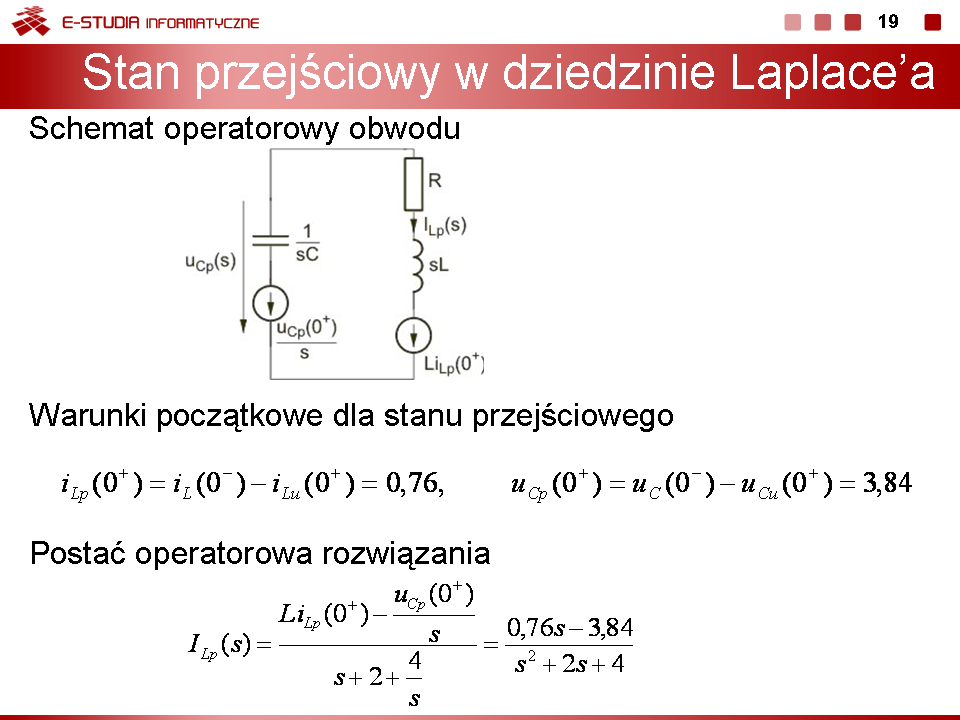
Określić przebieg napięcia na kondensatorze w stanie nieustalonym po przełączeniu metodą operatorową w obwodzie przedstawionym na rys. poniższym. Przyjąć następujące parametry obwodu:<math>R_1=50\Omega</math>, <math>R_2=100\Omega</math>, <math>C_1=10\mu F</math>, <math>C_2=20\mu F</math>, <math>e_1(t)=50V</math>, <math>e_2(t)=100V</math>. | Określić przebieg napięcia na kondensatorze w stanie nieustalonym po przełączeniu metodą operatorową w obwodzie przedstawionym na rys. poniższym. Przyjąć następujące parametry obwodu:<math>R_1=50\Omega</math>, <math>R_2=100\Omega</math>, <math>C_1=10\mu F</math>, <math>C_2=20\mu F</math>, <math>e_1(t)=50V</math>, <math>e_2(t)=100V</math>. | ||
| Linia 729: | Linia 729: | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt2.jpg]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt2.jpg]] | ||
|} | |} | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
| Linia 739: | Linia 740: | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt3.jpg]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt3.jpg]] | ||
|} | |} | ||
Z metody potencjałów węzłowych zastosowanych do obwodu z rys. 9.18 wynika | |||
<math>U_C(s)=\frac{\frac{50}{50s}+\frac{100}{100s}+10^{-5}u_{C1}(0^{+})+2 \cdot 10^{-5}u_{C2}(0^{+})}{1/50+1/100+s10^{-5}+2s10^{-5}}</math> | |||
<math>U_C(s)=\frac{250s+2,5\cdot 10^{-5}}{3s(s+1000)}</math> | |||
Bieguny układu: <math>s_1=0</math>, <math>s_2=1000</math> | |||
Transformata odwrotna Laplace’a | |||
: <math>u_C(t)=\lim_{s \to 0} {U_C(s)se^{st}}+\lim_{s \to 1000} {U_C(s)(s+1000)e^{st}}</math> | |||
: <math>u_C(t)=\frac{250}{3}+\frac{50}{3}e^{-1000t}</math> | |||
W stanie ustalonym przy <math>t \to \infty</math> mamy <math>u_{Cu}(t)=\frac{250}{3} V</math>. Zauważmy, że w wyniku przełączenia napięcia na kondensatorach w chwili t=0 uległy skokowej zmianie (w obwodzie powstało oczko złożone z samych kondensatorów). | |||
''Zadanie 8.3'' | |||
Wartości indukcyjności i pojemności w obwodzie szeregowym RLC są równe: <math>L=0,01H</math> oraz <math>C=1\mu F</math>. Określić zmiany częstotliwości drgań własnych tego obwodu w funkcji wartości rezystancji R zmieniającej się od zera do rezystancji krytycznej. | |||
''Rozwiązanie'' | |||
Częstotliwość drgań własnych obwodu szeregowego RLC dana jest wzorem | |||
: <math>f=\frac{1}{2\pi}\sqrt {\frac{1}{LC}-\frac{R^2}{4L^2}}=\frac{1}{2\pi}\sqrt{10^8-0,25\cdot 10^4 R^2}</math> | |||
Rezystancja krytyczna | |||
: <math>R_{kr}=2\sqrt{\frac{L}{C}}=200\Omega</math> | |||
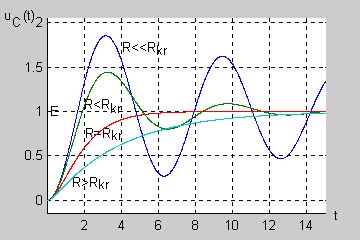
Na rys. ponizszym przedstawiono zależność częstotliwości drgań własnych obwodu od wartości rezystancji R w podanym zakresie zmian rezystancji | |||
Wersja z 05:02, 2 sie 2006

|
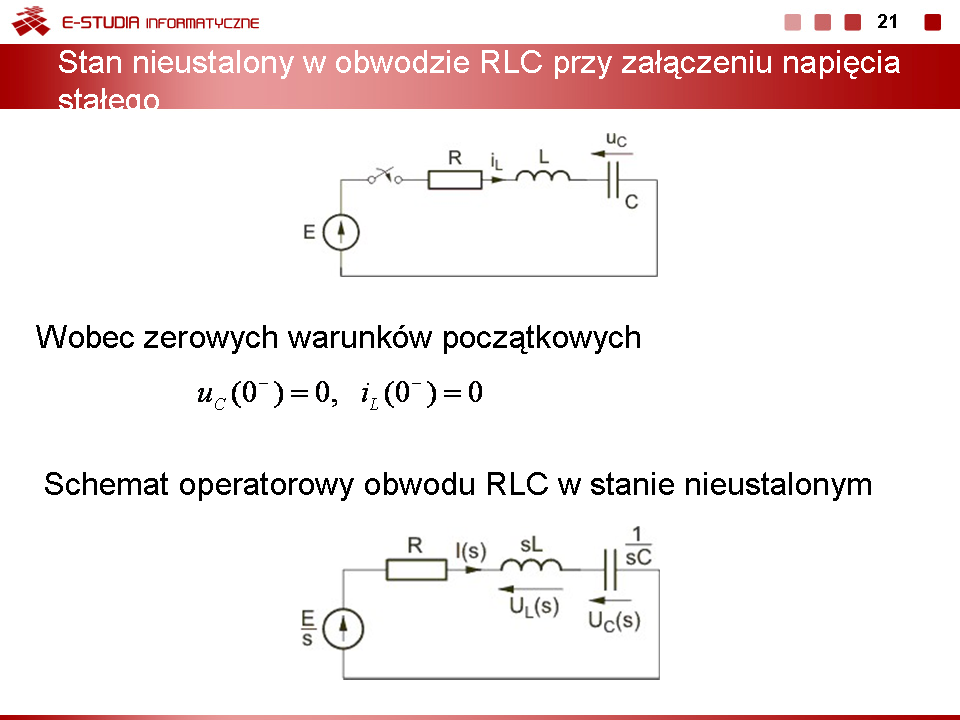
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |